Feladat: F.1694 Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1970/november, 118 - 119. oldal  PDF  |  MathML 
Témakör(ök): Térgeometriai bizonyítások, Tetraéderek, Feladat
Hivatkozás(ok):Feladatok: 1969/december: F.1694

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. 1. Megmutatjuk, hogy a föltétel szerinti tetraéder mindegyik éle merőleges a vele szemben levő élre. Elég ezt az ABCD tetraédernek pl. DA, BC élpárjára bizonyítani, mert a kiemelt csúcs ‐ legyen pl. D ‐ mindhárom élpár egyik tagjának végpontja, a vele szemben fekvő lap pedig ‐ most az ABC lap ‐ tartalmazza mindegyik élpár egyik tagját.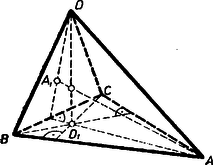
Legyen D-nek az ABC lapon levő vetülete, egyben ennek a lapháromszögnek magasságpontja, D1. Az utóbbi tulajdonság miatt AD1 merőleges BC-re, az előbbi miatt pedig DD1, hiszen ha DD1 merőleges az ABC lap síkjára, akkor merőleges ennek minden egyenesére, köztük BC-re is. Így tehát merőleges BC-re a mondott két egyenes által meghatározott DD1A sík is, és vele DA egyenese is, amint állítottuk (1. ábra).

 
 
1. ábra
 

Indokolásunk nem helyes akkor, ha D1 egybeesik A-val (vagyis az alapháromszög A-nál derékszögű), mert ekkor D, D1 és A nem határoz meg síkot (2. ábra).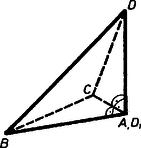
 
 
2. ábra
 

Állításunk azonban ekkor is helyes, sőt nyilvánvaló, hiszen ekkor már maga a DA él merőleges az ABC síkra. (A DA egyenes már nem határozatlan, D≠A, különben nem lehetne beszélni gúláról.)
2. A feladat állítását is elég lesz most már egyetlen, a D-től különböző csúcsra bizonyítani, legyen ez A, és vetülete a BCD lapháromszög síkján A1 (1. ábra). Eszerint az AA1 egyenes, a bebizonyított segédtétel szerint pedig az AD él merőleges a BC élre, így az általuk meghatározott AA1D sík minden egyenese, köztük DA1 is. Eszerint A1 rajta van a BCD háromszög D-ből induló magasságegyenesén.
Ugyanígy, D helyén pl. B-t véve, AB és AA, merőlegesek CD-re, ezért BA1 is, így A1 rajta van az ABC háromszög B-ből induló magasságegyenesén is, ekkor pedig magasságpontja a BCD háromszögnek.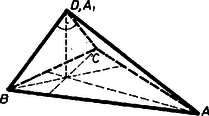
 
 
3. ábra
 

Amennyiben az ezen meggondolásunk első vagy második részében fölhasznált sík és egyenes nem volna határozott, pl. az első részben az AA1D sík és a DA1 egyenes határozatlan volna, mert A1 egybeesik D-vel (3. ábra), akkor a meggondolás másik ‐ a példát folytatva a második ‐ része biztosan érvényes, hiszen A, nem eshet egybe D-vel is és B-vel is, és a ,,DC⊥BA1'' megállapítás így alakul: CD⊥BD, vagyis a BCD háromszög D-nél derékszögű. Így pedig magasságpontja maga D, azaz A1.
 

Megjegyzés. Az 1. ábra esetében ‐ ha ti. D1 nem esik egybe az ABC háromszög egyik csúcsával sem, akkor ‐ a tetraéder DD1, AA1 magasságvonalai mint a DD1A sík egyenesei, metszik egymást, és ez érvényes bármely két magasságra, tehát a tetraéder 4 magasságvonala egy pontban metszi egymást (ortocentrikus, azaz magasságponttal bíró tetraéder, más néven normáltetraéder). A 2. ábrán A, a 3. ábrán D a magasságpont ‐ a két eset lényegében azonos ‐ és 3 lap derékszögű háromszög. (A tetraéder magasságvonalai általában nem metszik egymást.)
 

II. megoldás. Első lépésként bebizonyítjuk a következő segédállítást: az ABCD tetraéder D csúcsának az ABC lapon levő D1 vetülete akkor és csakis akkor van az ABC lap C csúcsához tartozó mc, magasságvonalán, ha AB⊥ ⊥CD.
a) Ha AB⊥CD, akkor a CD és mc egyenesek által meghatározott S sík merőleges AB-re, hiszen e sík két meghatározó egyenese AB-re merőleges (4. ábra).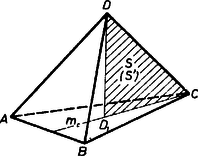
 
 
4. ábra
 

(E két egyenes különböző, mert mc, benne van az ABC síkban, CD viszont nincs benne.) AB tehát merőleges az S sík minden egyenesére. Legyen D* a D pont vetülete az mc egyenesen, ekkor DD*⊥AB. Viszont DD* merőleges mc-re is, tehát ez az egyenes merőleges az ABC sík két (egymástól különböző) egyenesére, így merőleges az ABC síkra is, vagyis D* azonos D1-gyel, más szóval D1 rajta van mc-n.
b) Fordítva, ha D1 rajta van mc-n, akkor a DD1mc egyenesek által meghatározott S' merőleges AB-re, hiszen DD1 merőleges az ABC sík minden egyenesére, így AB-re is, és nyilván mc⊥AB. (mc és DD1, különbözők, mert mc benne van az ABC síkban, DD1 pedig nincs benne.) Az AB egyenes tehát merőleges S' minden egyenesére, így CD-re is. Ezt akartuk bizonyítani. Ha mármost a tetraéder egyik csúcsának a szemközti lapon levő vetülete e lap magasságpontja, vagyis e lap mindhárom magasságvonalán rajta van, akkor segédállításunk b) része szerint ‐ a betűzést értelemszerűen változtatva ‐ a tetraédernek mind a három szemközti (kitérő) élpárja merőleges egymásra. Így pedig ‐ segédállításunk a) része szerint ‐ tetszőleges csúcsának a szemközti lapon levő vetülete rajta van e lap mindhárom magasságvonalán, tehát azonos e lap magasságpontjával.