Kezdőlap


Feladat:	F.1693	Korcsoport: 14-15	Nehézségi fok: nehéz
Megoldó(k):	Hima Tamás , Prőhle Tamás , Szabados György , Szokoli István
Füzet:	1970/október, 55 - 56. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Középpontos és egyéb hasonlósági transzformációk, Egyenlő szárú háromszögek geometriája, Húrnégyszögek, Síkgeometriai szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 1969/december: F.1693

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Megmutatjuk, hogy az analóg feladat két kör esetén is megoldható: ha adott két érintkező kör, $k_{1}$ és $k_{2}$ , és érintkezési pontjuk $T$ , akkor megszerkeszthetünk egy olyan egyenest, amelyik átmegy $k_{2}$ középpontján, $O_{2}$ .
Felhasználjuk, hogy $k_{1}$ és $k_{2}$ centrálisan hasonló helyzetűek $T$ -re mint középpontra vonatkozóan.
Olyan $s$ segédegyenesből indulunk ki, amely $k_{1}$ -et és $k_{2}$ -t az egymástól különböző $A_{1}$ , $B_{1}$ , $C_{2}$ , $D_{2}$ pontokban metszi, ebben a sorrendben. Messe a $T A_{1}$ , $T B_{1}$ egyenes $k_{2}$ -t az $A_{2}$ , ill. $B_{2}$ pontban. Ezek $s$ megválasztása folytán egymástól különbözők és az $A_{2} B_{2}$ húr az $A_{1} B_{1}$ húr megfelelője, tehát párhuzamosak. Így pedig az $A_{2} B_{2} C_{2} D_{2}$ négyszög húrtrapéz $k_{2}$ -ben, szárainak $E$ és átlóinak $F$ metszéspontját összekötve $k_{2}$ -nek $s$ -re merőleges átmárőegyenesét kapjuk (1. ábra).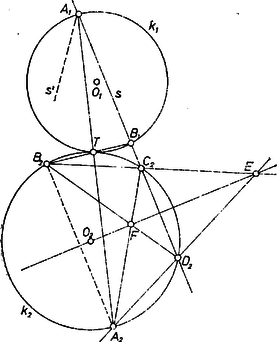

1. ábra

Egy, az

s

-sel nem párhuzamos

s'

-ből kiindulva az új átmérőegyenes metszi az előbbit a keresett

O_{2}

-ben. (Célszerű

s'

-t is pl.

A_{1}

-en át fölvenni, így a megismétlésben

A_{2}

ismét felhasználható.)
Az olvasóra hagyjuk annak átgondolását, hogy a felhasznált húrtrapéz szárai az

s

-nek csak különleges megválasztása esetében adódnának párhuzamosnak, ennélfogva

E

általában létrejön.

Prőhle Tamás (Budapest, Fazekas M. Gyak. Gimn., IV. o. t.)

II. megoldás. Legyen a három kör

k_{1}

k_{2}

k_{3}

, és

k_{1}

és

k_{2}

érintkezési pontja

T_{3}

k_{2}

és

k_{3}

-é

T_{1}

k_{3}

és

k_{1}

-é

T_{2}

. Ezek különböző pontok, mert kettő egybeesése esetén a harmadik körpár is ugyanott érintené egymást, ekkor pedig legalább egyik kör belülről érintene egy másikat. Ugyanezért az sem lehet, hogy a 3 érintkezési pont egy egyenesen legyen, eszerint a pontok egy háromszög csúcsai. Legyen

k_{i}

keresett középpontja

O_{i}

(i = 1, 2, 3)

, az előbbiek szerint ezek egyike sincs rajta két érintési pont összekötő egyenesén és a 3 középpont háromszöget alkot.
Messe

k_{1}

-et a

T_{1} T_{2}

egyenes

A'

-ben,

T_{1} T_{3}

pedig

A''

-ben (2. ábra).

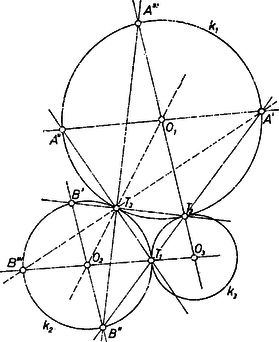2. ábra

Belátjuk, hogy

A' A''

k_{1}

-nek átmérője. Ugyanis a

T_{2} O_{1} A'

és

T_{2} O_{3} T_{1}

egyenlő szárú háromszögekben az alapok

T_{2}

közös végpontjánál levő egy-egy szög egymás csúcsszöge, ezért a két háromszög hasonló és csúcsaikat a mondott felsorolás rendjében feleltetve meg egymásnak, körüljárásuk egyező irányú. És mivel a megfelelő csúcs-párok összekötő egyenese átmegy

T_{2}

-n, azért a két háromszög centrálisan hasonló helyzetű is

T_{2}

-re mint középpontra nézve. Ezért

A' O_{1} ∥ T_{1} O_{3}

. Hasonlóan

T_{3} O_{1} A''

és

T_{3} O_{2} T_{1}

T_{3}

centrumra nézve középpontosan hasonló helyzetű háromszögek, ezért

A'' O_{1} ∥ T_{1} O_{2}

. Ámde

O_{2}

T_{1}

és

O_{3}

egy egyenes pontjai, ezért az

O_{1} A'

O_{1} A''

sugarak egymás meghosszabbításába esnek,

A' A''

k_{1}

-nek valóban átmérője, éspedig párhuzamos az

O_{2} O_{3}

egyenessel.
Ugyanígy kapjuk

k_{2}

-nek az

O_{1} O_{3}

-mal párhuzamosan haladó

B' B''

átmérőjét. És mivel

k_{1}

és

k_{2}

centrálisan hasonló helyzetűek

T_{3}

-ra mint középpontra, azért

B' B''

-nek

k_{1}

-beli megfelelője

k_{1}

-nek újabb,

A' A''

-től különböző átmérőjét adja és a két átmérő metszéspontja

O_{1}

B'

mondott megfelelője

T_{2}

B''

-ét pedig

B'' T_{3}

metszi ki ‐ legyen ez

A'''

‐, s ekkor az átmérő

T_{2} A'''

.
Összefoglalva:

O_{1}

kijelölése céljára a következő 6 egyenest rajzoltuk meg (az egyenes jele után zárójelben adjuk meg az általa meghatározott pontokat):

T_{1} T_{2} (A', B'')

T_{1} T_{3} (A'')

A' A''

T_{2} T_{3} (B')

B'' T_{3} (A''')

T_{2} A''' (O_{1})

. A további két középpont a következő 3 egyenes megrajzolásával adódik:

A' T_{3} (B''')

B' B''

B''' T_{1} (O_{2}

, valamint

O_{3}

T_{2} A'''

-ből).
Ezzel az állítást bebizonyítottuk.

Szokoli István (Miskolc, I. sz. Ipari Szakközépisk., IV. o. t.)

Hima Tamás (Budapest, Veres Pálné Gimn., I. o. t.)

Megjegyzések. 1. Az

A' A''

egyenes átmérő voltának bizonyítása nem korlátozódva a csak külső érintkezések esetére ‐ az 1950. évi Kürschák-verseny 2. feladata volt. ^{$^{*}$}
2. A fenti bizonyítás a gimnáziumi I. osztályos tananyag ismeretében is elmondható (hasonlóság és hasonló helyzet nélkül: az

A' O_{1} A''

szög egyenlő az

O_{3} O_{1} O_{2}

háromszög szögeinek összegével stb.).

Szabados György (Veszprém, Lovassy L. Gimn., I. o. t.)

^{$^{*}$}L. Hajós György‐Neukomm Gyula‐Surányi János: Matematikai versenytételek, II. rész, 2. bővített kiadás, Budapest, Tankönyvkiadó, 1965., 99. oldal.