|
| Feladat: |
F.1687 |
Korcsoport: 16-17 |
Nehézségi fok: nehéz |
| Megoldó(k): |
Angyal József , Czédli G. , Fazekas Á. , Gál P. , Gáspár Gyula , Győry Gy. , Gönczi I. , Horváthy P. , Kabay Gy. , Kérchy L. , Kuhár J. , Lakatos B. , László A. , Légrády G. , Máté Gy. , Pál J. , Prőhle T. , Sashegyi L. , Selényi P. , Szendrei Ágnes , Szendrei Mária , Tóth Béla , Turán Gy. , Vajnági A. |
| Füzet: |
1970/november,
114 - 118. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Alakzatba írt kör, Trigonometriai azonosságok, Teljes indukció módszere, Szögfüggvények, síkgeometriai számítások, Szabályos sokszögek geometriája, Alakzatok köré írt kör, Feladat |
| Hivatkozás(ok): | Feladatok: 1969/november: F.1687 |
|
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Nyilvánvalóan , így az , és a szabályos -szög oldalának fele által alkotott derékszögű háromszögből tehát (-rel végigosztva) azt kell bizonyítanunk, hogy | | (1) |
más szóval, hogy | |
Mindkét különbség pozitív, így ez az egyenlőtlenség akkor és csak akkor teljesül, ha a bal és jobb oldalának hányadosa nagyobb, mint 1. Szorzattá alakítással | | (2) |
Itt a második tényező nagyobb -nél, hiszen egyrészt | |
ezért | |
másrészt mert a sinus függvény a () nyitott intervallumban monoton növekvő és pozitív.
(2) első tényezője egyszerűbben így írható ahol | |
erről teljes indukcióval mutatjuk meg, hogy mindig nagyobb -nél, ha természetes szám.
esetén, alapján állításunk helyes. Feltéve mármost, hogy az természetes számra (3) értéke nagyobb -nél, vagyis hogy más alakban
tehát a tulajdonság valóban öröklődik (a cosinusok helyett -et írva mindkét szorzatot nagyobbal pótoltuk).
Ezek szerint (2) mindig nagyobb -nél, és ez az előrebocsátottak szerint egyértelmű a feladat állításával.
| Gáspár Gyula (Miskolc, Herman O. Gimn., II. o. t. ) |
Megjegyzés. Alsó korlátot kapunk -re, ha (1)-et felírjuk az , értékekre és a kapott egyenlőtlenségeket összeadjuk. Átrendezéssel
Jobb a becslés, ha csak az értékekre szorítkozunk
Az iskolai függvénytáblázatok 18. táblázata (58. o.) oszlopának adatai szerint -re már is áll, -re pedig is.
II. megoldás. Legyen röviden | |
Ezeket (1)-be beírva, majd -vel osztva a bizonyítandó egyenlőtlenség (csupa megfordítható átalakítással) így írható:
Ha van olyan , melyre , (, természetes számok), akkor (4) bizonyítása a következő: azt kell belátnunk, hogy Legyen az egységsugarú, középpontú kör ívéhez tartozó középponti szög , és jelöljük az pont vetületét az egyenesen -vel, a szakasz hosszát -vel . 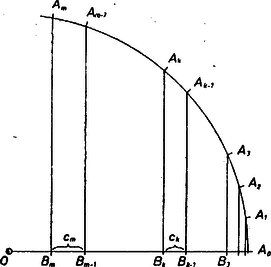 1. ábra
Mivel , , azt kell megmutatnunk, hogy (1. ábra): | |
Megmutatjuk, hogy a számok monoton nőnek: Legyen , ill. vetülete az , ill. egyenesen , ill. . Az , derékszögű háromszögek átfogója egyenlő, az elsőnek -nél levő szöge, , nagyobb, mint a másodiknak -nél levő, nagyságú szöge, tehát e szögekkel szemközti befogók közül az elsőé a nagyobb, , vagyis (2. ábra). 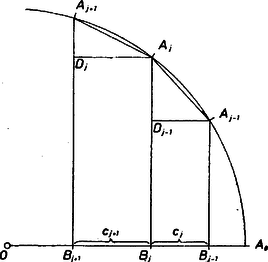 2. ábra
Legyen most ekkor elegendő megmutatnunk, hogy :
ami valóban igaz, hiszen a bal oldali összeg minden tagja kisebb -nél. Ezzel bebizonyítottuk (4)-et minden olyan esetre, amikor racionális. Ez pedig feladatunkban fennáll, mert .
Megjegyzések. 1. Szemléletes értelmezését adjuk (4)-nek. A két oldalon a függvényt ábrázoló görbe két húrjának iránytangense áll, éspedig a (, ), ill. (, ) intervallum fölötti , ill. görbeív végpontjait összekötő húré (3. ábra). 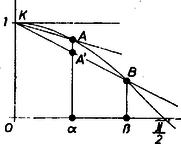 3. ábra
Fogadjuk el a szemlélet alapján (azaz bizonyítás nélkül), hogy grafikonja a () intervallumban konkáv (alulról, vagyis az tengely pozitív irányába nézve), ami azt jelenti, hogy bármely részívének végpontjait összekötve, az ív a kapott húr fölött halad. Eszerint, az pontbeli ordinátaegyenes és metszéspontját -vel jelölve, , így a egyenes meredekebben süllyed, mint , tehát (4) bal oldala valóban nagyobb (kisebb abszolút értékű negatív szám), mint a jobb oldala.
| Angyal József (Budapest, Berzsenyi D. Gimn., III. o. t.) |
2. Az elfogadott állítást némileg alátámasztja, hogy bármely , -re, hacsak a grafikonján az intervallum fölötti ív végpontjait összekötő húr felezőpontja alatta van az ívnek. Ennek koordinátái ugyanis és | |
mert mindkét tényező pozitív, hiszen
3. Más alátámasztása a konkávságnak: deriváltja, érintőjének iránytangense , és ez a mondott intervallumban monoton csökken, a görbe lefelé ,,kanyarodik'' (a második derivált: ).
Hack F.: Függvénytáblázatok, matematikai összefüggések. Tankönyvkiadó, Budapest, 1969. |
|
 PDF |
PDF |  MathML
MathML 

