Kezdőlap


Feladat:	F.1686	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Balogh Z. , Bartholy Judit , Bognár B. , Boros E. , Bruckner Lívia , Fazekas Á. , Fazekas G. , Feind F. , Fejes G. (IV. o. Bpest) , Ferró J. , Frankl P. , Füredi Z. , Gál P. , Garay B. , Gáspár Gy. , Golda J. , Göndőcs F. , Hadik R. , Hangos Katalin , Hermann T. , Horváthy Péter , Juhász Júlia , Kacsuk P. , Kérchy L. , Kiss Ipoly , Komornik V. , Kökényesi Gy. , Lakatos B. , Maróti Gy. , Pál J. , Pap Gy. , Poór Zs. , Prőhle T. , Reviczky J. , Sailer K. , Selényi P. , Skopál I. , Szepesi L. , Vajnági A. , Zárboch Zs.
Füzet:	1970/november, 113 - 114. oldal		PDF \| MathML
Témakör(ök):	Pont körüli forgatás, Szögfelező egyenes, Koszinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1969/november: F.1686

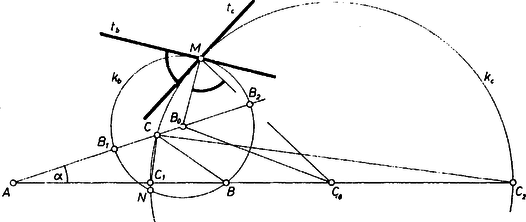
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Válasszuk úgy az $A B C$ háromszög betűzését, hogy a szokásos jelölésekkel $a < b < c$ teljesüljön. Az állítást a $C$ és $B$ csúcsokból kiindulva kapott körökre bizonyítjuk, ennek mintájára végezhető a bizonyítás a további két körpár esetére is.

Legyen a

C

-ből induló belső és külső szögfelezőnek az

A B

egyenessel való metszéspontja

C_{1}

, ill.

C_{2}

, a

C_{1} C_{2}

szakasz fölötti

k_{c}

Thalész-kör középpontja

C_{0}

, a

B

-ből kiindulva ugyanígy kapott pontok és kör rendre

B_{1}

B_{2}

B_{0}

k_{b}

, végül

k_{b}

és

k_{c}

egyik metszéspontja

M

. A körök

M

-beli

t_{c}

t_{b}

érintőjét

M

körül

90^{\circ}

-kal elfordítva a megfelelő sugarak

M C_{0}

M B_{0}

egyenesét kapjuk, így elegendő azt belátni, hogy a

B_{0} M C_{0} ∢

értéke

60^{\circ}

vagy

120^{\circ}

, azaz hogy

\begin{matrix} | cos B_{0} M C_{0} ∢ | = \frac{| M B_{0}^{2} + M C_{0}^{2} + B_{0} C_{0}^{2} |}{2 M B_{0} \cdot M C_{0}} = \frac{1}{2} \end{matrix}

(1)

a < b

miatt

C_{1}

C_{2}

A

-nak ugyanazon oldalán vannak, mint

B

és így

C_{0}

is ezen az oldalon van, ennélfogva a szögfelezők osztásarányának tétele alapján

\begin{matrix} A C_{0} = \frac{A C_{1}}{2} + \frac{A C_{2}}{2} = \frac{b c}{2 (b + a)} + \frac{b c}{2 (b - a)} = \frac{b^{2} c}{b^{2} - a^{2}}, \end{matrix}

és ugyanezekkel a szakaszokkal

\begin{matrix} M C_{0} = C_{1} C_{0} = \frac{A C_{2} - A C_{1}}{2} = \frac{a b c}{b^{2} - a^{2}}; \end{matrix}

továbbá hasonlóan

\begin{matrix} A B_{0} = \frac{c^{2} b}{c^{2} - a^{2}}, M B_{0} = B_{1} B_{0} = \frac{a b c}{c^{2} - a^{2}} . \end{matrix}

Ezekkel az (1)-beli számláló, a cosinustételt az

A B_{0} C_{0}

háromszögre és az

A B C

háromszögre alkalmazva:

\begin{matrix} | (M B_{0}^{2} - A B_{0}^{2}) + (M C_{0}^{2} - A C_{0}^{2}) + 2 A B_{0} \cdot A C_{0} cos α | = \\ = | - \frac{b^{2} c^{2}}{c^{2} - a^{2}} - \frac{b^{2} c^{2}}{b^{2} - a^{2}} + \frac{b^{2} c^{2} (b^{2} + c^{2} - a^{2})}{(b^{2} - a^{2}) (c^{2} - a^{2})} | = \frac{a^{2} b^{2} c^{2}}{(b^{2} - a^{2}) (c^{2} - a^{2})} = M B_{0} \cdot M C_{0}, \end{matrix}

tehát (1) valóban fennáll. Ezt akartuk bizonyítani.

Horváthy Péter (Budapest, Fazekas M. Gyak. Gimn., IV. o.t.)