Kezdőlap


Feladat:	F.1683	Korcsoport: 14-15	Nehézségi fok: nehéz
Megoldó(k):	Bálint László , Fejes Gábor , Garay Barnabás , Hollósy Gábor , Molnár József , Török István
Füzet:	1970/szeptember, 14 - 17. oldal		PDF \| MathML
Témakör(ök):	Algebrai átalakítások, Paraméteres egyenlőtlenségek, Egységtörtes felbontás, Teljes indukció módszere, Feladat
Hivatkozás(ok):	Feladatok: 1969/november: F.1683

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. I. Az első állítást a teljes indukció módszerével bizonyítjuk, az (1) bal oldalán álló kifejezést $s_{n}$ -nel jelöljük. $n = 1$ esetén $s_{1} = 1 / 2 + 1 / 3 + 1 / 4 = 13 / 12 > 1$ , az állítás igaz. Ha mármost $k$ olyan természetes szám, amelyre $s_{k} - 1 > 0$ , akkor $k + 1$ esetében

\begin{matrix} s_{k + 1} - 1 = (s_{k} - 1) & - \frac{1}{k + 1} + \frac{1}{3 k + 2} + \frac{1}{3 (k + 1)} + \frac{1}{3 k + 4} = \\ = (s_{k} - 1) & + \frac{1}{3 k + 2} - \frac{2}{3 (k + 1)} + \frac{1}{3 k + 4} = \\ = (s_{k} - 1) & + (\frac{1}{3 k + 2} - \frac{1}{3 k + 3}) - (\frac{1}{3 k + 3} - \frac{1}{3 k + 4}) = \\ = (s_{k} - 1) & + \frac{1}{(3 k + 2) (3 k + 3)} - \frac{1}{(3 k + 3) (3 k + 4)} = \\ = (s_{k} - 1) & + \frac{1}{3 k + 3} (\frac{1}{3 k + 2} - \frac{1}{3 k + 4}) > s_{k} - 1 > 0, \end{matrix}

mert az elhagyott tag pozitív, vagyis az állítás igaz volta átöröklődik

k

-ról

k + 1

-re. Ezzel (1)-et igazoltuk.
II. Úgy választjuk meg

r

-et a

\begin{matrix} H_{r} = 1 + \frac{1}{2} + \frac{1}{3} + ... + \frac{1}{r} \end{matrix}

összegben, hogy

H_{r}

egy adott

A

számnál nagyobb legyen. Ez negatív

A

esetén

r = 1

-re is teljesül. Ha

A \geq 0

, feltehetjük, hogy pozitív egész, mert ha nem az, felkerekítjük a következő pozitív egésszé. Ezután

H_{r}

-nek

1

utáni részét

A - 1

olyan részösszegből állítjuk össze, amilyen (1) bal oldalán áll, az elsőben

n

-et

1

-nek választva. Az így fellépő utolsó tört nevezőjét választjuk

r

-nek. Ezzel a feladat második állítását lényegében már bebizonyítottuk.
Szemléletesebbé tesszük bizonyításunkat, közelebbről meghatározva az

A

(pozitív egész) számhoz tartozó

r

-et.

H_{r}

mondott

k

-adik szeletében (elsőnek az

1 = 1 / 1

-et tekintjük) az utolsó tag nevezőjét

a_{k}

-val jelölve, ez

1

-gyel nagyobb, mint az előző szeletbeli megfelelőjének,

a_{k - 1}

-nek

3

-szorosa, ennélfogva a szelet utolsó tagjának nevezője

\begin{matrix} a_{1} = 1, a_{k} = 3 a_{k - 1} + 1 (k = 2,3, ...) . \end{matrix}

(2)

Eszerint

\begin{matrix} a_{2} = 3 + 1 = \frac{3^{2} - 1}{3 - 1} = 4, a_{3} = (3^{2} + 3) + 1 = \frac{3^{3} - 1}{2} = 13, \end{matrix}

és a látható

a_{k} = (3^{k} - 1) / 2

szabályszerűséget általában igazolja (2), így az

A

sorszámú szelet utolsó tagjának nevezője

\begin{matrix} a_{A} = \frac{3^{A} - 1}{2} = r . \end{matrix}

(3)

Eddig a határig véve a természetes számok reciprokát, összegük nagyobb

A

-nál.
Természetesen hasonlóan akkor is kijelölhetnénk elegendő számú természetes számot, ha mondjuk csak az

1000

-nél nagyobbak közül választhatnánk.
III. Az előírt

A = 4, 5

-et

5

-re kerekítve (3) szerint

r = 121

. Ha viszont észrevesszük, hogy

A - H_{2} = 3

, egész szám, akkor (1)-et

3

-szor alkalmazva a (2) rekurzív képlet alapján

n = 2

-re,

7

-re és

22

-re, ezt írhatjuk:

\begin{matrix} (1 + \frac{1}{2}) + (\frac{1}{3} + \frac{1}{4} + ... + \frac{1}{7}) + (\frac{1}{8} + ... + \frac{1}{22}) + (\frac{1}{23} + ... + \frac{1}{67}) = H_{67} > 4,5. \end{matrix}

Bálint László (Budapest, Móricz Zs. Gimn., II. o. t.)

A továbbiakban csak az (1) állításra adunk más bizonyításokat.

II. megoldás. (1) bal oldala elölről és hátulról számított

k

-adik tagjának összege

(k = 1,2, ..., n)

\begin{matrix} \frac{1}{n + k} + \frac{1}{3 n + 2 - k} = \frac{4 n + 2}{{2 n + 1 - (n + 1 - k)} \cdot {2 n + 1 + (n + 1 - k)}} = \\ = \frac{4 n + 2}{{(2 n + 1)}^{2} - {(n + 1 - k)}^{2}} > \frac{2 (2 n + 1)}{{(2 n + 1)}^{2}} = \frac{2}{2 n + 1} . & (5) \end{matrix}

Ilyen pár

n

van, a középső

1 / (2 n + 1)

-nek nem jut pár. Így pedig

\begin{matrix} s_{n} > n \cdot \frac{2}{2 n + 1} + \frac{1}{2 n + 1} = 1, \end{matrix}

amit bizonyítanunk kellett.

Török István (Esztergom, Hell J. Bányagép. Techn., IV. o. t.)

Molnár József (Baja, III. Béla Gimn., II. o. t.)

Megjegyzések. 1. A meggondolás szemléletes megfelelője a következő: az

y = 1 / x

görbének az

x > 0

tartomány fölötti íve (alulról, vagyis a pozitív

y

tengely irányába nézve) konvex, bármely részívének minden belső pontja alatta van a részív végpontjait összekötő húrnak.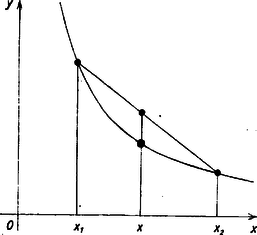

1. ábra

Valóban, az

(x_{1}, \frac{1}{x_{1}})

(x_{2}, \frac{1}{x_{2}})

pontokat összekötő szelő egyenlete (1. ábra):

\begin{matrix} y_{h} = \frac{1}{x_{1}} + \frac{\frac{1}{x_{2}} - \frac{1}{x_{1}}}{x_{2} - x_{1}} (x - x_{1}) = \frac{1}{x_{1}} - \frac{x - x_{1}}{x_{1} x_{2}}, \end{matrix}

és így a húr és a görbe ordinátáinak különbsége az

x_{1}

és

x_{2}

abszcisszák közti

x

pontban, vagyis ha

0 < x_{1} < x < x_{2}

\begin{matrix} y_{h} - \frac{1}{x} = (\frac{1}{x_{1}} - \frac{1}{x}) - \frac{x - x_{1}}{x_{1} x_{2}} = \frac{(x - x_{1}) (x_{2} - x)}{x x_{1} x_{2}} > 0. \end{matrix}

Ezt fent az

\begin{matrix} x_{1} = n + k, x_{2} = 3 n + 2 - k, x = \frac{x_{1} + x_{2}}{2} = 2 n + 1 \end{matrix}

értékhármas esetében láttuk, (5) ‐ ha

2

-vel osztjuk ‐ azt fejezi ki, hogy az

x

-tengely és az

1 / x

görbe

x_{1}

és

x_{2}

abszcisszájú pontjaival meghatározott trapéz középvonala nagyobb, mint a görbének a középvonalon levő pontjához tartozó ordináta.

Hollósy Gábor és Garay Barnabás (Sopron, Széchenyi I. Gimn., III. o. t.)

2. Hasonló a következő bizonyítás. Egy félkörív

4 n + 2

egységnyi átmérőjét egységnyi szakaszokra osztva, az

n + k

és

3 n + 2 - k

részekre osztó pontban emelt merőlegesnek a körív alatti szakasza

k = 1,2, ..., n

esetén kisebb a középpontban emelt merőleges megfelelő szakaszánál, ami pedig

2 n + 1

; így a szakaszok négyzetére, ismert tétel szerint (2. ábra):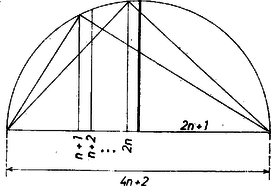

2. ábra

\begin{matrix} (n + k) (3 n + 2 - k) < {(2 n + 1)}^{2} . \end{matrix}

Reciprokukat véve és

4 n + 2

-vel szorozva ismét (5)-re jutunk:

\begin{matrix} \frac{(3 n + 2 - k) + (n + k)}{(n + k) (3 n + 2 - k)} = \frac{1}{n + k} + \frac{1}{3 n + 2 - k} > \frac{2}{2 n + 1} . \end{matrix}

Fejes Gábor (Budapest, Kossuth L. Gimn., IV. o. t.)