Kezdőlap


Feladat:	F.1681	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	B. Nagy Péter , Baintner László , Berényi P. , Boros E. , Cserháti A. , Fazekas Á. , Feind F. , Frankl P. , Füredi Z. , Földes T. , Gál P. , Garay B. , Gáspár Gy. , Glódy A. , Győry Gy. , Görbe M. , Hangos Katalin , Hermann T. , Hetzer J. , Hoffer J. , Horváth Miklós , Horváthy P. , Kelen M. , Kisvarga J. , Komornik V. , Lévai G. , Major Imre , Maróti Gy. , Mártonfi Gy. , Máté Gy. , Monostori L. , Morvai I. , Nagy Ferenc , Nagy Károly , Nagy Sándor (Bp. I. István) , Nyilánszky M. , Pásztor I. , Pataki B. , Pattantyús P. , Poór Zs. , Prácser E. , Rudas T. , Sebő A. , Selényi P. , Simon Júlia , Simonyi Gy. , Stiebel J. , Szendrei Ágnes , Szendrei Mária , Szepesi L. , Szigeti M. , Tegze M. , Tóth Béla , Turán Gy. , Vajnági A. , Várgedő T. , Zoltán L.
Füzet:	1970/május, 207 - 211. oldal		PDF \| MathML
Témakör(ök):	Tengely körüli forgatás, Középpontos és egyéb hasonlósági transzformációk, Vetítések, Szerkesztések a térben, Gömb és részei, Szabályos tetraéder, Feladat
Hivatkozás(ok):	Feladatok: 1969/október: F.1681

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. I. Legyenek az előírt negyedelő pontok rendre $A_{0}$ , $B_{0}$ , $C_{0}$ (azaz pl. $D C_{0} = 3 D C / 4$ ). Ezek nincsenek egy egyenesen, mert az $A_{0} B_{0}$ egyenes benne van a $D A B$ síkban, $C_{0}$ pedig nincs benne (1. ábra), így ez a $3$ pont egy síkot határoz meg, jelöljük ezt 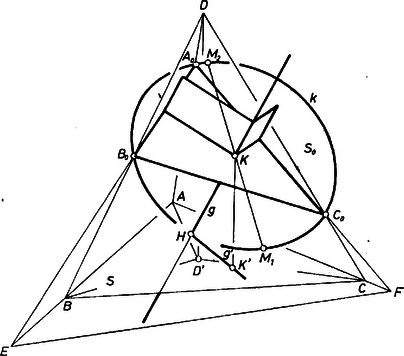$S_{0}$ lal.

1. ábra

Legyen az

A_{0} B_{0} C_{0}

háromszög köré írt

k

kör középpontja

K

, ekkor a háromszög csúcsaitól egyenlő távolságban levő pontok mértani helye a

K

-ban

S

,-ra állított

g

merőleges, ezért a keresett

G

gömb

O

középpontja

g

-n lesz,

G

-nek az

S

-en való

O'

érintési pontja pedig

g

-nek az

A B C = S

alapsíkon levő

g'

vetületén lesz. Amennyiben

G

létezik, a

k

kör mindenesetre rajta van

G

-n. (

g

nem merőleges

S

-re ‐ csak akkor lenne merőleges, ha

S_{0}

párhuzamos lenne

S

-sel, ez azonban nem áll, hiszen pl.

A_{0}

és

B_{0}

más-más távolságban van

S

-től ‐, ezért

g'

nem pont.)

g'

-t meghatározza

g

-nek (

S

-en való)

H

döféspontja és

K

-nak

K'

vetülete. (

H

létrejön, mert

g

nem párhuzamos

S

-sel; akkor lenne párhuzamos vele, ha

S_{0}

merőleges lenne

S

-re, vagyis ha

A_{0}

B_{0}

C_{0}

-nak

S

-en levő vetülete egy egyenesbe esnék, ez viszont nem áll fenn, mert e három vetület az

A B C

szabályos háromszög köré írt körnek rendre a

D' A

D' B

D' C

sugarán van ‐ ahol

D'

D

csúcs vetülete ‐ és annak rendre első, második, harmadik negyedelő pontja.)
Mindazok a gömbök, amelyek

g'

valamely pontjában érintik

S

-et és középpontjuk a

g

-n van, páronként egymás képei abban a

H

centrumú középpontos hasonlóságban, melynek aránymutatója egyenlő sugaraik arányával. A

g'

-n átmenő minden egyes sík (

S

-et kivéve)

G

-ből ‐ és bármely az imént mondott gömbből is ‐ kört metsz ki, és ez érinti

g'

-t, középpontja

O

-nak ‐ ill. a gömb középpontjának ‐ a metsző síkon levő vetülete. Válasszunk tetszés szerint egy ilyen

S_{t}

síkot és egyet a mondott gömbök közül, legyen ez (a

G

-től különböző)

G^{*}

. Ekkor a

G

-ből és

G^{*}

-bó1

S_{t}

által kimetszett

k_{t}

k_{t}^{*}

körök is egymás képei a

H

centrumú,

R : R^{*}

aránymutatójú (

R

R^{*}

a gömbök sugarai) középpontos hasonlóságban,

K_{t}

K_{t}^{*}

középpontjuk

g

-nek

S_{t}

-n levő

g_{t}

vetületén van (amely természetesen átmegy

H

-n, 2. ábra).

2. ábra

Ezek alapján a következő lépésekben kapjuk

G

-t.

S_{t}

-nek (pl.) az előírt

C_{0}

-on átmenő síkot választjuk,

g_{t}

-nek egy tetszés szerinti

K_{t}^{*}

pontja körül a

g'

-t érintő

k_{t}^{*}

kört írunk, ezt metsszük a

H C_{0}

egyenessel a

C_{0}^{* 1}

C_{0}^{* 2}

pontokban; (feltéve, hogy ezek létrejöttek)

C_{0}

-on át párhuzamost húzunk

C_{0}^{* 1} K_{t}^{*}

-gal és

C_{0}^{* 2} K_{t}^{*}

-gal, ekkor a

g_{t}

-n kapott

K_{t 1}

K_{t 2}

metszésponton át

S_{t}

-re (más szóval a

g

g_{t}

síkban

g_{t}

-re) állított merőleges

g

-ből kimetszi a keresett

G_{1}

G_{2}

gömb

O_{1}

, ill.

O_{2}

középpontját, a gömb sugara pedig természetesen ennek

S

-től (más szóval

g'

-től) mért

O_{1} O_{1}'

, ill.

O_{2} O_{2}'

távolsága (3. ábra).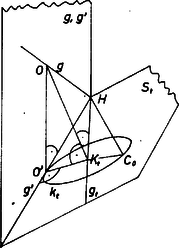

3. ábra

II. A feladathoz fűzött megjegyzés értelmében

g

A_{0} B_{0}

és

A_{0} C_{0}

szakaszok felező merőleges síkjának metszésvonala. Egy-egy ilyen síkot a szakasz két felező merőleges egyenese határoz meg, pl.

A_{0} B_{0}

-é egyrészt

S_{0}

-ban, másrészt egy az

A_{0} B_{0}

-on átmenő,

C_{0}

-t nem tartalmazó síkban. (A sík két metsző egyenese egyenértékű a sík

3

, nem egy egyenesen levő pontjával.)
Hasonlóan kaphatjuk a

g

-re

H

-ban emelt merőleges síkot (

g

-n egy

H

közepű szakaszt kijelölve), ennek

S

-sel való metszésvonalára

H

-n át (

S

-ben) állított merőleges megadja

g'

-t. A többi mondott szerkesztést egy-egy síkban végeztük. (Síkbeli szerkesztéseknél nem szoktunk különbséget tenni a megengedett lépések elvi felhasználása, és azok körzővel ‐ vonalzóval való végrehajtása között. Térbeli szerkesztéseknél azonban ‐ mivel a megfelelő eszközök hiányoznak ‐ a szerkesztés leírása csak a megengedett lépések alkalmas sorrendjét adja meg, és nem szolgál valamilyen szerkesztési eljárás vázlatául.)
III. Eredményünk helyes voltának bizonyításában csak azt kell belátnunk, hogy

G_{i} (i = 1, 2)

átmegy

C_{0}

-on, hiszen akkor átmegy

A_{0}

-on,

B_{0}

-on is. Ehhez megjegyezzük, hogy

K_{t i}

-nek

g'

-n levő vetülete éppen

O_{i}'

. Ugyanis

g'

-re

O_{i} O_{i}'

is,

O_{i} K_{t i}

is merőlegesen áll ‐ utóbbi azért, mert merőleges a

g'

-t tartalmazó

S_{t}

-re ‐, így az

O_{i} O_{i}' K_{t i}

sík s vele az

O_{i}' K_{t i}

egyenes merőleges

g'

-re.
Legyen

K_{t}^{*}

-nak

g'

-n levő vetülete, azaz

k_{t}^{*}

és

g'

érintkezési pontja

K_{t}^{*}'

ekkor szerkesztésünk szerint

C_{0} K_{t i} O_{i}'

a háromszög a

C_{0}^{* i} K_{t}^{*} K_{t}^{*}'

háromszög képe a

H

centrumú,

H C_{0} : H C_{0}^{* i}

arányú középpontos hasonlóságban. Így

C_{0}^{* i} K_{t}^{*} = K_{t}^{*}' K_{t}^{*}

alapján

C_{0} K_{t i} = O_{i}' K_{t i}

, vagyis

C_{0}

rajta van a

K_{t i}

középpontú,

K_{t i} O_{i}'

sugarú körön, ami pedig

G_{i}

-nek

S_{t}

-vel való metszésvonala. Ezt akartuk bizonyítani.
IV.

G_{i}

létezése és a megoldások száma azon múlik, hány közös pontja van a

H C_{0}

egyenesnek

k_{t}^{*}

-vel. Amennyiben az

A_{0} B_{0} C_{0}

háromszög köré írt

k

körnek volna pontja az

S

-sel kettévágott tér

D

-t nem tartalmazó felében, akkor a feladatnak nem volna megoldása. Esetünkben ‐ mint a II. megoldásban majd látjuk ‐ feladatunknak két gömb tesz eleget.

Baintner László (Budaoest, Teleki Blanak Gimn., IV. o. t. )

dolgozata alapján, egyszerűsítésekkel és kiegészítésekkel

Megjegyzés. Egyszerűbb, de az eredeti adatok felhasználásától jobban eltávolodó meggondolás a következő. Keressük meg a fenti

k

-nak

M_{1}

M_{2}

metszéspontjait a

g

g'

síkon. Ekkor a

g'

-t érintő és

M_{1}

-en,

M_{2}

-n átmenő kör, ami hasonlósági transzformációval ismert módon megszerkeszthető, hacsak

M_{1}

M_{2}

mindegyike

g'

-nek ugyanazon oldalán van,

G

-nek egy főkörét adja meg. A mondott két pontot úgy kapjuk, hogy a mondott síkban

K

-n át merőlegest állítunk

g

-re és erre mindkét irányban felmérjük

k

-nak

K A_{0}

sugarát (4. ábra).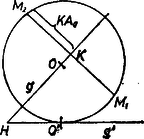

4. ábra

II. megoldás. Könnyű megszerkeszteni az

O

gömbközéppontnak az

S

alapsíkon levő

O'

vetületét, a gömb érintési pontját. A fenti jelöléseket tovább használva messe

A_{0} B_{0}

A B

egyenest

E

-ben,

A_{0} C_{0}

A C

-t

F

-ben. Ekkor

E O'

érintője,

E A_{0}

pedig szelője annak a körnek, amelyet a

G

-ből az

A_{0} B_{0} O'

sík metsz ki, ezért

E O'

hossza egyenlő az

E A_{0}

E B_{0}

szakaszok mértani középarányosával. Hasonlóan

F O' = \sqrt[]{F A_{0} \cdot F C_{0}}

, és így

E

F

körül

E O'

, ill.

F O'

sugarú kört írva, közös pontjuk

O'

.
Ezután

O

-t az

O' A_{0}

szakasz felező merőleges síkja metszi ki az

S

-re

O'

-ben állított merőleges egyenesből. (Ezzel megkapjuk a gömb

O O'

sugarát.)
Ügyes egyszerűsítésekkel a szerkesztés

S

-beli részét egyetlen ábrán belül végrehajthatjuk, a külső pontoknak

S

-en levő vetületét a pont jele mellé tett vesszővel jelöljük (5. ábra).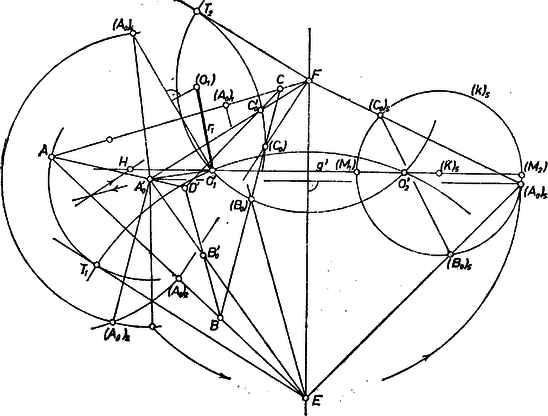

5. ábra

E

-t nyilvánvalóan megadja

A B

és

A_{0}' B_{0}'

közös pontja, de megkapjuk úgy is, hogy az

A B D

háromszöget

A B

körül úgy fordítjuk bele

S

-be, hogy

D

C

-be jusson. Ekkor

A_{0}

-nak,

B_{0}

-nak

{(A_{0})}_{1}

(B_{0})

új helyzete

C A

-nak első, ill.

C B

-nek második negyedelő pontja, és

E

-t kimetszi az

{(A_{0})}_{1} (B_{0})

egyenes. Azért célszerűbb ez, mert így az

E A_{0}

E B_{0}

szakasz

E {(A_{0})}_{1}

-ben,

E (B_{0})

-ban mindjárt valódi nagyságban látszik. Mértani közepüket úgy szerkesztettük, hogy vettük az

E T_{1}

érintőt az

A_{0}'

közepű,

A

-n átmenő körhöz. (Az olvasóra hagyjuk annak belátását, hogy ez a kör átmegy

{(A_{0})}_{1}

és

(B_{0})

mindegyikén.)
Hasonlóan, az

A C D

háromszöget az

A C B

helyzetbe lefordítva az

A_{0} C_{0}

egyenes új,

{(A_{0})}_{2} (C_{0})

helyzete kimetszi

A C

-ből

F

-et, és az így valódi nagyságban látszó

F A_{0}

F C_{0}

szakaszok mértani középarányosa az az

F T_{2}

érintő szakasz, amit az

A C

szakasz első negyedelőpontja körüli,

(C_{0})

-on átmenő körhöz húztunk

F

-ből. A fent mondott két kör közös pontjai

O_{1}'

O_{2}'

. (Létezésük mutatja, hogy

2

megoldás van; megjegyezzük csupán, hogy ha a fenti

k

kör túlnyúlna az

S

síkon, akkor a két körnek nem lenne közös pontja.)
Megszerkesztettük ábránkon az

O_{1}'

-ben érintő

G_{1}

gömb sugarát is, az

O_{1}' O_{1} A_{0}

síknak

O_{1}' A_{0}'

körül a rajz síkjába való belefordításával. Ehhez

A_{0}

-nak

S

fölötti

A_{0}' A_{0}

magasságát az

A A_{0} A_{0}'

háromszögnek

S

-be, az

A {(A_{0})}_{3} A_{0}'

helyzetbe fordításával kaptuk,

{(A_{0})}_{3}

A_{0}'

-ben

A_{0}' A

-ra állított merő1eges és az

A

körüli,

A A_{0} = A {(A_{0})}_{2}

sugarú kör metszéspontja. Ezt

A_{0}'

körül ráfordítva az

A_{0}'

-ben

O_{1}' A_{0}'

-re állított merőlegesre, kaptuk

A_{0}

-nak az

O_{1}' A_{0}'

tengely körül

S

-be fordított

{(A_{0})}_{4}

helyzetét, végül az

{(A_{0})}_{4} O_{1}'

szakasz felező merőlegesével az

O_{1}'

-ben

O_{1}' A_{0}'

-re állitott merőlegesből kimetszettük

O_{1}

-nek

S

-be átfordított

(O_{1})

képét. Így

G_{1}

, sugara

O_{1}' (O_{1})

Megjegyzések. 1. Az

E F

egyenes

S

és

S_{0}

metszésvonala, e körül az

A_{0} B_{0} C_{0}

háromszöget

S

-be fordítva megkapjuk valódi nagyságát:

{(A_{0})}_{5} {(B_{0})}_{5} {(C_{0})}_{5}

(A_{0})

-nak

E F

-től való távolsága annak a derékszögű háromszögnek az átfogója, melynek egyik befogója

A_{0}

-nak fent megszerkesztett magassága, másik befogója pedig

A_{0}'

-nek

E F

-től való távolsága. (

K

-nak

{(K)}_{5}

befordított helyzete természetesen az

O_{1}' O_{2}'

egyenesen van, ami az I. megoldásbeli

g'

egyenes. Szemlélet szerint

C_{0} A_{0} = C_{0} B_{0}

, de ez enélkül is könnyen belátható. Ez megkönnyíti

k

sugarának kiszámítását. Néhány, az I. megoldás szerint haladó dolgozat, erre támaszkodva mutatta meg, hogy

k

nem nyúlik át

S

túlsó oldalára.
2. Az I. megoldásbeli

H

pontot is könnyű megszerkeszteni két olyan egyenes metszéspontjaként, amelyet a

g

-t meghatározó felező merőleges síkok metszenek ki

S

-ből. Pl.

A_{0} B_{0}

felező merőleges síkja

S

-et abban az egyenesben metszi, amelynek egy pontja a szakasz

A B D

síkbeli felező merőlegesének

A B

-n levő pontja (amit a fentiek szerint

{(A_{0})}_{1} (B_{0})

felező merőlegese is kimetsz), és amely továbbá merőleges

A_{0}' B_{0}'

-re.

H

természetesen szintén az

O_{1}' O_{2}'

egyenesen adódik.