Kezdőlap


Feladat:	F.1679	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Vas Zoltán
Füzet:	1970/április, 151 - 152. oldal		PDF \| MathML
Témakör(ök):	Egyenletek grafikus megoldása, Paraméteres egyenletek, Egészrész, törtrész függvények, Feladat
Hivatkozás(ok):	Feladatok: 1969/október: F.1679

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Grafikusan úgy kapjuk az adott egyenletek megoldását, hogy bal oldalukat ábrázoljuk és ezt metsszük a (jobb oldalt ábrázoló) $y = c$ egyenessel.
A bal oldal $[x / 2]$ tagja ún. lépcsős függvény, 2 egységnyi szakaszonként állandó, a páros $x$ értékeknél szakadása van, 1 egységet ugrik. Egyenleteink bal oldalának grafikonját úgy kapjuk tehát, hogy az $y = x$ egyenest minden $2 k$ egész abszcissza értéknél megszakítjuk és a $2 k, 2 k + 2$ abszcisszák közti szakaszt ‐ a bal végpontját hozzáértve, a jobb végpontját nem ‐ eltoljuk $k$ egységgel az $y$ tengely irányában.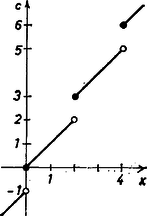

1. ábra

Így az a) egyenlet bal oldalának képén az

x

tengely balról zárt

[2 k, 2 k + 2)

intervalluma fölötti szakasz pontjainak ordinátáira

3 k \leq x + [\frac{x}{2}] < 3 k + 2

, a következő

[2 k + 2, 2 k + 4)

szakasz ordinátáira

3 k + 3 \leq x + [\frac{x}{2}] < 3 k + 5

, ezért a

3 k + 2 \leq y < 3 k + 3

értékek nem tartoznak bele az értékkészletbe. Ha

c

ilyen érték, vagyis ha

\begin{matrix} [c - 3 [\frac{c}{3}]] = 2, \end{matrix}

akkor a)-nak nincs megoldása, különben 1 megoldása van. Éspedig ha

3 k \leq c < 3 k + 2

, akkor ‐ mivel a grafikonszakasz pontjainak abszcisszája

k

-val kisebb, az ordinátájuknál ‐, a metszéspontra

\begin{matrix} x = c - k = c - [\frac{c}{3}] . \end{matrix}

(Érvényességi feltétele más alakban: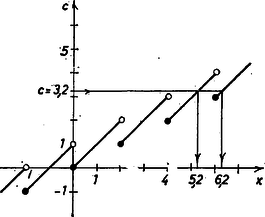

\begin{matrix} [c - 3 [\frac{c}{3}]] = 0, vagy 1.) \end{matrix}

2. ábra

A b) egyenlet esetében hasonlóan

\begin{matrix} ha 2 k \leq x < 2 k + 2, & akkor & k \leq x - [\frac{x}{2}] < k + 2, & (1) \\ és ha 2 k + 2 \leq x < 2 k + 4, & akkor & k + 1 \leq x - [\frac{x}{2}] < k + 3, & (2) \end{matrix}

vagyis a bal oldal a

\begin{matrix} k + 1 \leq c < k + 2 \end{matrix}

(3)

értékeket mindkét intervallumban felveszi. Eszerint minden valós értéket pontosan 2-szer vesz fel, az egyenletnek bármely

c

esetén két megoldása van. A grafikon és az

y = c

egyenes metszéspontjának abszcisszája az (1) intervallumban

k

-val, (2)-ben pedig

k + 1

-gyel nagyobb, mint az ordinátája, továbbá (3) szerint

k = [c] - 1

, ezért a megoldás:

\begin{matrix} x_{1} = c + [c] - 1, ill. x_{2} = c + [c] . \end{matrix}

Vas Zoltán (Szeged, Radnóti M. Gimn., III. o. t.)