Kezdőlap


Feladat:	F.1674	Korcsoport: 14-15	Nehézségi fok: átlagos
Füzet:	1970/február, 53 - 54. oldal		PDF \| MathML
Témakör(ök):	Középpontos tükrözés, Körülírt kör, Súlypont, Magasságpont, Diszkusszió, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1969/szeptember: F.1674

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a keresett $A B C$ háromszög körülírt köre $k$ , súlypontja $S$ , magasságpontja $M$ , $k$ középpontja $O$ . Az $A O = r$ , $A S = s_{0}$ , $A M = m_{0}$ szakaszokból kell megszerkeszteni a háromszöget.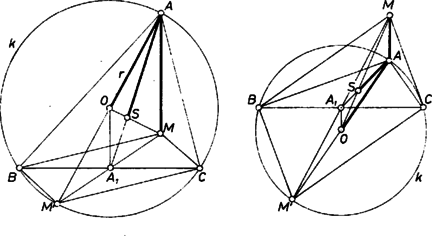
Jelöljük a $B C$ oldal felezőpontját $A_{1}$ -gyel, $M$ tükörképét $A_{1}$ -re $M'$ -vel. Ekkor $B M'$ , $C M'$ a $C M$ , ill. $B M$ tükörképe, s így merőleges $A B$ -re, ill. $A C$ -re. Eszerint $B$ és $C$ az $A M'$ szakasz fölötti Thalész-körön van. Ez a kör tehát azonos $k$ -val. Így azt nyertük, hogy a magasságpontnak a $B C$ oldal felezőpontjára vonatkozó $M'$ tükörképe a háromszög köré írt körön van, annak az $A$ csúccsal átellenes pontja. Eszerint az $A M M'$ háromszögben $A_{1}$ és $O$ oldalfelező pontok. Így $A_{1} O = A M / 2 = m_{0} / 2$ .
Az elemzés a következő szerkesztésre vezet: az $A A_{1} = s_{a} = 3 s_{0} / 2$ , $A_{1} O = m_{0} / 2$ , $O A = r$ távolságokból háromszöget szerkesztünk, $O$ körül $A$ -n át $k$ kört húzunk. Ebből metszi ki az $O A_{1}$ -re $A_{1}$ -ben állított merőleges $B$ -t és $C$ -t.

Ha a háromszög létrejön, egyértelműen meg van határozva és megfelel a feltételeknek. Jelöljük ugyanis

k

-nak

A

-val átellenes pontját

M'

-vel,

M'

tükörképét

A_{1}

-re

M

-mel. Ekkor

A M ∥ O A_{1} ⊥ B C

A M = 2 O A_{1} = m_{0}

és

B M ∥ M' C

, mert tükörképek

A_{1}

-re, de

M' C ⊥ A C

, mert

A M'

átmérő

k

-ben. Így

A M

is,

B M

is magasságvonal,

M

tehát az

A B C

háromszög magasságpontja.
A háromszög létrejön, ha az

r

3 s_{0} / 2

m_{0} / 2

távolságokra teljesülnek a háromszög-egyenlőtlenségek, megengedve az egyenlőség jelét is, mert

A

O

és

S

egy egyenesen is lehetnek (egyenlő szárú háromszög esetén), továbbá ha

O A_{1} = m_{0} / 2 < r

A_{1}

k

belsejében van. Megengedhetjük az

m_{0} = 0

esetet is, ami az

A

-ban derékszögű háromszögeket adja, ekkor azonban

s_{0} = 2 r / 3

kell hogy legyen, és a feladat határozatlanná válik, minden

2 r

átfogójú derékszögű háromszög megoldása.

Megjegyzés. Az

A M M'

háromszögnek

M O

is súlyvonala, így átmegy

S

-en és

M S : S O = 2 : 1

. Eszerint egy háromszög magasságpontja, súlypontja és körülírt körének középpontja egy egyenesen van ebben a sorrendben, és a súlypont a másik két pont közti szakasznak a körülírt kör középpontja felőli harmadoló pontja. Ezt az egyenest nevezik a háromszög Euler-egyenesének. Ha megfordítva, ezt a tételt ismerjük, ebből könnyen adódik az

O A_{1} = m_{0} / 2

összefüggés és a fenti szerkesztés.