Feladat: F.1671 Korcsoport: 14-15 Nehézségi fok: átlagos
Füzet: 1970/február, 51 - 52. oldal  PDF  |  MathML 
Témakör(ök): Nevezetes azonosságok, Másodfokú (és arra visszavezethető) egyenletrendszerek, Paraméteres egyenletrendszerek, Polinomok szorzattá alakítása, Feladat
Hivatkozás(ok):Feladatok: 1969/szeptember: F.1671

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Az adottakból kivonással adódó

x2-y2=(a-b)(x-y)
egyenletet akár (1)-gyel, akár (2)-vel összekapcsolva az eredetivel ekvivalens rendszert kapunk. Újabb alakítással
(x-y)(x+y-a+b)=0,
ami két módon teljesül:
A)   ha    x-y=0,B)   ha   x+y-a+b=0.  

Az A) esetben y=x, és ezt (1)-behelyettesítve
x2=(a+b)x,x(x-a-b)=0,
amiből az eredeti rendszer két megoldása:
x1=y1=0,x2=y2=a+b.(3)

A B) esetben
x+y=a-b,y=(a-b)-x,(4)
és ezt (1)-be helyettesítve
x2-(a-b)x-b(a-b)=0,(5)
amiből újabb két megoldás számára
x3=12(a-b-(a-b)(a+3b)),(6')x4=12(a-b+(a-b)(a+3b)),
és mivel (4) és (5) szerint egyaránt
x3+y3=x4+y4=x3+x4=a-b,
azért
y3=x4,y4=x3.(6'')
Ezzel az egyenletrendszert megoldottuk.
 

II. A (3) megoldások minden (valós) a, b értékpár esetén valósak, (6') és (6'') pedig akkor és csak akkor, ha a négyzetgyökjel alatti zárójeles tényezők előjele nem ellentétes; részletezve, ha vagy egyikük sem negatív:
a-b≧0ésa+3b≧0,
azaz
a>0és-a3≦b≦a,
vagy ha mindkét zárójelben negatív szám áll:
a-b<0ésa+3b<0,
azaz
a<0ésa<b<-a3.

III. Ugyanezek felhasználásával azt is kapjuk, hogy mind a négy megoldás valós és különböző, ha
a>0és-a3<b<a,vagy haa<0ésa<b<-a3;
ugyanis ezen egyenlőtlenségek teljesülése esetén a diszkrimináns pozitív, x3≠x4=y3, ugyanígy x4≠y4 és ezek a (3) megoldásoktól is különbözők, mert azokban x=y; továbbá a (3) alattiak egymástól is különbözők, mert az egyenlőtlenségek miatt b≠-a, és így x2=a+b≠0=x1 (1. ábra).
 

 
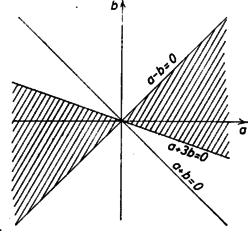1. ábra
 

x3=x4 (és vele y3=y4) kétféleképpen adódhat:
α) ha a-b=0, ekkor azonosak az x1=y1=0 megoldással, ezért a rendszernek 2 megoldása van, ha a≠0, és egyetlen megoldása, ha a=0.
β) ha pedig a+3b=0, ekkor azonosak az x2=y2=a+b megoldással, 2 megoldás van, ha a≠0.
 

Megjegyzés. Ha b≠0, akkor (1) is, (2) is a derékszögű koordinátarendszerben egy-egy parabola egyenlete, és ezek egymás tükörképei a tengelyek közti, y=x, azaz y-x=0 egyenletű szögfelezőre nézve, hiszen x és y felcserélésével a két egyenlet átmegy egymásba. Így a rendszer megoldásai e két parabola legföljebb 4 közös pontjának koordinátái. Az (x1,y1) és (x2,y2) megoldások rajta vannak a tükrözés tengelyén. Az (x3,y3), (x4,y4) megoldásokat összekötő, (4) egyenletű egyenes pedig merőleges a tükrözés tengelyére.