Kezdőlap


Feladat:	F.1670	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bajmóczy E. , Balogh Zoltán , Donga Gy. , Gajdács Ibolya , Gegesy F. , Göndőcs F. , Hadik R. , Kóczy L. , Komjáth P. , Lukács P. , Nagy Ferenc , Papp Z. , Sailer K. , Somorjai G. , Szalontai Á.
Füzet:	1969/november, 133 - 135. oldal		PDF \| MathML
Témakör(ök):	Poliéderek átdarabolása, Feladat
Hivatkozás(ok):	Feladatok: 1969/május: F.1670

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A kívánt kocka térfogata egyenlő az adott kockák együttes térfogatával, $2 m^{3}$ -rel, ezért egy élének hossza $c = \sqrt[3]{2} m$ , $0, 1 mm$ -nél kisebb hibával $1, 26 m$ .
Illesszük össze a két kockát $2 m$ hosszú, $1 m$ széles és $1 m$ magas téglatestté. Ezt magasságának változatlanul hagyásával $c$ szélességű és $c^{2}$ hosszúságú téglatestté daraboljuk át (ami ált al alapjának területe $c^{3} = 2$ , változatlan marad), majd $c$ szélességének változatlanul hagyásával $c$ hosszúságú és $c$ magasságú téglatestté daraboljuk, vagyis kockává, ennek során előlapjának területe $(1 \cdot c^{2} = c \cdot c)$ marad változatlan.
Mindkét téglalap-átdarabolás többféleképpen végezhető; adott és előírt méretek esetére az 1200. gyakorlatban¹ két lehetőséget láttunk: I. a téglalap oldalaihoz képest csupa ferde vágással, egy közbülső paralelogrammába való átdarabolással, ill. II. egy vágást a téglalap oldalaival párhuzamosan végezve. Alább az utóbbi szerint írunk le egy átdarabolást.
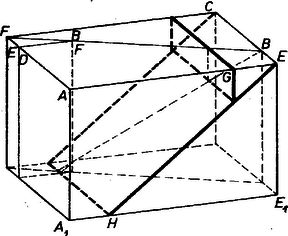
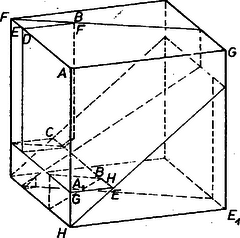
Az $A B C D$ fedőlap $A B = C D = 2 m$ oldalaira felmérjük az $A E = C F = c^{2} (\approx 1, 5874)$ szakaszokat, a téglatestet kettévágjuk a $B F$ szakaszon átmenő függőleges ( $A B C D$ -re merőleges) sík mentén, továbbá az $A B F D$ trapéz alapú hasábot az $E$ -n átmenő, $A B$ -re merőleges (ugyancsak függőleges) síkkal.

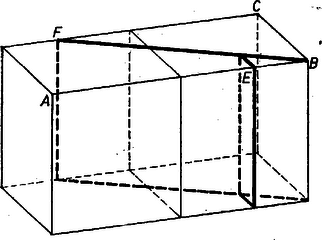
Az utóbbi vágás adta kis

3

oldalú hasáb darabot a

B F

vektorral toltuk el, az első vágással létrejött

B C F

alapú hasábot pedig

B F

irányban úgy, hogy

F

csúcsa az

A D

egyenesbe jusson (az ábra két felső része).
Lényegében ugyanígy végezzük a darabolást és átrendezést az ábra jobb felső részéből az alsóba, miután az

A E E_{1} A_{1}

előlap

A E = E_{1} A_{1} = c^{2}

éleire felmérjük az

A G = E_{1} H = c

szakaszokat és a téglatestet elvágjuk az előlapra merőleges síkkal

E H

mentén, majd a trapéz alapú darabot még

G

-n át is az

A E

-re merőleges síkkal.

A leírt eljárás helyes voltának bizonyítását az olvasóra hagyjuk.
Az első metszéspár útján keletkezett

3

rész-test mindegyike két részre esik szét az utóbbi pár első metszése útján, az utolsó metszés viszont csak

2

régebbi darabot vág ketté, így az (összeillesztett) téglatestet

8

darabra vágtuk el.

Nagy Ferenc (Budapest, I. István Gimn., III. o. t.)

Balogh Zoltán (Debrecen, Fazekas M. Gimn., I. o. t.)

Megjegyzés. Többen a két adott kockát külön-külön

c

c

c / 2

méretű négyzetes oszloppá darabolták át és ezeket tették össze

c

élű kockává. ‐ A két db

1 m^{3}

-es kockából egy kocka szerkesztése az ún.déloszi probléma. Ezt több megoldó is megjegyezte.
A leírt eljárás

c^{2}

és

c

felmérése miatt természetesen csak közelítő eljárás.

¹K. M. L. 38 (1969) 158. o.