Kezdőlap


Feladat:	F.1668	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Baintner L. , Bajmóczy E. , Beck J. , Chikán B. , Csetényi A. , Dombi G. , Donga Gy. , Fischer Ágnes , Gál P. , Hadik R. , Kemény A. , Kóczy L. , Legeza L. , Lukács P. , Maróti P. , Papp Z. , Pintér I. , Reviczky J. , Sailer K. , Simon Júlia , Szabó Gy. , Szalontai Á. , Terjéki J. , Török I. , Várhegyi Éva , Viszkei Gy.
Füzet:	1970/január, 13 - 16. oldal		PDF \| MathML
Témakör(ök):	Egyenesek egyenlete, Parabola egyenlete, Kúpszeletek érintői, Parabola, mint kúpszelet, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1969/május: F.1668

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Válasszuk úgy a koordinátarendszert, hogy origója a közös fókusz legyen, és az első parabola tengelye legyen az $y$ tengely. Ekkor az első parabola vezéregyenese az $y = - p$ egyenes, egyenlete

\begin{matrix} x^{2} + y^{2} = {(y + p)}^{2} \end{matrix}

(a bal oldalon a fókusztól, a jobb oldalon a vezéregyenestől mért távolság négyzete áll), avagy

\begin{matrix} y = \frac{x^{2} - p^{2}}{2 p} . \end{matrix}

(1)

x_{0}

ponthoz tartozó érintő meredeksége a függvény

x_{0}

-beli differenciálhányadosával egyenlő:

x_{0} / p

, a parabola megfelelő érintőjének egyenlete:

\begin{matrix} y - \frac{x_{0}^{2} - p^{2}}{2 p} = \frac{x_{0}}{p} (x - x_{0}), \end{matrix}

ahonnan rendezéssel:

\begin{matrix} x_{0} x - p y - \frac{x_{0}^{2} + p^{2}}{2} = 0. \end{matrix}

(2)

Mivel a két parabola tengelye merőleges egymásra, a második parabola tengelye az

x

tengelyen van, egyenlete a fentiekhez hasonlóan

\begin{matrix} x = \frac{y^{2} - q^{2}}{2 q}, \end{matrix}

(3)

ahol

q

a fókusz és a vezéregyenes távolsága, és az

y_{0}

ordinátájú ponthoz tartozó érintő egyenlete

\begin{matrix} - q x + y_{0} y - \frac{y_{0}^{2} + q^{2}}{2} = 0. \end{matrix}

(4)

A (2) és (4) egyenletek csak akkor határozzák meg ugyanazt az egyenest, ha egyik a másiknak valamely konstansszorosa:

\begin{matrix} x_{0} = - λ q; - p = λ y_{0}; \frac{x_{0}^{2} + p^{2}}{2} = λ \frac{y_{0}^{2} + q^{2}}{2}, \end{matrix}

ahonnan a

λ

konstansra a

\begin{matrix} (p^{2} + q^{2} λ^{2}) (λ - 1) = 0 \end{matrix}

egyenletet kapjuk, és ennek egyetlen valós megoldása

λ = 1

, ekkor

x_{0} = - q

y_{0} = - p

, tehát a közös érintő egyenlete:

\begin{matrix} q x + p y + \frac{p^{2} + q^{2}}{2} = 0. \end{matrix}

(5)

Feladatunk első állítását ezzel bebizonyítottuk.
Tekintsük most a két parabola egy-egy érintőjét. (2) és (4) alapján ezek csak akkor merőlegesek egymásra, ha

\begin{matrix} q x_{0} + p y_{0} = 0, \end{matrix}

(6)

ekkor a két egyenes metszéspontja az

\begin{matrix} M (\frac{x_{0} - q}{2}, \frac{y_{0} - p}{2}) \end{matrix}

pont, mely rajta van az (5) egyenesen.
Így tulajdonképpen feladatunk állításának a fordítottját láttuk be: a merőleges érintők metszéspontja az (5) alatti közös érintőn van. A fenti lépéseket fordított sorrendben elvégezve kapjuk a kívánt bizonyítást. Az (5) egyenes tetszőleges

M (x_{1}, y_{1})

pontjához válasszuk meg

x_{0}

y_{0}

értékét úgy, hogy

\begin{matrix} \frac{x_{0} - q}{2} = x_{1}, \frac{y_{0} - p}{2} = y_{1} \end{matrix}

teljesüljön: az így kapott (2) és (4) egyenesek átmennek

M

-en és merőlegesek egymásra.

II. megoldás. Megmutatjuk, hogy egy parabola

P

pontján átmenő érintő azonos

P

-nek a vezéregyenesen levő

Q

vetülete és az

F

fókusz közti

F Q

szakasz felező merőlegesével. Valóban, az I. megoldás (2) egyenlete által meghatározott

Q

koordinátái

(x_{0}, - p)

, az

F Q

szakasz felezőpontja

(\frac{x_{0}}{2}, - \frac{p}{2})

,ez rajta van a (2) alatti érintőn, és az

F Q

egyenes egyenlete

\begin{matrix} p x + x_{0} y = 0, \end{matrix}

ez tehát merőleges (2)-re.
Esetünkben a két parabola tengelyének merőleges volta miatt

d_{1}

d_{2}

vezéregyeneseik is merőlegesek, és közös

D_{12}

pontjukat véve a mondott tételben

Q

szerepére,

F D_{12}

-nek

m

felező merőlegese ‐ ahol

F

a két parabola közös fókuszát jelöli ‐ mindkét parabolát érinti (1. ábra).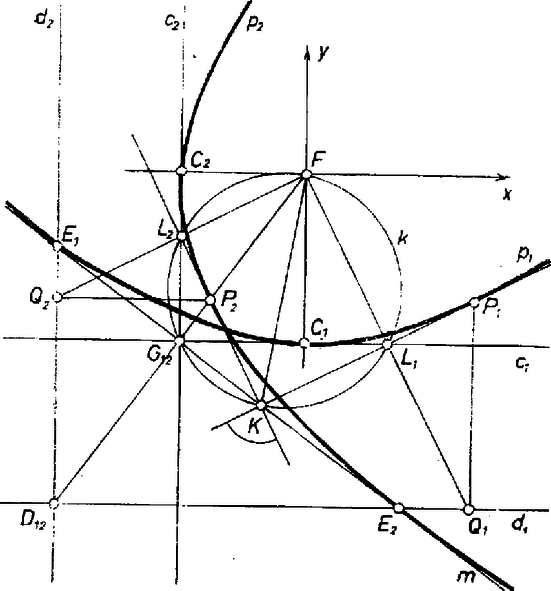

1. ábra

(Az is következik innen, hogy

m

d_{1}

vezéregyenesű parabolát a

d_{2}

-vel való metszéspontban érinti; a

d_{2}

vezéregyenesű parabolát pedig a

d_{1}

-gyel való metszéspontjában.)
Ha bizonyítás nélkül elfogadjuk, hogy a fenti

Q

-t

d

-n végigfuttatva a parabola minden érintőjét megkapjuk, akkor az állítás megfordítása így mondható ki: a parabola fókuszának bármely érintőre vett tükörképe rajta van a vezéregyenesen. Ebből következik, hogy két parabolánknak nincs további közös érintője.
Ismét más megfogalmazása a mondott tulajdonságnak a kővetkező: az

F Q

szakasz

G

felezőpontjából minden olyan szakasz derékszögben látszik, melynek egyik végpontja

F

, másik pedig a

t

érintő valamely (

G

-től különböző) pontja. És mivel a

G

pontok összessége a

d

-nek

F

-ből a felére kicsinyített

c

képe ‐ a parabola ún. csúcsérintője ‐, azért tetszőleges

K

külső pontból a parabolához húzható érintőknek a

c

-n levő pontjait az

F K

átmérőjű Thalész-körrel metszhetjük ki.
Eszerint

K

-t az

m

közös érintőn bárhol véve, a

k

Thalész-kör mindig átmegy

F D_{12}

-nek

G_{12}

felezőpontján, ami egyszersmind a

c_{1}, c_{2}

csúcsérintők közös pontja. Ezeknek

k

-val való második közös pontját

L_{1}, L_{2}

-vel jelölve a

K

-ból húzott második érintők közti szög a kerületi szögek tétele és Thalész tétele alapján

\begin{matrix} L_{1} K L_{2} ∢ = L_{1} G_{12} L_{2} ∢ = 90^{\circ}, \end{matrix}

hiszen a csúcsérintők szöge egyenlő a vezéregyenesek, valamint a parabolatengelyek közti szöggel. Az állítást bebizonyítottuk.

\begin{matrix} * \end{matrix}

A parabola felhasznált tulajdonsága megtalálható a gimnáziumok III. osztályaiban az 1967‐68. tanév végéig használatban volt tankönyvben¹. Ott a parabolát az

y = x^{2}

egyenlet képeként értelmezték, az érintőt pedig így: az érintő a szelő határhelyzete, amikor a szelőnek és a görbének két metszéspontja egybeesik, és ezekből elemezték ki, hogy a parabola egyszersmind azoknak a pontoknak a mértani helye, amelyek egy adott ponttól ugyanakkora távolságra vannak, mint egy adott egyenestől.
A gimnázium III. osztályának jelenlegi tankönyve viszont a parabolát a most mondott mértani helyként értelmezi, az érintőt pedig (burkoltan) ugyancsak a fenti módon, de csak iránytangensének megállapítására ad eljárást (differenciálható függvényeket ábrázoló görbék eseteire); ezért az alábbiakban inkább elemi úton és koordináták mellőzésével bizonyítjuk a parabola felhasznált tulajdonságát.
Az

F Q

szakasz

m

felező merőlegesének és a

d

-re

Q

-ban emelt merőlegesnek

P

metszéspontja parabolapont, hiszen

P F = P Q

, és

P Q

P

-nek

d

-től mért távolsága. Eszerint a

P

középpontú,

F

-en átmenő

k

kör érinti

d

-t, éppen

Q

-ban. A parabolának

m

-en

P

az egyetlen pontja, mert

m

-nek egy

P

-től különböző

P_{1}

pontjára

P_{1} F = P_{1} Q

, az utóbbi viszont nagyobb

P_{1}

-nek

d

-től mért távolságánál, hiszen

P_{1} Q

nem merőleges

d

-re (2. ábra).

2. ábra

Ha viszont

m

-et

P

körül elfordítjuk az

m^{*}

helyzetbe,

m^{*}

-on van még egy

P^{*}

parabolapont, vagyis olyan, hogy a

P^{*}

közepű,

F

-en átmenő

k^{*}

kör érinti

d

-t egy

Q^{*}

pontban. Azt állítjuk, hogy

Q^{*}

Q

tükörképe arra a

H

pontra nézve, amelyet az

F

-ből

m^{*}

-ra bocsátott merőleges metsz ki

d

-ből. Messe

F H

k

-t

F^{*}

-ban. Ekkor a

H

-ból

k

-hoz húzott érintő és szelő alapján

H Q^{2} = H F^{*} \cdot H F

. a tükrözés miatt

H Q^{* 2} = H Q^{2}

, tehát

H Q^{* 2} = H F^{*} \cdot H F

, vagyis az

F, F^{*}, Q^{*}

pontokon átmenő kört

d

érinti

Q^{*}

-ban. E kör középpontja

F F^{*}

felező merőlegesén van, ami a szerkesztés szerint

m^{*}

, másrészt a

Q^{*}

-ban

d

-re emelt merőlegesen, tehát

P

-től különböző pont (hiszen

H

, és így

Q^{*}

is különböző

Q

-tól), ez a mondott

P^{*}

.
Ezek szerint

m^{*}

-ot

m

felé forgatva, amikor egybeesik

m

-mel, akkor

H

és

Q^{*}

egybeesik

Q

-val,

P^{*}

pedig

P

-vel, tehát

m

valóban a parabola érintője.
Eredményünkből az is következik, hogy a

P

-beli érintő egyszersmind az

F P Q ∢

szögfelezője, tehát az állítás felhasznált megfordítása is helyes volt.

¹Gallai T.-Hódi E.-Péter R.-Szabó P.-Tolnai J.: Matematika a gimn. III. o. számára, 9. kiadás, Tankönyvkiadó, Budapest, 1959. 203‐209. o.