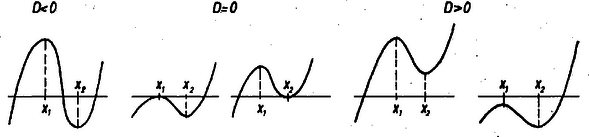|
| Feladat: |
F.1661 |
Korcsoport: 18- |
Nehézségi fok: nehéz |
| Megoldó(k): |
Balogh Z. , Birkner L. , Csetényi A. , Divinyi S. , Eller J. , Gegesy Ferenc , Gerhardt T. , Horváth Miklós , Kálmán M. , Kemény A. , Kérchy L. , Krasznai A. , Lázár A. , Lengyel J. , Lévai G. , Lukács P. , Papp Z. , Pressing L. , Prőhle T. , Sailer K. , Somorjai G. , Szalay Csilla , Szalontai Á. , Tarsó B. , Viszkei Gy. , Walthier T. |
| Füzet: |
1969/november,
129 - 132. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Szélsőérték differenciálszámítással, Függvényvizsgálat differenciálszámítással, Függvényvizsgálat, Feladat |
| Hivatkozás(ok): | Feladatok: 1969/április: F.1661 |
|
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. A függvénynek csak ott lehet szélső értéke, ahol deriváltja eltűnik: vagyis az helyeken. Ezek akkor és csak akkor valósak és különbözők, ha ( esetén , tehát a szélső értékek eleve nem lehetnek különböző előjelűek).
E feltétel teljesülése esetén az helyek mindegyikén van is szélső érték, mert előjelet vált, -en (ami ) áthaladva pozitívból negatívvá válik, hiszen itt csökken, -n áthaladva pedig negatívból pozitívvá, így az függvénynek -ben (helyi) maximuma és -ben (helyi) minimuma van.
A szélső értékek:
és ezek akkor és csak akkor ellentett előjelűek, ha szorzatuk negatív: | | (2) |
Ez a feltétel magában foglalja (1)-et is, hiszen esetén a bal oldal így szélső értékei akkor és csak akkor ellentett előjelűek, ha a , együtthatókra teljesül a (2) feltétel.
| Gegesy Ferenc (Budapest, Móricz Zs. Gimn., IV. o. t.) |
Megjegyzés. Akik ismerik az redukált harmadfokú egyenlet megoldóképletét, azok (2) szögletes zárójelében felismerik az egyenlet diszkriminánsát. Ezt a megoldás diszkussziójával egybevetve látjuk, hogy szélső értékei ellentett előjelű voltának feltétele azonos azzal, hogy az egyenletnek három különböző valós gyöke legyen. Valóban, a fentebbiek szerint az értékekre , az -et ábrázoló görbe süllyed, , így és ellentétes jelű volta azt jelenti, hogy és , a görbének a maximum előtti, emelkedő szakasza, továbbá az és közti, süllyedő szakasza, végül a minimum utáni, emelkedő szakasza külön-külön metszik az tengelyt, innen a különböző valós gyök.
A feltételek megfeleltetését folytatva | |
azt jelenti, hogy a szélső értékek egyike , a görbe itt érinti az tengelyt, kétszeres gyök van, ill. hogy a két szélső érték egyenlő előjelű (vagy mindkettő pozitív, vagy mindkettő negatív). Az ábra a görbe menetét vázolja esetére, előjele szerint.
II. megoldás. Az függvény képét az függvény képéből -val való eltolással kapjuk az tengely irányában, emiatt először az egyszerűbb függvényt vizsgáljuk. Mivel , azaz a függvény ún. páratlan függvény, elegendő pozitív -ekre vizsgálnunk. Három esetet különböztetünk meg:
1. Ha , akkor két monoton növekvő függvény összege, tehát is monoton nő, így nincsenek szélső értékei.
2. Ha , akkor , ismét monoton növekvő.
3. Ha , mondjuk (ahol ), akkor így a intervallumon negatív, mellett pozitív. mellett mindhárom tényező pozitív és monoton nő, így is nő, ezért szélső érték csak a szakaszon lehet. Ezt a számtani és mértani közép ismert nagyságviszonya alapján akarjuk meghatározni. Alakítsuk (3)-at így: | |
ahol -t és -t úgy akarjuk meghatározni, hogy a három tényező összege állandó legyen. Ekkor ugyanis a szorzat akkor maximális, ha tényezői egyenlőek. Ha az összegben együtthatója eltűnik: akkor az összeg állandó, és a tényezők egyenlőek, ha még
is teljesül. Ennek az egyenletrendszernek egy megoldása pl. | |
(és teljesül ), tehát -nek mellett van minimuma, és itt a függvény értéke | |
Mivel páratlan, ebből a függvény lokális maximuma is előállítható:
Visszatérve az függvényre, ennek is csak negatív mellett lesz szélső értéke, és ezek akkor lesznek különböző előjelűek, ha értéke és közé esik, azaz | |
ami természetesen csak negatív -re teljesülhet, ez tehát a szükséges és elegendő feltétele annak, hogy az függvény szélső értékei különböző előjelűek legyenek.
Kissé más alakban lásd Hack Frigyes: Függvénytáblázatok, matematikai összefüggések, Tankönyvkiadó, Budapest, 1967, 61‐62. o. |
|
 PDF |
PDF |  MathML
MathML