Kezdőlap


Feladat:	F.1660	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Hetzer Jenő
Füzet:	1969/november, 128 - 129. oldal		PDF \| MathML
Témakör(ök):	Egyenesek egyenlete, Parabola egyenlete, Kúpszeletek érintői, Feladat
Hivatkozás(ok):	Feladatok: 1969/április: F.1660

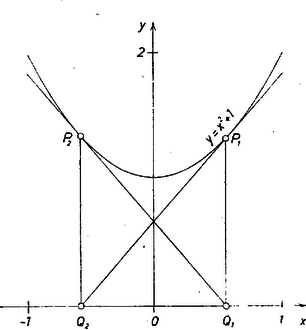
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyenek a $P_{1}$ pont koordinátái $(x_{1}, y_{1})$ . Mivel $P_{1}$ a parabolán van, $y_{1} = x_{1}^{2} + 1$ . A $P_{1}$ ponton átmenő érintő $m$ meredeksége az

\begin{matrix} f (x) = x^{2} + 1 \end{matrix}

függvény

x_{1}

-beli differenciálhanyadosával egyenlő:

\begin{matrix} m = f' (x_{1}) = 2 x_{1} . \end{matrix}

Az érintő egyenlete eszerint

\begin{matrix} y = 2 x_{1} (x - x_{1}) + y_{1} . \end{matrix}

Ez az egyenes az

x

tengelyt az

\begin{matrix} x = \frac{2 x_{1}^{2} - y_{1}}{2 x_{1}} = \frac{x_{1}^{2} - 1}{2 x_{1}} \end{matrix}

abszcisszájú pontban metszi.

Feladatunk szerint ez a metszéspont azonos a parabola

P_{2} (x_{2}, y_{2})

pontjának az

x

tengelyen levő

Q_{2} (x_{2},0)

vetületével, ezért

\begin{matrix} x_{2} & = \frac{x_{1}^{2} - 1}{2 x_{1}}, azaz \\ 2 x_{1} x_{2} = x_{1}^{2} - 1. & (1) \end{matrix}

P_{1}

P_{2}

pontok szerepének felcserélésével kapjuk annak feltételét, hogy a

P_{2}

beli érintő átmenjen a

Q_{1} (x_{1},0)

ponton:

\begin{matrix} 2 x_{2} x_{1} = x_{2}^{2} - 1. \end{matrix}

(2)

A bal oldalak egyenlők, tehát a jobb oldalak is. Ebből

x_{1}^{2} = x_{2}^{2}

. Nyilván nem lehet azonban

x_{1} = x_{2}

, azaz

P_{1}

és

P_{2}

azonos, tehát

x_{2} = - x_{1}

, amit (1)-be helyettesítve kapjuk, hogy

\begin{matrix} - 2 x_{1}^{2} = x_{1}^{2} - 1, \end{matrix}

azaz

x_{1} = \pm 1 / \sqrt[]{3}

. Ezek szerint a függvénygörbe

\begin{matrix} P_{1} (\pm 1 / \sqrt[]{3}, 4 / 3) és P_{2} (\mp 1 / \sqrt[]{3}, 4 / 3) \end{matrix}

pontjai felelnek meg a követelménynek. A két lehetséges előjel-választás tehát csak a pontok szerepének felcserélését jelenti, így lényegében egyetlen megoldása van a feladatunknak.

Hetzer Jenő (Sopron, Széchenyi I. Gim., III. o. t.)