Feladat:	F.1657	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Beck J. ,  Eller J. ,  Fiscer Ágnes ,  Gegesy F. ,  Göndőcs F. ,  Lukács P. ,  Maróti György ,  Simon Júlia ,  Szalontai Á.
Füzet:	1970/április, 149 - 151. oldal		PDF  |  MathML
Témakör(ök):	Trigonometriai azonosságok, Egyenlő szárú háromszögek geometriája, Érintőnégyszögek, Koszinusztétel alkalmazása, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1969/március: F.1657

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.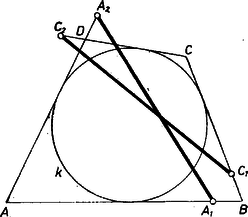   1. ábra   a) A szerkesztés szerint $A{A}_1{A}_2$ egyenlő szárú háromszög, így (1. ábra) 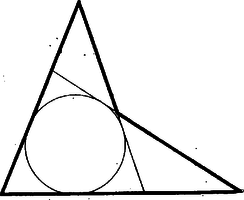${\displaystyle \begin{array}{ccc}\hfill {\displaystyle A_{1}A{}_2^2=}& {\displaystyle 4AA{}_2^2\text{sin}{}^2\frac{A_{1}A{A}_2\sphericalangle }{2}=4AB\cdot AD\text{sin}{}^2\frac{BAD\sphericalangle }{2}=2AB\cdot AD\left(1-\text{cos}BAD\sphericalangle \right)\mathrm{,}}\hfill & \text{(<mn>1</mn>)}\end{array}}$ és a cosinustétel alkalmazásával $\begin{array}{c}{\displaystyle A_{1}A{}_2^2=2AB\cdot AD-\left(A{B}^2+A{D}^2-B{D}^2\right)=B{D}^2-{\left(AB-AD\right)}^2\mathrm{.}}\end{array}$ (2) Hasonlóan a $C{C}_1{C}_2$ egyenlő szárú háromszögből és a cosinustételt a $BCD$ háromszögre alkalmazva $\begin{array}{c}{\displaystyle C_{1}C{}_2^2=2CB\cdot CD\left(1-\text{cos}BCD\sphericalangle \right)=B{D}^2-{\left(CB-CD\right)}^2\mathrm{.}}\end{array}$ (3) És mivel $k$ belülről érinti négyszögünk oldalait, azért $\begin{array}{c}{\displaystyle AB+CD=BC+AD\mathrm{,}}\end{array}$ innen $\begin{array}{c}{\displaystyle AB-AD=CB-CD\mathrm{,}}\end{array}$ (4) tehát (2) és (3) jobb oldalai egyenlők. igy pedig $A_1{A}_2=C_1{C}_2$, hiszen szakaszok hossza pozitív.     2. ábra   b) Ha $k$ nincs az $N$ belsejében, akkor azokban a háromszögekben sincs benne, amelyeket $N$ egy‐egy oldalának elhagyásával kapunk, így $k$ bármelyik ilyen háromszögnek külső érintő köre. Nem nehéz belátni, hogy csak a 3. ábra a) és b) részén látható típusú helyzetekkel kell foglalkoznunk (mert a 2. ábra típusában $k$ benne van a konkáv 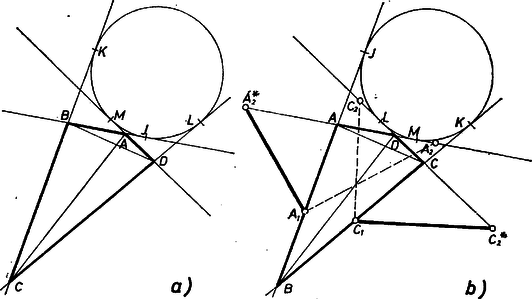$N$-ben).     3. ábra   Foglalkoznunk kell mind a két esettel. Mert bár igaz, hogy a 3a) és 3b) ábrák csupán betűzésben különböznek: az a) ábrán $k$ az $A$ és $C$ szögeknek a tartományában, ill. a csúcsszögtartományában van benne, a $B$ és $D$ szögeknek pedig a mellékszögtartományában, és a b) ábra ebből az $A\mathrm{,}$ $C$ és $B\mathrm{,}$ $D$ betűpárok felcserélésével keletkezett, a feladat szempontjából viszont az $A\mathrm{,}$ $C$ pár szerepe és a $B\mathrm{,}$ $D\mathrm{,}$ páré egymástól különböző. A 3a) ábra esetében az állítás érvényes marad, mert a bejelölt érintési pontok felhasználásával a (2)-beli különbség, az egyes csúcsokból húzott érintőszakaszok egyenlőségét felhasználva, egyenlőnek adódik a (3)-beli különbség $\left(-1\right)$-szeresével: ${\displaystyle \begin{array}{c}\hfill {\displaystyle AB-AD=\left(JB-JA\right)-\left(MD-MA\right)=KB-LD=\left(KC-BC\right)-\left(LC-DC\right)=CD-CB\mathrm{,}}\hfill \end{array}}$ tehát fenti záró következtetésünk érvényes. Ebben a helyzetben ezt találtuk: $\begin{array}{c}{\displaystyle BA+BC=DA+DC\mathrm{,}}\end{array}$ és ez a 3b) ábra betűzése szerint a következőbe megy át: $\begin{array}{c}{\displaystyle AD+AB=CD+CB\mathrm{,}}\end{array}$ (5) ennek alapján pedig a (2) és (3)-beli különbségekre semmit sem mondhatunk ki, ebben az esetben a feladat állítása általában nem marad érvényben (deltoid esetében megmarad, de ennek szimmetriája miatt semmitmondó). Eredményeink így is kimondhatók: ha az $AB\mathrm{,}AD$ egyenesek egyike sem választja szét a kört és a négyszöget, vagy mindegyike szétválasztja, akkor az állítás érvényes ‐ és ekkor $CB$-hez is, $CD$-hez képest is $k$ és $N$ egyformán helyezkednek el ‐, ha pedig $AB$ és $AD$ egyike elválasztja $k$-t $N$-től, a másika nem, akkor az állítás nem érvényes. Csekély módosítással viszont érvényes lesz az állítás a 3b) ábra esetére is. A (2) zárójelében álló mínusz jel az (1)-beli mínusz jelből öröklődött át, így az (5) bal oldalán álló plusz jelet úgy használhatnók fel, ha (1)-ben is plusz jel állna, más szóval, ha a $BAD$ szög mellékszögét használjuk fel. Ez azt jelenti, hogy pl. $A{A}_1$-et $B$ felé, $A{A}_2$-t pedig a $D$-vel ellentétes irányban felmérve ─ és persze (3)-ra tekintettel ugyanígy $C{C}_2$-t a $D$-vel ellentétes irányban ‐ az állítás érvényessé válik a 3b) ábra esetében is.   Maróti György (Győr, Czuczor G. Bencés Gimn., III. o. t.) dolgozata alapján, kiegészítésekkel