Feladat: F.1652 Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Donga György ,  Kóczy L. ,  Nagy Ferenc ,  Prőhle Tamás ,  Somorjai Gábor 
Füzet: 1969/november, 117 - 121. oldal  PDF  |  MathML 
Témakör(ök): Gömbi geometria, Kombinatorikai leszámolási problémák, Szögfüggvények a térben, Feladat
Hivatkozás(ok):Feladatok: 1969/február: F.1652

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az XX' átmérőn átmenő fél-főkörre az α=180∘/15=12∘-os szög többszöröseit kell felmérnünk. A kapott osztópontok szimmetrikusak az XX' átmérőre merőleges, O-n átmenő S1 síkra, így a belőlük származtatott körök is szimmetrikusak S1-re (1. ábra).

 

 

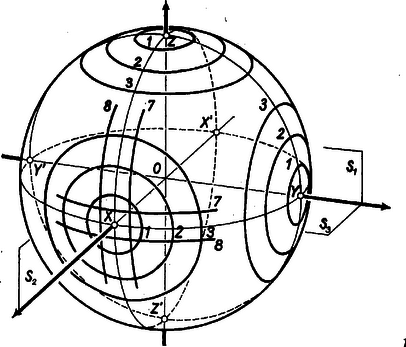1. ábra
 

Hasonlóan szimmetrikusak az YY', ZZ' tengelyekhez tartozó körök a tengelyekre merőleges S2, ill. S3 síkra. Ez a három sík a teret és a gömböt 8 részre vágja fel, a fenti szimmetria miatt elegendő e részek egyíkét megvizsgálni, az itt talált metszéspontoknak az összes többiben megtaláljuk a megfelelőit a határoló síkokra való tükrözés útján.
Tegyük fel, hogy a megrajzolt körök közül három megy át a gömb választott nyolcadának valamely P pontján. Tartozzék ez a három kör rendre az α szög k-, l-, m- szereséhez, ahol feltevésünk szerint k, l, m 1 és 7 közötti egész számok.
 

 

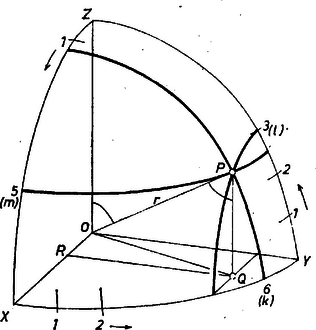2. ábra
 

Legyen P vetülete az S3 síkon Q, az OPQ derékszögű háromszögben OPQ∢=POZ∢=mα, emiatt (2. ábra)
PQ=rcosmα,
ahol r a G gömb sugara. Hasonlóan
QR=rcoslα,OR=rcoskα,
ahol R a Q pontnak az XX' egyenesen levő vetülete. Az OQR, OQP derékszögű háromszögekben
OP2=OQ2+QP2=OR2+RQ2+QP2,
tehát
cos2kα+cos2lα+cos2mα=1.(1)
Ezek szerint meg kell keresnünk az (1) egyenlet gyökeit. Ennek érdekében meghatározzuk az α szög többszöröseinek a cosinusát, illetve a
cos2β=(cos2β+1)/2
összefüggés alapján a 2-szeresük cosinusából közvetlenül e cosinusok négyzetét, a táblázat alapján:
 


β12∘24∘36∘48∘60∘72∘84∘|cos2β0,95680,83460,65450,44770,25000,09550,0109
 

Ha az (1)-ben szereplő három szög közül a legkisebb 12∘-os volna, akkor a másik két cosinus négyzetösszegének
1-0,9568=0,0432
-nek kellene lennie, e szögek tehát csak 84∘-osak lehetnének, mert cosinus-négyzetük külön-külön legfeljebb 0,0432; így látnivalóan nem kapunk gyököt.
Ha a legkisebb szög 24∘-os, a másik két szögre jutó maradék 0,1654, csak 72∘-os és 84∘-os szögek jöhetnének szóba, ismét nincs megoldás.
Ha a legkisebb szög 36∘-os, a maradék 0,3455, így 60∘-os, 72∘-os, 84∘-os szögek szerepelhetnek még: az első kettő cosinusa négyzetének összege épp 0,3455.
Ha a legkisebb szög 48∘-os, a maradék 0,5523, így 48∘-os, 60∘-os, 72∘-os, 84∘-os lehet a másik kettő: egy 48∘-os és egy 72∘-os majdnem egfelel, az összeg 0,5432, tehát a hozzájuk tartozó három kör csak megközelíti egymást. Végül ha a legkisebb szög 60∘-os, akkor a cosinus-négyzetek összege legfeljebb 3⋅0,25=0,75, (1)-nek nincs ilyen megoldása.
A kapott 36∘-os, 60∘-os, 72∘-os  szöghármas valóban gyöke (1)-nek (és nem csak a táblázatunk pontosságáig elégítik ki azt), hiszen
cos260∘=14,
cos236∘=cos72∘+12=12⋅5-14+12=5+38,
cos272∘=cos144∘+12=-12⋅5+14+12=3-58,
és ezek összege valóban 1. E szöghármasnak a választott nyolcadban 6 pont felel meg, hiszen a 3, 5, 6 szorzószámokat 6-féle sorrendben feleltethetjük meg a k, l, m változóknak. Ennek a 6 pontnak az összes többi nyolcadban van megfelelője, összesen tehát 48 pont van, melyen a megrajzoltak közül 3 kör megy át.
A második kérdésre térve, nem találtunk metszést az olyan körökön, amelyek a 12∘-nak 1-, 2-, 4-, ill. 7-szereséhez tartoznak, így az ilyen körök száma a szimmetriák figyelembevételével 4⋅2⋅3=24.
 

Somorjai Gábor (Budapest, I. István Gimn., III. o. t.)

Donga György (Budapest, Berzsenyi D. Gimn., II. o. t.)
 

II. megoldás. Könnyű megrajzolni a köreinkből az XYZ gömbháromszögbe eső íveknek pl. az XOY=S3 síkon levő vetületét, hiszen az első két körrendszert kimetsző síkok erre merőlegesek, és így a megfelelő negyedkörívek vetületei az OX, ill. OY sugárra merőleges fél-húrok; a 3. körrendszert kimetsző síkok pedig párhuzamosak S3-mal, ezért mindegyik ilyen kör vetülete vele egybevágó, O középpontú kör (3. ábra).
 

 

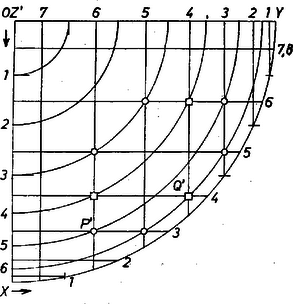3. ábra
 

Ha van a gömb felületén hármas metszéspont, annak vetületén 3 kör vetülete megy át, éspedig mindhárom körrendszer 1‐1 körének vetülete.
A rajz szerint 6 ponton látszik átmenni 3‐3 kör vetülete. Bebizonyítjuk, hogy ezek a gömbfelület olyan pontjainak vetületei, amelyeken valóban 3 kör megy át. Ezt egyetlen számítás bizonyítja, mert a pontok mindegyike az egyik körrendszer 3. körének, egy másik körrendszer 5. és a harmadik rendszer 6. körének vetületén látszik. Így pl. a XX'-re merőleges 3. és az YY'-re merőleges 6. kör vetületei közös P' pontjának OY-tól, ill. OX-től mért távolsága
cos3⋅12∘=cos36∘=5+14 ill. cos72∘=5-14, és ‐ mint az ezek négyzetösszegéből vont négyzetgyök ‐
OP'=(6+25)+(6-25)16=32=sin5⋅12∘.
Ez pedig a ZZ'-re merőleges körrendszer 5. körének sugara, ami állításunkat igazolja.
Az ilyen pontok száma valóban 6, ahányféle sorrendben a körök 3., 5. és 6. sorszámait az OX, OY, OZ tengelyű körrendszerhez hozzárendelhetjük:
(3,5,6),(3,6,5),(5,3,6),(5,6,3),(6,3,5),(6,5,3).

További 3 esetben 3 vetület csak közel halad egymáshoz: két körrendszer 4. és a harmadik rendszer 6. körének vetülete. Valóban cos4⋅12∘=cos(30∘+18∘), ehhez
cos18∘=10+254,sin18∘=5-14,  így  cos48∘=18(30+65-5+1),
de a fentiekhez hasonlóan az első két körből adódó négyzetösszeg négyzetgyöke
2cos248∘=2cos48∘≠sin6⋅12∘=10+254.
(A két oldal eltérése 3 tizedesre kerekítve 0,005).
Ezek szerint a gömbfelület 8⋅6=48 pontján megy át 3-3 kör; másrészt fordítva mindegyik körrendszer elölről és hátulról számított 3., 5. és 6. körén van, a további 8 körén nincs 3-as metszéspont, tehát a megrajzolt, de 3-as metszéspontot nem tartalmazó körök száma 24.
 

Megjegyzés. Tulajdonképpen elég lett volna vizsgálni az XYZ gömb-háromszög 1/6 részét, miután mindegyik csúcsában megrajzoltuk a szögfelező főkört ‐ amit pl. a Z csúcsban az XOZ és YOZ síkok közti szög felezősíkja metsz ki ‐, és így a gömbháromszöget 6 egybevágó gömbháromszögre osztottuk. Valóban, véve egy olyan, O középpontú K kockát, melynek élei párhuzamosak XX'-vel, YY'-vel, ZZ'-vel, minden olyan szimmetriaművelet, amely K-t önmagába viszi át, ugyanezt teszi 42 körünk együttesével. Márpedig a 4. ábrabeli kockán megjelölt háromszögből ‐ ami a felület 1/48 része ‐ szimmetriákkal az egész kockafelület megkapható.
 

 

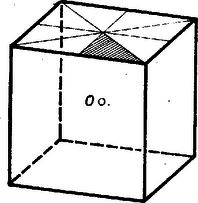4. ábra