Kezdőlap


Feladat:	F.1651	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Beck J. , Csetényi A. , Fialovszky Alice , Frankl P. , Füredi A. , Gegesy F. , Gönczi J. , Kóczy L. , Krasznai A. , Maróti P. , Mozsáry G. , Németh Iván , Prőhle T. , Szalontai Á. , Viszkei Gy.
Füzet:	1969/november, 115 - 117. oldal		PDF \| MathML
Témakör(ök):	Numerikus és grafikus módszerek, Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1969/február: F.1651

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. A leírt szerkesztés körzővel és egyenes vonalzóval elvégezhető, ezért a leírás szerinti 1. ábra bármelyik szakasza és bármelyik szögének bármelyik szögfüggvénye ‐ mint egy legföljebb másodfokú egyenlet gyöke ‐ a négy alapművelettel és négyzetgyökvonással tetszés szerinti pontossággal kiszámítható, miután egy hosszegységet is választottunk. Legyen 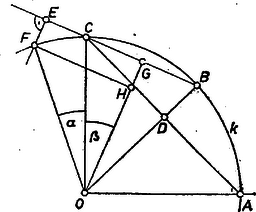$O A = 1$ .

1. ábra

Így a probléma az, hogy táblázatunk

4

tizedes jegyre kerekített, vagyis kerekítési hibával terhelt adatai alapján mekkora hibával kereshetjük vissza a kérdéses szögnek vagy valamely kifejezésének egy (,,pontosan'' ismert) szögfüggvényértékét, továbbá hogy a különböző ilyen visszakeresések közül melyikből kapjuk a kérdéses szöget kisebb hibával. Hibán azt a legnagyobb lehetséges eltérést értjük, ami a szög valódi értéke és a táblázatból lineáris interpoláció útján kapott közelítő értéke között adódhat. (Azzal a kérdéssel már nem foglalkozhatunk tehát, mekkora hibát okoz a lineáris interpoláció elve, hogy ti. pl. a

sin x

függvény grafikonját a táblázat alapján felrajzolt pontok között egyenesszakaszokkal, azaz elsőfokú függvények darabjaival pótoljuk.)

II. Legyen

O

vetülete

B C

-re a

G

pont,

F

vetülete

O G

-re

H

, és a kérdéses szög

C O F ∢ = α

(az állítás szerint közelítőleg

20^{\circ}

). Igen könnyű

sin (α + 22, 5^{\circ})

meghatározása. Ugyanis nyilvánvalóan

B O C ∢ = 45^{\circ}

C O G ∢ = β = 22, 5^{\circ}

, és

\begin{matrix} sin H O F ∢ = sin (α + β) = \frac{H F}{O F} = H F = G E = G C + C E = \\ sin β + D B = sin \frac{45^{\circ}}{2} + (1 - cos 45^{\circ}) = \\ = 1 - \frac{\sqrt[]{2}}{2} + \frac{\sqrt[]{2 - \sqrt[]{2}}}{2} = 0, 675 576 6 ... & (1) \end{matrix}

(\sqrt[]{2}

tizedes alakú közelítő törtjét

10

tizedesre számítottuk ki, ez bőven elegendő (sőt sok is) ahhoz, hogy a második négyzetgyök

8

-ik tizedesjegyét és

sin H O F ∢

fenti

7

tizedesjegyét még biztosan megadhassuk; a számítást nem részletezzük.

)

Mármost a táblázat szerint

sin 42^{\circ} 30' = 0, 6756

, a kerekítés okozta hiba abszolút értéke nem nagyobb, mint

ε = 0, 5 \cdot 10^{- 4}

, így

sin 42^{\circ} 30'

a következő korlátok közé zárható:

\begin{matrix} k_{0} = 0, 675 55 ≦ sin 42^{\circ} 30' ≦ 0, 675 65 = K_{0} . \end{matrix}

sin (α + β)

fent kiszámított értéke két korlát közé esik, eszerint

α + β

nagyobb is, kisebb is lehet, mint

x_{0} = 42^{\circ} 30'

.
A sinus-táblázat szomszédos adatai az

x_{1} = 42^{\circ} 20'

és

x_{2} = 42^{\circ} 40'

helyeken

0, 6734

, ill.

0, 6777

, hibájuk ugyancsak legföljebb

ε

, így alsó és felső korlátjuk,

k_{1}

K_{1}

, ill.

k_{2}

K_{2}

hasonlóan képezhető. Ezek szerint

sin x

-et az

(x_{1}

x_{2})

intervallumban interpoláló két elsőfokú függvény-darab grafikonja abban a két paralelogrammából álló sávban halad, amelyet a 2. ábra vázol (a jobb áttekintés érdekében torzítva). Bárhol van ugyanis a

sin x_{1}

és

sin x_{0}

pontos értékét ábrázoló pont a

k_{1} K_{1}

, ill.

k_{0} K_{0}

szakaszon, az ezeket összekötő szakasz mindenesetre benne van a

k_{1} k_{0} K_{0} K_{1}

négyszögben. (A korlátokat ábrázoló pontokat ‐ a megfelelő abszcisszájú egyenesen ‐ ugyanúgy jelöltük, mint a korlátokat.)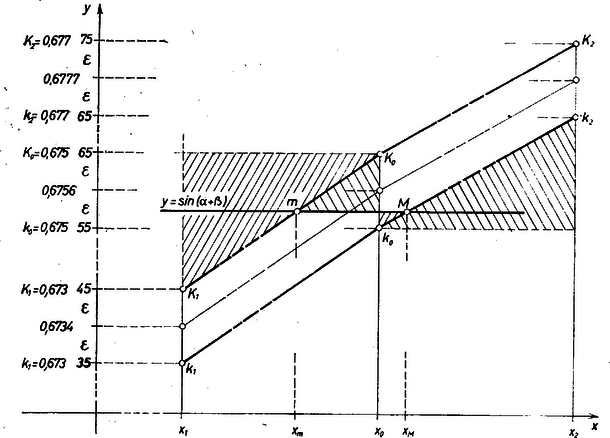

2. ábra

Messe a visszakeresendő értéket ábrázoló

y = sin (α + β)

egyenes a sáv határait az

m

M

pontokban. Ekkor a

sin (α + β)

értéket valamely olyan

x

helyen veszi fel a

sin x

-et interpoláló mondott függvény, mely a grafikon

x

tengelyén az

m M

szakasz vetületére, az

x_{m}

és

x_{M}

abszcisszák közé esik. Így

x_{m}

lesz

α + β

alsó korlátja,

x_{M}

pedig a felső korlátja.
Mármost az

(x_{1}

x_{0})

intervallumban

10'

növekedésre az interpoláló függvény növekedése

0, 0022

és persze ugyanennyi a

K_{0} - K_{1} = k_{0} - k_{1}

növekedés is. Másrészt

K_{0} - sin (α + β) < 0,000 074

, ezért a vonalkázott hasonló háromszögpár alapján

\begin{matrix} x_{0} - x_{m} < 10' \cdot \frac{0, 000 074}{0, 0022} < 21'', \end{matrix}

(2)

és hasonlóan az

(x_{0}

x_{2})

intervallumból

\begin{matrix} x_{M} - x_{0} < 10' \cdot \frac{0, 000 027}{0, 0021} < 8'', \end{matrix}

ennélfogva

42^{\circ} 29' 39'' < α + β < 42^{\circ} 30' 8'',

19^{\circ} 59' 39'' < α < 20^{\circ} 0' 8''

.
Amennyiben egyetlen korláttal akarjuk jellemezni, milyen mértékben közelíti

α

20^{\circ}

-os szöget, akkor eredményünk:

| α - 20^{\circ} | < 21''

Megjegyzések. 1. Könnyű belátni, hogy az

α

-ra számítandó hibakorlát csak attól függ, hogy a visszakeresésben a függvényt ábrázoló görbe milyen meredek szakaszát használjuk. Pl. (1) alapján

cos (α + β)

-t kiszámítva

\begin{matrix} sin α = sin (α + β) cos β - cos (α + β) sin β \end{matrix}

is számítható, ezt a fentihez hasonlóan visszakeresve kisebb hibakorlátot kapnánk, mert

20^{\circ}

környezetében a

sin x

függvény grafikonja meredekebb,

10'

-re eső növekedése

0, 0027

.
Csökkenthetnők a hibakorlátot pl.

tg (α + β)

alapján való hasonló visszakereséssel is. Azonban a visszakeresendő érték ,,pontos'' (a táblázat kerekítésénél jóval kisebb hibájú) meghatározása egyre több számolással járna.
2.

7

tizedes jegyre

sin 42^{\circ} 30' = 0, 675 5902

, tehát hiánnyal közelítjük

42^{\circ} 30'

-et, ebben a környezetben

sin x

-nek

1'

-re eső növekedése

2145 \cdot 10^{- 7}

, és végül

α = 19^{\circ} 59' 56, 2''

.
3. A régebbi,

0, 1^{\circ} = 6'

lépéshosszú iskolai táblázatban a

sin 42^{\circ} 30'

adattól szomszédai,

sin 42^{\circ} 24'

és

sin 42^{\circ} 36'

egyaránt

13 \cdot 10^{- 4}

-nel térnek el, ezekből

x_{0} - x_{m} < 21''

és

x_{M} - x_{0} < 9''

adódik.
4. A fenti második négyzetgyökvonás alapja irracionális szám, azonban tetszés szerinti számú tizedes jegye meghatározható, így ugyanez áll négyzetgyökére is. A kitűzésbeli zárójeles megjegyzés tehát élesíthető volna. Ezzel csak arra kívánta felhívni a szerkesztőség a megoldók figyelmét, hogy

cos 45^{\circ}

és

sin 22, 5^{\circ}

értékét ne a táblázatból vegyék. Ha ezeknek is a kerekített értékét használnók, akkor (1) szerint

0, 6755 < sin (α + β) < 0, 6757

, a 2. ábra egyenese helyére egy

0, 0002

széles sáv lépne, melynek tengelye az

y = 0, 6756

egyenes, és (2)-helyére a következő számítás lépne

\begin{matrix} x_{0} - x_{m} < 10' \cdot \frac{0, 000 15}{0, 0022} < 41'', \end{matrix}

és ugyanennyi lenne

x_{M} - x_{0}

felső korlátja is.