Feladat: F.1649 Korcsoport: 14-15 Nehézségi fok: nehéz
Megoldó(k):  Bajmóczy E. ,  Barbarits A. ,  Beck J. ,  Chikán B. ,  Csetényi A. ,  Donga Gy. ,  Fazekas B. ,  Fazekas G. ,  Fischer Ágnes ,  Frankl P. ,  Füredi A. ,  Gönczi I. ,  Hadik R. ,  Harmat Péter ,  Hermann T. ,  Inczédy Sarolta ,  Kálmán M. ,  Kebely Ágnes ,  Kemény A. ,  Kérchy L. ,  Kirschner I. ,  Kóczy L. ,  Komjáth P. ,  László I. ,  Lázár A. ,  Lukács P. ,  Magyar Á. ,  Martoni V. ,  Molnár Gy. ,  Németh Iván ,  Nikodémusz Anna ,  Papp Z. ,  Prőhle T. ,  Reviczky J. ,  Schván P. ,  Somorjai G. ,  Szalontai Á. ,  Terjéki J. ,  Várhegyi Éva ,  Walthier T. ,  Waszlavik L. 
Füzet: 1969/szeptember, 15 - 17. oldal  PDF  |  MathML 
Témakör(ök): Irracionális számok és tulajdonságaik, Síkgeometriai számítások trigonometria nélkül sokszögekben, Szimmetrikus sokszögek, Ellenpélda, mint megoldási módszer a matematikában, Feladat
Hivatkozás(ok):Feladatok: 1969/február: F.1649

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) Legyen egy a feltevéseket teljesítő nyolcszög ABCDEFGH=N, vagyis mindegyik szöge 135∘. Az AB, CD egyenesek metszéspontját P-vel jelölve BCP egyenlő szárú derékszögű háromszög, mert B-nél és C-nél levő szöge, mint N-nek külső szöge, 45∘, így a BPC∢ derékszög, CD⊥AB. Ugyanígy CD⊥EF⊥GH, ez a négy egyenes egy PQRS téglalapot határol (1. ábra).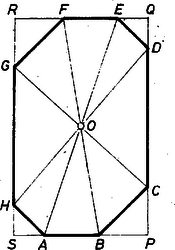

 

 

1. ábra
 

Ezek alapján
SP=SA+AB+BP=HA2+AB+BC2,RQ=RF+FE+EQ=GF2+FE+ED2,


és ezek egyenlőségéből, kellő rendezéssel
AB-FE=12(GF+ED-HA-BC).

Itt a bal oldal egész szám, és egész a jobb oldali zárójel értéke is. Ez csak úgy lehetséges, ha mindkét oldal 0. Ha ugyanis egyik nem az, akkor a másik sem, így pedig 2 egyenlő volna a zárójeles kifejezés és a bal oldal hányadosával, ami racionális szám, holott 2 irracionális szám.
Eszerint AB=FE, s mivel még párhuzamosak is, ABEF paralelogramma, azért átlói, AE és BF felezik egymást az O metszéspontjukban, más szóval az A, E, valamint B, F csúcs-párok egymás tükörképei O-ra nézve.
Ugyanígy BC♯FG, ezért BF felezőpontja ‐ az O pont ‐ felezi CG-t is, másrészt AH♯ED alapján O ‐ mint AE felezőpontja ‐ a DH átlót is felezi, tehát N kerületének EFGHA és ABCDE részei egymás tükörképei O-ra nézve. Ezt kellett bizonyítanunk.
b) Példát mutatunk egész oldalú, egyenlő szögű és centrálisan nem szimmetrikus hatszögre és 12-szögre, ezek mutatják, hogy a nyolcszögre vonatkozó állítás megfelelője hatszögre és 12-szögre nem érvényes.
Messe egymást a 2 egységnyi oldalú ABCDEF szabályos hatszög FA és CB oldalegyenese P-ben, és legyen az ABP szabályos háromszög AB-vel párhuzamos és egyirányú középvonala A1B1 (2. 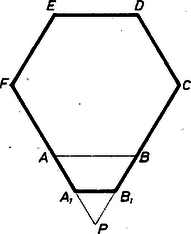ábra).
 

 

2. ábra
 

Ekkor az A1B1CDEF hatszög mindegyik szöge 120∘, és egymás utáni oldalainak hossza rendre 1, 3, 2, 2, 2, 3, a szemben fekvő oldalpárok különbözők, az idom nem centrálszimmetrikus.
Legyen másrészt a 2 egységnyi oldalú szabályos 12-szög 5 egymás utáni oldalából álló törött vonal ABCDEF (3. ábra), a CD oldal fölé kifelé írt szabályos háromszögnek CD-vel párhuzamos és egyirányú középvonala C1D1, a C1CB és a D1DE háromszöget ebben a körüljárásban paralelogrammává kiegészítő pont 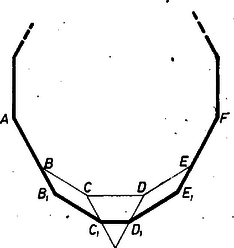B1, ill. E1.
 

 

3. ábra
 

Könnyű belátni, hogy ez rajta van az AB, ill. FE oldal meghosszabbításán, így a 12-szög kerületének mondott részét AB1C1D1E1F-fel pótolva megfelelő ellenpéldát adtunk: a szögek egyenlők a megfelelő eredeti oldalak szögével, tehát egymással is, az oldalak hosszai 3, 2, 1, 2, 3, és nyilvánvalóan nem áll fenn centrális szimmetria.
 

Harmat Péter (Mosonmagyaróvár, Kossuth L. Gimn., III. o. t. )