Kezdőlap


Feladat:	F.1647	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1969/október, 54 - 56. oldal		PDF \| MathML
Témakör(ök):	Egészrész, törtrész függvények, Feladat
Hivatkozás(ok):	Feladatok: 1969/február: F.1647

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Ábrázoljuk először (1) első tagját. Az $\frac{x}{3}$ függvény képe az $x$ függvény képéből $x$ tengely menti 3-szoros nyújtással áll elő, hiszen amely értéket az utóbbi az $a$ helyen felvesz, azt az előbbi a $3 a$ helyen veszi fel. Ugyanilyen nyújtással áll elő $[\frac{x}{3}]$ képe $[x]$ ismert képéből: lépcsőinek hossza 3-szor akkora, mint a magasságuk; más szóval: a függvény a 3-mal osztható egész helyeken ugrik 1-et fölfelé ( $1_{1}$ ábra).

1. ábra

A 3-mal való szorzás a függvény képében 3-szoros nyújtást jelent az

y

tengely irányában, így

3 [\frac{x}{3}]

képe az

[x]

képéből mindkét irányú, vagyis origó centrumú 3-szoros nagyítással áll elő. Ennélfogva ugyanez a transzformáció állítja elő az

x - 3 [\frac{x}{3}]

függvény képét az

x - [x]

függvény (az ún. törtrész-függvény, fűrész-függvény) ismert képéből, hiszen az

x

függvényt a középpontos nagyítás önmagába viszi át (

1_{2}

ábra). Ez a függvény periodikus, periódusa 3.
Végül ebből

[x - 3 [\frac{x}{3}]]

ugyancsak 3 periódusú függvény (

1_{3}

ábra); mondhatjuk: az

[x] : 3

osztás maradékát adja meg (az egész számok osztásánál szokásos értelemben), így

x

növekedésével egész számra rálépve két egymás utáni esetben

1

-et

- 1

-et nő, a következő ilyen esetben, 3-mal osztható egész értékre rálépve,

2

-t csökken.
Ugyanezek állnak (1) második tagjára, így a bal oldal

x

és

y

szerint egyaránt periodikus, periódusa 3, továbbá értéke az egész abszcisszájú és ordinátájú rácsegyenesekkel egységnégyzetekre felosztott sík minden kis négyzetében állandó, éspedig annyi, mint bal alsó csúcsában. A (0; 0), (3; 0), (3; 3) és (0; 3) csúcsokkal meghatározott négyzet 9 egységnégyzetében felvett értékeket a 2. ábra tünteti fel, ezek alapján a követelménynek megfelelő pontok halmazát az előírt

a

értékekre a

3_{1}

3_{2}

ábrák vázolják vonalkázással. A jelölt egységnégyzetekhez alsó és bal oldaluk hozzáértendő, ezeknek jobb, ill. felső végpontja nélkül.

2. ábra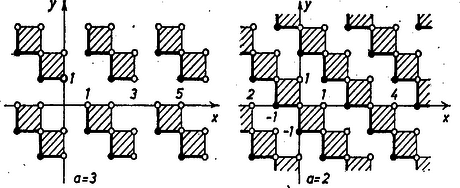

3. ábra

II. megoldás. Az egész-rész-függvényt meghatározó (2) egyenlőtlenségrendszerben

x

helyére

x / 3

-at írva és 3-mal szorozva

\begin{matrix} 3 [\frac{x}{3}] \leq x < 3 [\frac{x}{3}] + 3, azaz 0 \leq x - 3 [\frac{x}{3}] < 3, \end{matrix}

s így (1) bal oldalának mindegyik tagja csak a

0, 1, 2

értékeket veheti fel.

a = 3

mellett tehát csak úgy teljesülhet az egyenlet, ha a bal oldal egyik tagja 1, a másik 2;

a = 2

esetében pedig úgy, hogy vagy mind a két tag 1, vagy az egyik 0, a másik 2.
Vizsgáljuk meg, hogy milyen

z

értékekre teljesül

\begin{matrix} [z - 3 [\frac{z}{3}]] = b, \end{matrix}

ahol

b = 0

1

vagy

2

. Ez, ismét (2) szerint azt jelenti, hogy

\begin{matrix} b \leq z - 3 [\frac{z}{3}] < b + 1, \end{matrix}

tehát a

z

szám

3 k + r

alakú, ahol

k

egész és

b \leq b + 1

.
Ezek szerint (1)

a = 3

mellett azokra a pontokra teljesül, amelyeknek koordinátái

x = 3 m + u

y = 3 n + v

alakúak, ahol

m

n

egész és

\begin{matrix} 1 \leq u < 2 és 2 \leq v < 3, vagy 2 \leq u < 3 és 1 ≦ v < 2; \end{matrix}

a = 2

esetén pedig az ugyanilyen alakú koordinátákkal jellemzett pontokra, ahol azonban most

\begin{matrix} 0 \leq u < 1 és 2 \leq v < 3 vagy 1 \leq u, v < 2 vagy 2 \leq u < 3 és 0 \leq v < 1. \end{matrix}

Ezeket a pontokat a

3_{1}

3_{2}

ábrák bevonalkázott négyzetei ábrázolják, nem számítva hozzájuk felső és jobb oldali határukat.