Kezdőlap


Feladat:	F.1646	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Ágoston P. , Baintner L. , Bajmóczy E. , Beck J. , Donga Gy. , Fialovszky Alice , Fischer Á. , Győry Gy. , Hadik R. , Horváth L. , Kemény A. , Kóczy L. , László I. , Lázár A. , Lukács P. , Maróti Péter , Martoni V. , Mihálffy P. , Mozsáry G. , Nagy D. , Papp Z. , Prőhle T. , Schván P. , Somorjai G. , Tarsó B. , Terjéki J. , Várhegyi Éva
Füzet:	1970/november, 109 - 113. oldal		PDF \| MathML
Témakör(ök):	Ábrázoló geometria, Háromszögek hasonlósága, Tengely körüli forgatás, Trigonometriai azonosságok, Síkgeometriai számítások trigonometria nélkül háromszögekben, Tetraéderek, Szögfüggvények a térben, Feladat
Hivatkozás(ok):	Feladatok: 1969/január: F.1646

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen egy, az előírásoknak megfelelő gúla $A B C D$ úgy, hogy az $A B C$ alaplapon $B C = C A = 1$ , $A B = c$ , és ezekhez igazodva az oldalélek $D A = 1$ , $D B = D C = c$ (az 1. ábrán távlati rajzban, a 2. ábrán két vetületben úgy, hogy a II. képsík merőleges $A C$ -re; $D'$ -t az $A C D$ , $B C D$ lapok leforgatott $A C D^{*}$ , $B C (D)$ helyzetéből szerkesztettük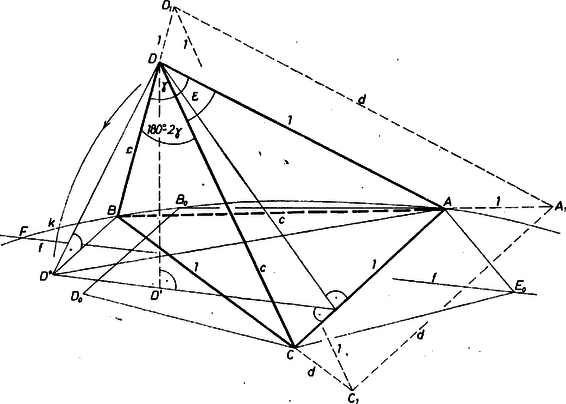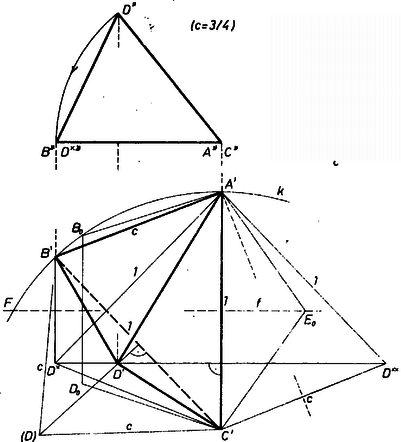: $D^{*} D' ⊥ A' C'$ és $(D) D' ⊥ B' C')$ .

1. ábra

2. ábra

Az 1. ábrán jól látjuk, hogy az egyenlő hosszú élek hármasával egymás után csatlakoznak és nyitott törött vonalat alkotnak, az egységnyiek

B C A D

-t, a

c

hosszúságúak

A B D C

-t. Mind a négy lapháromszög egyenlő szárú és páronként egybevágók,

A D C

-ben és

C B A

-ban a szárak hossza

1

, az alapé

c

, ezért

c < 2

B D A

-ban és

D B C

-ben a két szár

c

, az alap

1

, ezért

c > - 1 / 2

(a lapok leírásában a testre kívülről ránézve pozitív körüljárás szerint haladtunk).
Csak azokat a gúlákat tekintjük, amelyekben

c \leq 1

, mert minden ilyet

1 / c = d

-szeresére nagyítva (

d \geq 1

) ismét a vizsgált osztályba tartozó gúlát kapunk,

3 - 3

db egységnyi, ill.

d

hosszúságú éllel, és

6

élének kölcsönös helyzete is az előírás szerinti. Valóban, a nagyítás középpontjának

B

-t véve

B A_{1} = B D_{1} = 1

B C_{1} = d

, rendre

D_{1}

A_{1}

B

C_{1}

felel meg

A

B

C

D

-nek (tükörkép !), és a fenti két jellemző törött vonal

A_{1} B D_{1} C_{1}

-ben (

1

-élek), ill.

D_{1} A_{1} C_{1} B

-ben (

d

-élek) adódik. Eszerint

c

keresett alsó korlátjának reciproka megadja

d

felső korlátját.
Forgassuk bele az

A C D

háromszöget

A C

oldala körül az

A B C

háromszög síkjába úgy, hogy

D

új helyzetében

A C

-nek ugyanazon az oldalán legyen, mint

B

, és jelöljük ezt az új helyzetet

D^{*}

-gal. Az

A C D^{*}

A C B

háromszögek egybevágók, mert megfelelő oldalaik egyenlők (

A D^{*}

-nak

B C

felel meg). Mivel

A C

oldaluk közös, e két háromszög szimmetrikusan helyezkedik el az

A C

oldal

f

felező merőlegesére nézve, és

B D^{*} ∥ A C

. Forgatás közben a

D

pont az

A C

-re merőleges síkban mozog, így

D D^{*}

merőleges az

A C

-vel párhuzamos

B D^{*}

-ra, vagyis a

B D^{*} D

háromszögben

D^{*}

-nál derékszög van, ezért

c = B D > B D^{*}

.
Helyezzünk az

A C

szakaszra egy

A E_{0} C D_{0} B_{0}

szabályos ötszöget ‐ melynek tehát

A C

átlója ‐ úgy, hogy

B_{0}

A C

egyenesnek ugyanazon az oldalán legyen, mint

B

. A

B

B_{0}

pontok a

C

körüli, egységnyi sugarú

k

körön vannak, pontosabban annak kisebbik

A F

ívén, ahol

F

k

és

f

metszéspontja. Megmutatjuk, hogy

B

B_{0} F

íven van.
Láttuk, hogy

B

-nek

f

-től mért távolsága, a

B D^{*}

szakasz fele kisebb, mint az

A

-tól mért távolságának a fele.

B_{0}

-nak

f

-től mért távolsága viszont éppen feleakkora, mint az

A

-tól mért távolsága, és a

k

kör

B_{0} A

ívének pontjai

f

-től távolabb vannak, mint

B_{0}

A

-hoz viszont

B_{0}

-nál közelebb vannak.

B

tehát nem lehet a

B_{0} A

íven. Emiatt

A B > A B_{0}

, vagyis

\begin{matrix} c > c_{0}, \end{matrix}

ahol

c_{0}

az egységnyi átlójú szabályos ötszög oldala.

c_{0}

értéke a következő módon határozható meg. Legyen a

C B_{0}

A D_{0}

átlók metszéspontja

G

(3. ábra,

B

mellé

0

index teendő).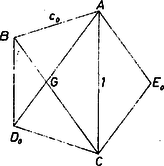

3. ábra

A C B_{0}

B_{0} G A

háromszögek hasonlósága alapján

G B_{0} : B_{0} A = B_{0} A : A C

, azaz

\begin{matrix} (1 - c_{0}) : c_{0} = c_{0} : 1, \\ c_{0}^{2} + c_{0} - 1 = 0, \\ c_{0} = \frac{\sqrt[]{5} - 1}{2} \end{matrix}

(hiszen az egyenlet másik gyöke negatív).
Ezek szerint a

c \leq 1

esetben a vizsgált gúla létezésének szükséges feltétele

\begin{matrix} 1 \geq c > c_{0} = \frac{\sqrt[]{5} - 1}{2} (= 0, 618) . \end{matrix}

(1)

Megmutatjuk, hogy ez a feltétel elégséges is. Ha ugyanis

c

egy tetszőleges valós szám, amelyre (1) teljesül, legyen az

A B C

háromszögben

A C = C B = 1

A B = c

(

c_{0} > 1 / 2

miatt (1)-ből következik, hogy ilyen háromszög létezik), és legyen

D^{*}

B

tükörképe az

A C

szakasz

f

felező merőlegesére nézve. Tükrözzük

D^{*}

-ot az

A C

egyenesre, kapjuk

D^{* *}

-ot. Az

A D^{* *} C

háromszög is egyenlő szárú (

A C = A D^{* *} = 1

), ezért

C D^{* *}

felező merőlegese átmegy

A

-n. Ennek a felező merőlegesnek

B

ugyanazon az oldalán van, mint

C

, tehát

B C < B D^{* *}

, és mivel

B C \geq c

, azért

B D^{* *} > c

. Ha tehát a

D^{*}

pontot

A C

körül a

D^{* *}

helyzetbe forgatjuk át, a

B

-től mért távolsága valamelyik közbülső helyzetben

c

-vel lesz egyenlő. Jelöljük ezt a közbülső helyzetet

D

-vel, ekkor

A B C D

a kívánt tulajdonságú tetraéder, hiszen

A C = B C = A D = 1

, és

A B = B D = D C = c

.
A 2. bekezdés végén mondottak alapján a kérdéses gúla létezésének szükséges és elégséges feltétele most már:

\begin{matrix} \frac{\sqrt[]{5} - 1}{2} = c_{0} < c < {\frac{1}{c}}_{0} = \frac{\sqrt[]{5} + 1}{2} . \end{matrix}

(2)

II. megoldás. A fenti jelöléseket használva továbbra is a

c \leq 1

esetet tekintjük. Legyen a szárral szemben fekvő szög az egységnyi szárú lapháromszögben

ε

, a

c

szárúban

γ

, így

c \leq 1

alapján

ε \geq 60^{\circ}

γ \leq 60^{\circ}

és

180^{\circ} - 2 γ \geq 60^{\circ}

, így

D

-ben a három él közti szögek legkisebbike a

B D A ∢

(4. és 1. ábra).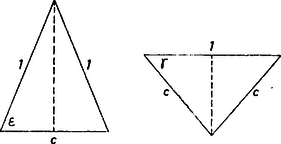

4. ábra

Felhasználjuk, hogy triéder két oldalának (más szóval élszögének) összege nagyobb a harmadiknál. Eszerint a

D

csúcsú triéderben fennáll

\begin{matrix} B D A ∢ + C D A ∢ & > B D C ∢, \\ γ + ε & > 180^{\circ} - 2 γ, \\ ε & > 180^{\circ} - 3 γ ≧ 0^{\circ}, \end{matrix}

és mivel a cosinusfüggvény a (

0

90^{\circ}

) intervallumban monoton csökken:

\begin{matrix} cos ε < cos (180^{\circ} - 3 γ) = - cos 3 γ = 3 cos γ - 4 cos^{3} γ, \\ \frac{c}{2} < \frac{3}{2 c} - \frac{1}{2 c^{3}} . \end{matrix}

Innen

c > 0

alapján

\begin{matrix} c^{4} - 3 c^{2} + 1 = {(c^{2} - \frac{3}{2})}^{2} - \frac{5}{4} = (c^{2} - \frac{3}{2} - \frac{\sqrt[]{5}}{2}) (c^{2} - \frac{3}{2} + \frac{\sqrt[]{5}}{2}) < 0, \end{matrix}

a tényezők ellentett előjelűek, és

c^{2} \leq 1

alapján az első negatív, tehát a második pozitív, és ebből

\begin{matrix} c^{2} > \frac{3 - \sqrt[]{5}}{2} = \frac{6 - 2 \sqrt[]{5}}{4} = {(\frac{\sqrt[]{5} - 1}{2})}^{2}, c > \frac{\sqrt[]{5} - 1}{2} . \end{matrix}

Tovább az I. megoldás szerint haladhatunk.

Megjegyzés. A felhasznált segédtétel bizonyításában elég a legnagyobb oldalról belátni, hogy kisebb a másik kettő összegénél.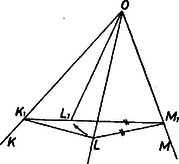

5. ábra

Legyen

K O M ∢ \geq L O M ∢

(5. ábra), vágjuk fel az

O L

élt és forgassuk rá az

L O M

lapot

O M

körül

K O M

-re, legyen

L

új helyzete (a

K O M

szögtartományban, vagy az

O K

félegyenesen)

L_{1}

. Messe egy, az

L_{1}

-en átmenő egyenes

O M

-et

M_{1}

-ben,

O K

-t

K_{1}

-ben. Így

\begin{matrix} K_{1} L + L M_{1} > K_{1} M_{1}, L K_{1} > K_{1} M_{1} - L_{1} M_{1} = K_{1} L_{1}, \end{matrix}

hiszen

L_{1} M_{1} = L M_{1}

. Mivel végül az

O K_{1} L

és

O K_{1} L_{1}

háromszögek

O

-ből induló oldalai páronként egyenlők, azért

\begin{matrix} K_{1} O L ∢ > K_{1} O L_{1} ∢ = K O M ∢ - L O M ∢, \end{matrix}

ami egyértelmű állításunkkal.
(Ha

L_{1}

O K_{1}

élre esik, állításunk nyilvánvaló.)