Feladat: F.1645 Korcsoport: 14-15 Nehézségi fok: átlagos
Megoldó(k):  Beck J. ,  Füredi András ,  Somorjai G. ,  Viszkei Gy. 
Füzet: 1970/november, 107 - 109. oldal  PDF  |  MathML 
Témakör(ök): Egyenesek egyenlete, Hiperbola egyenlete, Projektív geometria, Hiperbola, mint kúpszelet, Hiperbola, mint mértani hely, Feladat
Hivatkozás(ok):Feladatok: 1969/január: F.1645

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az ABC háromszögről feltesszük, hogy CA≠CB, hiszen a CA=CB eset gyorsan áttekinthető és érdektelen eredményt nyújt: a metszéspontot Cx-szel jelölve (hiszen maga C a kiindulási helyzetbeli metszéspont), ez nyilvánvalóan mindig a háromszög szimmetriatengelyén van; és a tengely minden Cx pontja hozzátartozik a mértani helyhez, mert a CxAC és CxBC szög egymás képe a tengelyre, így nagyságuk egyenlő és forgási irányuk ellentétes. Csak az AB alap felezőpontja nem tartozik hozzá a mértani helyhez, mert amikor a forgás közben AC az AB-re jut, ugyanakkor BC a BA-ra, így minden pontjuk közös, nincs egyértelmű metszéspont.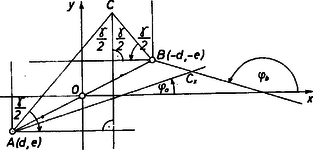
Legyen az AC egyenes forgási iránya az, amelyben az AC félegyenest π-nél kisebb elfordulás viszi át AB-be (1. ábra).

 
 
1. ábra
 

Amely pillanatban mindkét egyenes megtett elfordulása az ACB szög felének pótszöge, akkor mindkettő merőlegesen áll ennek a szögnek a felezőjére (és CA≠CB miatt azt különböző pontokban metszik), tehát párhuzamosak, metszéspont nem jön létre. Nincs metszéspont a további 90∘-os elfordulás helyzetében sem.
Vezessünk be koordináta-rendszert, válasszuk ennek y tengelyét az ACB szög belső szögfelezőjével párhuzamosnak, origója legyen az AB oldal felezőpontja, és legyenek A koordinátái (d, e), így B koordinátái (-d, -e), ahol d≠0, különben a szögfelező nem választhatná szét A-t és B-t, továbbá e≠0, mert háromszögünk nem egyenlő szárú.
Az indulási helyzetben AC irányszöge π-γ2 (az abszcisszatengelyhez viszonyítva), BC-é π+γ2, így a szögsebesség közös abszolút értékét egységnyinek véve, t idő múlva az irányszögek
φa=π-γ2-tésφb=π+γ2+t,
vagyis a mozgás bármely pillanatában φa+φb=π. Ezért iránytangenseikre ma+mb=0, a φa=φb=π/2 érték kivételével. A kivett esetet már elintéztük, úgyszintén a φa=0 esetet is. Minden más esetben a két egyenes egyenlete
y-e=ma(x-d),
illetőleg
y+e=mb(x+d)=-ma(x+d),
így Cx metszéspontjuk koordinátái ma-val kifejezve
xc=-ema,yc=-madmivel márma≠0).

Innen az ma paraméter kiküszöbölésével a két koordináta összefüggése
xcyc=de(≠0).(1)
Ez hiperbola egyenlete, melynek középpontja AB felezőpontja, aszimptotái párhuzamosak a C-nél levő belső és külső szög felező egyeneseivel.
Maga az A és B pont is rajta van a hiperbolán, hiszen koordinátáik kielégítik (1)-et, másrészt a mértani helyhez is hozzátartoznak, hiszen egy helyzetben AC átmegy B-n, és egy másikban BC átmegy A-n.
A hiperbola minden, az A-tól és B-től különböző Cx pontja is hozzátartozik a mértani helyhez, ugyanis a CxA egyenes iránytangense
yc-exc-d=dexc-exc-d=-exc,
(x≠0, mert a hiperbolának nincs pontja az y-tengelyen és Cx≠A miatt xc-d≠0), ill. hasonlóan a CxB iránytangense
yc+exc+d=exc,
összegük 0, ezért a két egyenes irányszöge π-re egészíti ki egymást, tehát ez a helyzet a forgás közben előáll.
Ezek szerint a mértani hely (CA≠CB esetén) a mondott hiperbola.
 

Megjegyzések. 1. Elemi úton is megkapható, hogy ‐ felvéve az AB oldal O felezőpontján át az f-fel párhuzamos f' és a rá merőleges f'' egyenest ‐ Cx-nek ezektől mért távolságai fordítva arányosak egymással, ez pedig hiperbolát jelent (2. ábra, csak a γ/2 pótszögénél kisebb elfordulási szögekre szorítkozva).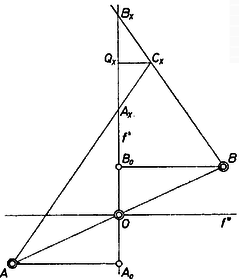
 
 
2. ábra
 

Messe f'-t ACx az Ax, BCx a Bx pontban, és legyen A, B, Cx vetülete f-en rendre A0, B0, Qx. Ekkor nyilvánvalóan
AA0=BB0,A0Ax=B0Bx,AxBx=A0B0,QxBx=OB0,B0Bx=OQx,
és a CxBxQx és BBxB0 háromszögek hasonlóságából
QxCxQxBx=QxCxOB0=B0BB0Bx=B0BOQx,CxQx=(BB0⋅OB0)⋅1OQx,


ahol a zárójelbeli szorzat állandó.
2. Ugyancsak elemi a következő bizonyítás is (de ebben sem tekintünk nagyobb elfordulásokat, sem a szakaszok előjelét). Messe az ABCx), háromszög ACx-szel párhuzamos OD középvonala az ACxB szög felezőjét R-ben (3. ábr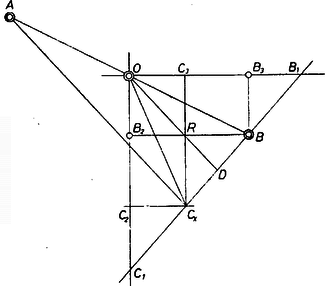a).
 
 
3. ábra
 

Ekkor DR=DCx=DB, így Thalész tétele alapján RB⊥CxR.
Messe továbbá BCx, az O-n át RCx szel és RB-vel párhuzamosan húzott egyeneseket C1 ben, ill. B1-ben, és legyen Cx vetülete ezeken C2, C3, a B-é pedig B2, B3. Ekkor D a B1C1-et is felezi, így B1B=C1Cx, ezért a B1BO és C1CxO háromszögek területe egyenlő, ugyanez áll a B1BB3 és CxC1C2 háromszögekre is, hiszen egybevágók, tehát ezeket elvéve OB3B és OCxC2 háromszögek területe egyenlő és ennélfogva az OB3BB2, OC3CxC2 téglalapok területe is egyenlő: OC3⋅OC2=állandó.
Lényegében azt a tulajdonságát használtuk itt fel a hiperbolának, hogy bármely szelőjének felezőpontjára nézve az aszimptotákkal való metszéspontok (ugyancsak) egymás tükörképei.
3. Megoldható a feladat projektív geometriai ismeretek fölhasználásával is, lásd az ezen számunk 97. oldalán olvasható cikket.