Kezdőlap


Feladat:	F.1643	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bajmóczy E. , Balogh Z. , Barbarits A. , Beck J. , Csetényi A. , Czibolya L. , Eller J. , Fazekas G. , Fialovszky Alice , Frankl P. , Galántai A. , Gegesy F. , Gerhardt T. , Hadik R. , Kálmán M. , Karvaly G. , Kóczy L. , Komjáth P. , László I. , Maróti P. , Müller Zója , Nagy D. , Papp Zoltán , Sailer K. , Somorjai G. , Szabó P. , Szőnyi Á. , Terjéki J. , Viszeki Gy. , Walthier T. , Zambó Péter
Füzet:	1970/január, 6 - 9. oldal		PDF \| MathML
Témakör(ök):	Számelrendezések, Fizikai jellegű feladatok, Számtani sorozat, Síkidomok súlypontja, Feladat
Hivatkozás(ok):	Feladatok: 1969/január: F.1643

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Síkbeli pontrendszer súlypontja (tömegközéppontja) ‐ mint a fizikából ismeretes ‐ az a pont, amelybe a rendszer össztömegével egyenlő (szokásos jelöléssel $\sum m$ ) tömeget gondolva, ennek bármely (forgási) tengelyre számított nyomatéka egyenlő a rendszer egyes tömegei nyomatékának összegével. A nyomatékot a tömeg és a tengelytől mért (előjellel együtt értett) távolság (kar) szorzata adja. A tömegközéppont helyzetét két különböző irányú tengelytől mért távolságával határozhatjuk meg (a tengelyeket természetesen a síkban véve). A koordinátatengelyeket úgy célszerű választani, hogy minden mező középpontjának a távolsága a legközelebbi pont távolságának többszöröse legyen.

I. Helyezzük a sakktáblát a szokásos derékszögű koordinátarendszerbe és válasszuk ennek hosszúságegységét úgy, hogy az

1

. sor és

1

. oszlop közös mezeje középpontjának koordinátái

(1,1)

legyenek, a

2

. sor és

2

. oszlop közös mezeje középpontjáé pedig

(2,2)

. Ekkor ‐ a sakkban szokásosan alulról fölfelé számozott ‐

i

-edik sor és balról jobbfelé

j

-edik oszlop közös mezeje középpontjának koordinátái nyilvánvalóan

(j, i)

, az ide tett anyagi pont tömege az első tömegpontrendszer esetében

j + i - 1

. Így minden egyes anyagi pontnak az

x

y

tengelyre vonatkoztatott karját megadja az ordinátája, ill. abszcisszája, másrészt a pontrendszer nyilvánvaló szimmetriája miatt a

T

tömegközéppont két koordinátája egyenlő, elég

x_{T}

abszcisszáját meghatároznunk.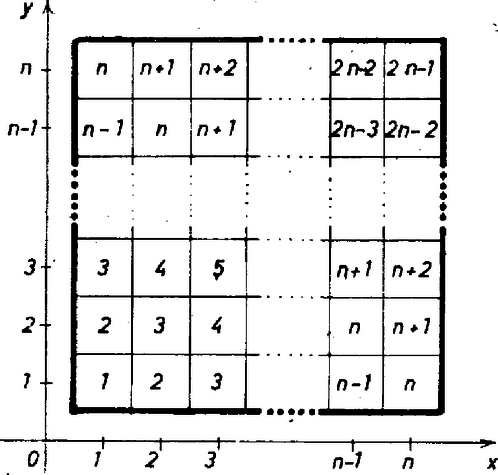

1. ábra

A tömegek összege céljára tekintsük az egyes oszlopokbeli tömegek összegét. Mértékszámaik minden oszlopban fölfelé növekvő,

1

differenciájú számtani sorozatot alkotnak. Az első oszlopban

\begin{matrix} s_{1} = 1 + 2 + ... + n = \frac{n}{2} (1 + n) . \end{matrix}

A 2. oszlop tagjai rendre az 1-gyel nagyobb számok, hiszen a

(j, i)

középpontú mező száma

j + (i - 1)

alakban írható, tehát

s_{2} = s_{1} + n

, ugyanígy

s_{3} = s_{2} + n = s_{1} + 2 n, ...

, az oszlopösszegek szintén számtani sorozatot alkotnak. Az utolsó oszlop összege

\begin{matrix} s_{n} = n + (n + 1) + ... + (2 n - 1) = \frac{n}{2} (3 n - 1) \end{matrix}

vagy kellő alakítással:

\begin{matrix} s_{n} = \frac{n}{2} {(1 + n) + 2 (n - 1)} = s_{1} + (n - 1) n, \end{matrix}

így tehát, mint az

n

összeg összege

\begin{matrix} \sum m = \frac{n}{2} {\frac{n}{2} (1 + n) + \frac{n}{2} (3 n - 1)} = \frac{n^{2}}{4} \cdot 4 n = n^{3} . \end{matrix}

A pontrendszernek az

y

tengelyre vett nyomatékában minden egyes oszlop tömegeinek karja (abszcisszája) közös és egyenlő az oszlop sorszámával, így a fentiek alapján

\begin{matrix} \sum m_{k} x_{k} = s_{1} \cdot 1 + s_{2} \cdot 2 + s_{3} \cdot 3 + ... + s_{n} \cdot n = \end{matrix}

\begin{matrix} = (s_{1} + 0 \cdot n) \cdot 1 + (s_{1} + 1 \cdot n) \cdot 2 + (s_{1} + 2 \cdot n) \cdot 3 + ... + {s_{1} + (n - 1) n} \cdot n = \end{matrix}

\begin{matrix} = s_{1} (1 + 2 + 3 + ... + n) + n {(0 \cdot 1 + 1 \cdot 2 + 2 \cdot 3 + ... + (n - 1) n)} . \end{matrix}

(Ebben ‐ a fizikában szokásos ‐ jelölésben a

k

sorszám valamilyen sorrendben végigfut a sakktábla mezőin.)
A második zárójelbeli kifejezés így alakítható

\begin{matrix} (1^{2} - 1) + (2^{2} - 2) + (3^{2} - 3) + ... + (n^{2} - n) = \end{matrix}

\begin{matrix} = (1^{2} + 2^{2} + ... + n^{2}) - (1 + 2 + ... + n) = \end{matrix}

\begin{matrix} = \frac{n (n + 1) (2 n + 1)}{6} - \frac{n (n + 1)}{2} = \frac{n (n + 1)}{6} (2 n - 2) = \frac{(n + 1) n (n - 1)}{3}, \end{matrix}

így

\begin{matrix} \sum m_{k} x_{k} = \frac{n^{2} {(n + 1)}^{2}}{4} + \frac{n^{2} (n + 1) (n - 1)}{3} = \frac{n^{2} (n + 1)}{12} (7 n - 1) . \end{matrix}

Ezzel az

x_{T}

-re vonatkozó egyenlet és megoldása

\begin{matrix} x_{T} \cdot \sum m = \sum m_{k} x_{k}, x_{T} = y_{T} = \frac{\sum m_{k} x_{k}}{\sum m} = \frac{(n + 1) (7 n - 1)}{12 n} . \end{matrix}

(A tömegközéppont semmilyen

n (> 1)

esetén sem esik a tábla egy mezejének középpontjába, mert

x_{T}

nem lehet egész, hiszen

n

n + 1

-hez is,

7 n - 1

-hez is relatív prím.)

II. A második pontrendszer esetében hasonlóan járunk el. Az első oszlopban álló tömegek összege változatlanul

s_{1}

, a 2. oszlopbelieké

2 s_{1}

, hiszen tagról tagra az 1. oszlopbeli szám 2-szeresét írtuk be, hasonlóan a

3., ..., n

-edik oszlop tömeg-összege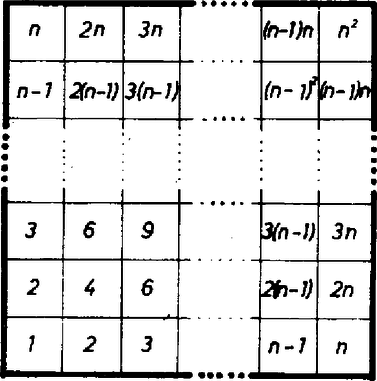

3 s_{1}, ..., n s_{1}

, tehát

\begin{matrix} \sum m = s_{1} + 2 s_{1} + 3 s_{1} + ... + n s_{1} = \end{matrix}

\begin{matrix} = s_{1} (1 + 2 + ... + n) = s_{1}^{2} = \frac{n^{2} {(n + 1)}^{2}}{4} . \end{matrix}

2. ábra

Oszloponként ismét közös az

y

-tengelytől mért távolság, így

\begin{matrix} \sum m_{k} x_{k} = s_{1} \cdot 1 + (2 s_{1}) \cdot 2 + (3 s_{1}) \cdot 3 + ... + (n s_{1}) \cdot n = \end{matrix}

\begin{matrix} = s_{1} (1^{2} + 2^{2} + ... + n^{2}) = \frac{n^{2} {(n + 1)}^{2} (2 n + 1)}{12}, \end{matrix}

és ezek alapján az

U

tömegközéppont koordinátái:

\begin{matrix} x_{U} = y_{U} = \frac{\sum m_{k} x_{k}}{\sum m} = \frac{2 n + 1}{3} . \end{matrix}

Papp Zoltán (Debrecen, Fazekas M. Gimn., IV. o. t.)

Megjegyzések. 1. Első látásra kézenfekvőbb a sakktábla bal alsó sarkát választani a koordinátarendszer origójává. Úgy bonyolultabb számítás eredményeként nyilvánvalóan

1 / 2

-del kisebbnek kaptuk volna a koordinátákat:

\begin{matrix} x'_{T} = y'_{T} = x_{T} - \frac{1}{2} = \frac{7 n^{2} - 1}{12 n}, x'_{U} = y'_{U} = \frac{4 n - 1}{6} . \end{matrix}

Papp Zoltán

2. A

\sum m

összeg egyszerűen képezhető az átlók bármelyikével párhuzamosan való csoportosítással is.