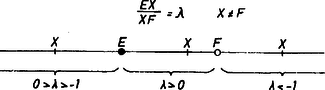Kezdőlap


Feladat:	F.1637	Korcsoport: 14-15	Nehézségi fok: nehéz
Megoldó(k):	Bajmóczy Ervin , Barbarits András , Beck József , Chikán Bálint , Csetényi Artúr , Czibolya L. , Donga György , Fazekas Béla , Fazekas G. , Frankl Péter , Gács Zsuzsa , Gegesy F. , Gerhardt T. , Gönczi I. , Göndőcs Ferenc , Hargitay L. , Kiss Csaba , Lázár András , Lengyel János , Maróti P. , Molnár György , Nagy András , Nagy Dénes , Nikodémusz Anna , Papp László , Papp Zoltán , Prőhle Tamás , Sailer Kornél , Schűgerl Márta , Simon Júlia , Sipos Ferenc , Skopál István , Somorjai Gábor , Szabó György , Szabó Zsolt , Szalontai Árpád , Terjéki József , Turi A. , Tölgyesi Ernő , Viszkei Gy.
Füzet:	1970/november, 102 - 106. oldal		PDF \| MathML
Témakör(ök):	Egyenesek egyenlete, Párhuzamos szelőszakaszok tétele, Feladat
Hivatkozás(ok):	Feladatok: 1968/december: F.1637

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Feltesszük, hogy a $B$ , $D$ , $Q$ pontok létrejöttek, vagyis felvétel folytán $A E$ nem párhuzamos $C F$ -fel, $A F$ nem párhuzamos $C E$ -vel és az adódott $B D$ egyenes nem párhuzamos $e$ -vel.
Messe a $C$ -n át $e$ -vel párhuzamosan húzott $e'$ egyenes $A E$ -t, $A F$ -et, $B D$ -t rendre a $G$ , $H$ , $K$ pontban (létrejönnek, mert az átmetszett egyenesek a föltevések szerint hajlanak $e$ -hez; 1. ábr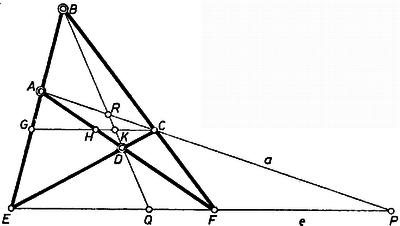a).

1. ábra

A bizonyítás során az

e

e'

egyeneseken létrejött szakaszok alkalmas párjaiból képezett arányokat tekintünk, azt felhasználva, hogy a többi hat egyenes közül az

A

B

és

D

pontok mindegyikén

3 - 3

megy át, vagyis

e

és

e'

három különböző sugárhármast metsz át. A szakaszokon irányításukat is mindig tekintetbe vesszük, tehát

X Y = - Y X

.
A

B

-n, majd a

D

-n átmenő sugárhármas alapján

\begin{matrix} \frac{E Q}{G K} = \frac{Q B}{K B} = \frac{Q F}{K C}, amiből \frac{E Q}{Q F} = \frac{G K}{K C}, \end{matrix}

és ugyanígy

\begin{matrix} \frac{E Q}{Q F} = \frac{C K}{K H} . \end{matrix}

A bal oldalak egyenlősége alapján az

e'

-n levő metszéspontokra

\begin{matrix} \frac{G K}{K C} = \frac{C K}{K H} . \end{matrix}

Mindkét oldalhoz

1

-et adva, majd az aránypárt átrendezve

\begin{matrix} \frac{G C}{K C} = \frac{C H}{K H}, \frac{G C}{C H} = \frac{K C}{K H} . \end{matrix}

(1)

Végül a bal oldali arányt az

A

-n, a jobb oldalit pedig a

D

-n átmenő sugárhármas alapján

e

megfelelő szakaszaival kifejezve

\begin{matrix} \frac{G C}{C H} = \frac{E P}{P F}, \frac{K C}{K H} = \frac{Q E}{Q F} = - \frac{E Q}{Q F}, \end{matrix}

és ezek szerint (1) második egyenlőségéből

\begin{matrix} \frac{E Q}{Q F} = - \frac{E P}{P F} . \end{matrix}

(2)

Megmutatjuk, hogy az

E F

egyenes bármely, az

F

-től különböző

X

pontja egyértelműen meghatározza az

\frac{E X}{X F} = λ

arány (ún. osztóviszony) értékét, és megfordítva, az arány értéke (kivéve, ha

- 1

) egyetlen pontot jelöl ki az egyenesen. Ebből már következik, hogy

P

helyzete (2) útján egyértelműen meghatározza

Q

helyzetét, tehát ezt

a

A

és

C

megválasztása nem befolyásolja.
Amíg ugyanis

X

E

-től

F

-ig halad,

λ > 0

és monoton nő, mert számlálója monoton nő, nevezője monoton csökken.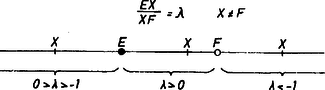

2. ábra

Amíg

X

F

-en túli meghosszabbításon távolodik, az előjel negatív, mert

X F

irányítása ellentétes

E X

-ével, az abszolút érték pedig (2. ábra):

\begin{matrix} | λ | = \frac{E X}{F X} = \frac{E F + F X}{F X} = 1 + \frac{E F}{F X} > 1, \end{matrix}

monoton csökken, tehát

λ

növekszik

- 1

-ig, magát a

- 1

értéket viszont nem veszi fel. Végül akkor is

λ < 0

, ha

X

E

-n túli meghosszabbításon távolodik, és ekkor abszolút értéke

0

-től

1

-ig nő (azaz

0 \geq λ > - 1

\begin{matrix} | λ | = \frac{X E}{X F} = \frac{X F - E F}{X F} = 1 - \frac{E F}{X F}, \end{matrix}

hiszen a kivonandó pozitív, nem nagyobb

1

-nél, és fogy, ha

X F

növekszik.
Megfordítva, ha

λ \neq - 1

, akkor

\begin{matrix} λ = \frac{E X}{X F} = \frac{E F + F X}{X F} = - \frac{E F}{F X} - 1 -ből \\ F X = - \frac{E F}{1 + λ} = \frac{F E}{1 + λ} \end{matrix}

egyértelműen meghatározza

X

helyzetét.
Ezek szerint az

E F

F P

és

P E

szakaszok közti egyenlőség kizárása csak az utóbbi kettő között lényeges; ha ugyanis

P

E F

felezőpontja, akkor (2) jobb oldala

1

és

E Q / Q F = - 1

, kizárt érték, tehát

Q

nem jön létre. (Ekkor, bár ha

B

D

mindegyike létre is jött,

B D

párhuzamos

e

-vel.) Az

E F = F P

és

E F = P E

esetekben

Q

E F

szakasz harmadoló pontjaiban adódik.
Bizonyításunk teljességéhez hozzátartozik annak megmutatása, hogy a fölhasznált sugárhármasok

A

B

D

közös pontja nincs rajta

e'

-n. Ezt az 1. ábra szemlélete alapján fogadtuk el.

A

azért nincs

e'

-n, mert

a

hajlik

e

-hez és

A

C

-től különböző pont.

B

sincs rajta, különben csak

C

-vel azonos lehetne, mert az

e

-hez és ezért

e'

-höz is hajló

F C

egyenes csak egy pontban metszi

e'

-t, ekkor pedig

A

is csak

B

-vel lehetne azonos, mert a (

B

-t meghatározó)

E A

egyenes csak egy pontban metszi

a

-t, tehát

A

azonos volna

C

-vel.

D

-re az utóbbi gondolatmenettel bizonyítunk, a betűk kellő fölcserélésével.

Molnár György (Vác, Sztáron S. Gimn. ) és

Szalontai Árpád (Budapest, Berzsenyi D. Gimn.) dolgozatai alapján

Megjegyzés. A

B

és

D

metszéspontok közül legalább az egyik létrejön. Ha ugyanis

B

nem jön létre, vagyis ha

E A ∥ F C

, akkor

D

mindenesetre létrejön, mert

E

F

C

és

A

egy konvex trapéz csúcsai és ha ebben

E F

szárként szerepel, akkor

D

az átlók metszéspontja; ha pedig

E F

átló, akkor

P

az átlók metszéspontja, de nem felezi

E F

-et, ezért az

E A

C F

alapok különbözők, így pedig a szárak metszik egymást (3. ábra).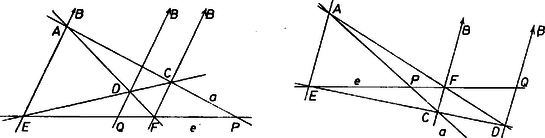

3. ábra

Ebben az esetben meg lehet mutatni, hogy

E F

-nek a

D

-n átmenő,

A E

-vel párhuzamos egyenes által

e

-ből kimetszett

Q

pontjára áll fenn (2).

II. megoldás. Válasszuk derékszögű koordináta-rendszerünk

y

tengelyének magát az

e

egyenest, origójának

P

-t, és legyen

E (0, e)

F (0, f)

, ahol

e 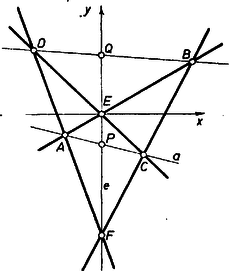\neq f

és

e f \neq 0

(4. ábra).

4. ábra

Legyen továbbá

a

egyenlete

y = m x

(minden

m

-re különböző

e

-től), és

A (a, m a)

C (c, m c)

, ahol

a \neq c

és

a c \neq 0

. (Nem fog félreértést okozni

e

és

a

kétféle jelentése.)
Az

E A

és

F C

egyenes egyenlete:

\begin{matrix} y - e = \frac{m a - e}{a} x, & (3) \\ y - f = \frac{m c - f}{c} x, & (4) \end{matrix}

ezek metszéspontjaként

B

koordinátái:

\begin{matrix} B (\frac{a c (f - e)}{a f - c e}, \frac{m a c (f - e) + e f (a - c)}{a f - c e}), \end{matrix}

(5)

hacsak

a f \neq c e

(

egyenlőségük

\frac{e}{f} = \frac{a}{c} = \frac{m a}{m c}

alakban azt jelentené, hogy

E A ∥ F C)

.
(3)-ban, (4)-ben és (5)-ben minden egyes

e

helyére

f

-et és

f

helyére

e

-t írva,

F A

E C

egyenletét, ill.

D

koordinátáit kapjuk:

\begin{matrix} D (\frac{a c (e - f)}{a e - c f}, \frac{m a c (e - f) + f e (a - c)}{a e - c f}), \end{matrix}

(5')

hacsak

a e \neq c f

(

F A

nem párhuzamos

E C

-vel).
Így a

B D

egyenes egyenlete, majd ebből

Q

ordinátája,

x = 0

helyettesítéssel

\begin{matrix} y - y_{b} = \frac{y_{D} - y_{B}}{x_{D} - x_{B}} (x - x_{B}), \\ y_{Q} = y_{B} - \frac{x_{B} (y_{D} - y_{B})}{x_{D} - x_{B}} = \frac{x_{D} y_{B} - x_{B} y_{D}}{x_{D} - x_{B}} = \\ = \frac{k y_{B} - y_{D}}{k - 1}, ahol k = \frac{x_{D}}{x_{B}} = \frac{c e - a f}{a e - c f} & (6) \end{matrix}

(az osztás megengedett volt, hiszen a fönti kizárások alapján

x_{B} \neq 0

), és

k \neq 1

, ugyanis

k = 1

föltevése

(c - a) (e + f) = 0

-ra,

e = - f

-re vezetne, azaz

E P = P F

-re, amit kizártunk.
Végül (6)-ot kiszámítva

\begin{matrix} y_{Q} = \frac{2 e f}{e + f}, \end{matrix}

ami valóban független

m

a

c

mindegyikétől, és benne, mint legutóbb láttuk,

e + f \neq 0

Papp Zoltán (Debrecen, Fazekas M. Gimn.)

Megjegyzések. 1. Eredményünkből

\begin{matrix} \frac{1}{y_{Q}} & = \frac{e + f}{2 e f} = \frac{1}{2} (\frac{1}{e} + \frac{1}{f}), azaz \\ \frac{1}{P Q} & = \frac{1}{2} (\frac{1}{P E} + \frac{1}{P F}), \end{matrix}

P Q

P E

P F

szakaszok harmonikus közepe, eszerint feladatunk újabb^{$^{*}$} eljárást adott két szakasz harmonikus közepének szerkesztésére ‐ éspedig egyetlen egyenes vonalzó felhasználásával ‐, és akkor is, ha a szakaszok ellentétes irányításúak (de abszolút értékben különbözők).
2. Ebben a bizonyításban így adódik, hogy

B

és

D

közül legalább az egyik létrejön:

a e = c f

és

c e = a f

egyidejű föltevéséből szorzással

a c e^{2} = a c f^{2}

e = - f

, amit mint már láttuk, kizárt.
Ha pedig

B

nem jön létre, azaz

a f = c e

, akkor az

A E

egyenessel párhuzamos és

D

-n átmenő egyenesnek az

y

tengellyel való metszéspontjához tartozó ordináta (nem sok számítással)

\begin{matrix} y = y_{D} + \frac{m a - e}{e} (- x_{D}) = \frac{2 e f}{e + f}, \end{matrix}

amint az I. megoldáshoz fűzött megjegyzés végén állítottuk.
3. Többen fölismerték, hogy a feladat állítása egy, a projektív geometria^{$^{*}$} elemeiben tárgyalt alapvető tétel: az

A B

B C

C D

D A

egyenesekkel meghatározott, ún. teljes négyoldal (amelynek még

E

és

F

is szögpontjai) átlóján levő két szögpont és két átlós pont harmonikusan választja szét egymást, amin ezt értik:

\begin{matrix} (\frac{E Q}{Q F}) : (\frac{E P}{P F}) = - 1. \end{matrix}

(A teljes négyoldal

3

átlója:

E F

B D

és

A C

, az utóbbi kettőnek

R

metszéspontja is átlós pont.)

^{$^{*}$}Lásd az 1169. gyakorlatot, K. M. L. 37 (1968) 70. o., valamint a hozzá kapcsolódó cikket: Tusnády Gábor: Az 1169. gyakorlat megoldása vektorok segítségével, K. M. L. 37 (1968) 49‐51. o.

^{$^{*}$}Lásd a következő Középiskolai Szakköri Füzetekben (kiadta a Tankönyvkiadó Budapesten): Vigassy Lajos: Projektív geometria, 1970; Vigassy Lajos: Geometriai transzformációk, 1963.