Kezdőlap


Feladat:	F.1632	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bajmóczy Ervin , Beck J. , Donga Gy. , Gőgh J. , Kóczy L. , Lukács P. , Máté András , Nagy D. , Sailer K. , Szalontai Á. , Viszkei Gy.
Füzet:	1969/november, 104 - 107. oldal		PDF \| MathML
Témakör(ök):	Tengelyes tükrözés, Pont körüli forgatás, Ceva-tétel, Simson-egyenes, Szinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1968/november: F.1632

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. a) Jelöljük $P$ tükörképét a háromszög $A$ -nál, $B$ -nél, $C$ -nél levő szögének felezőjére sorra $P_{1}$ -gyel, $P_{2}$ -vel, $P_{3}$ -mal. A kívánt $A P_{1}$ , $B P_{2}$ , $C P_{3}$ tükörképeket két-két, az $A$ , $B$ , ill. $C$ pont körüli elfordítással állítjuk elő. Pozitívnak azt a forgási irányt vesszük, amely az $A B$ félegyenest $180^{\circ}$ -nál kisebb elfordulással viszi át 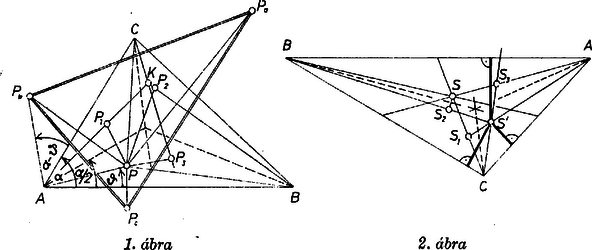$A C$ -be.
Legyen $B A C ∢ = α$ és $B A P ∢ = ϑ$ (1. ábra). Ekkor $A P$ -t a $B A C$ szög felezőjébe $α / 2 - ϑ$ nagyságú elfordulás viszi át, az előírt $A P_{1}$ helyzetbe pedig $2$ -szer ekkora elfordulás: $α - 2 ϑ$ . $A P$ -nek első lépésül $- 2 ϑ$ -val való elfordítása az $A B$ -n való tükrözését jelenti az $A P_{c}$ helyzetbe, ahol $P_{c}$ a $P$ tükörképe $A B$ -re, második lépésül ezt $α$ -val fordítjuk el. ‐ Ugyanezt a véghelyzetet kapjuk, ha $A B$ -t $A C$ -vel felcserélve, $A P$ -t $A C$ -re tükrözzük az $A P_{b}$ helyzetbe, ami $2 (α - ϑ)$ -val történő elfordítás, majd a képet $- α$ -val fordítjuk el. Ezek szerint az $A P_{1}$ félegyenes felezi a $P_{c} A P_{b}$ szöget¹, pontosabban az $A P_{c}$ -ből $A P_{b}$ -be vivő elfordulást. És mivel $A P_{c} = A P = A P_{b}$ , ezt is mondhatjuk: $A P_{1}$ a $P_{c} P_{b}$ szakasz felező merőlegese.
Ugyanígy, $P$ tükörképét $B C$ -re $P_{a}$ -val jelölve $B P_{2}$ a $P_{a} P_{c}$ szakasz felező merőlegese, $C P_{3}$ pedig a $P_{a} P_{b}$ szakaszé, vagyis a vizsgálandó $A P_{1}$ , $B P_{2}$ , $C P_{3}$ egyenesek a $P_{a} P_{b} P_{c}$ háromszög oldalfelező merőlegesei, tehát ennek a háromszögnek $K$ középpontjában metszik egymást ‐ hacsak a mondott háromszög nem fajult el egyenesszakasszá. Ezt kellett bizonyítanunk; tehát az állításbeli $P'$ pont $K$ .

P

-ként az

A B C

háromszög

M

magasságpontját választva

P'

-ként ‐ a fenti

K

helyén ‐ az

A B C

háromszög köré írt

k

kör

O

középpontját kapjuk, hiszen ekkor ‐ mint jól ismert ‐ a

P_{a}

P_{b}

P_{c}

tükörképek

k

-n adódnak. Minthogy pedig egy tükörkép egyenesnek ugyanazon tengelyre vett tükörképe az eredeti egyenes,

O

-t véve

P

-ként,

P'

-ként

M

-et kapjuk, vagyis a háromszög ezen két nevezetes pontját a feladatban vizsgált eljárás egymásba viszi át.

P

-ként az

S

súlypontot választva, megmutatjuk a tétel szerint kapott

P' = S'

pont következő tulajdonságát:

S'

az a pontja a háromszög síkjának, amelynek az egymás utáni oldalaktól mért távolságai arányosak a megfelelő oldalak hosszával. Ehhez belátjuk, hogy az

S

pont

B A C ∢

szögfelezőjére vett

S_{1}

tükörképének az

A B

A C

oldalaktól mért

d_{c}

d_{b}

távolságaira fennáll

d_{c} : d_{b} = c : b

, és természetesen ugyanez az aránya az

A S_{1}

egyenes minden

S^{*}

pontja távolságainak a mondott oldalaktól. Ebből már következik, hogy

A S_{1}

-nek az analóg

B S_{2}

-vel való

S'

metszéspontjára

d'_{c} : d'_{b} = c : b

és

d'_{a} : d'_{c} = a : c

, tehát

d'_{a} : d'_{b} : d'_{c} = a : b : c

.
A súlypont ismert harmadoló tulajdonsága miatt

S

-nek az

A B

A C

oldaltól mért távolsága az

m_{c}

, ill.

m_{b}

magasság

1 / 3

részével egyenlő (2. ábra), így

S_{1}

re nézve

d_{c} = m_{b} / 3

d_{b} = m_{c} / 3

, és mivel még

m_{b} = 2 t / b

m_{c} = 2 t / c

, ahol

t

a háromszög területe,

d_{c} : d_{b} = 2 t / 3 b : 2 t / 3 c = c : b

Bajmóczy Ervin (Budapest, Fazekas M. Gyak. Gimn., II. o. t.)

Máté András (Budapest, I. István Gimn., I. o. t.)

Megjegyzés. Ha ismerjük a következő tételt, akkor megadhatjuk, mely

P

pontok esetén jön létre

P'

. Egy

P

pontnak az

A B C

(nem elfajult) háromszög oldalegyenesein levő

Q_{a}

Q_{b}

Q_{c}

vetületei akkor és csak akkor vannak egy egyenesen, ha

P

a háromszög köré írt

k

kör kerületén van (az egyenes a háromszöghöz és a

P

ponthoz tartozó Simson-féle ‐ más névvel Wallace-féle ‐ egyenes)². Mármost

P_{a}

P_{b}

P_{c}

Q_{a}

Q_{b}

Q_{c}

ponthármas

2

-szeresre nagyított képe

P

-ből mint középpontból, tehát a

P_{a} P_{b} P_{c}

háromszög akkor és csak akkor fajul el egyenessé ‐ és így

P'

nem jön létre ‐, ha

P

k

-n van (3. ábra).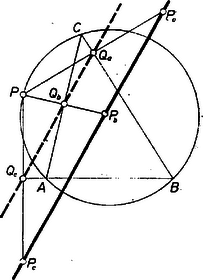

3. ábra

II. megoldás. Messe a

B C

C A

A B

oldalt a

P A

P B

P C

egyenes rendre az

A_{1}

B_{1}

C_{1}

pontban (4. ábra), a szóban forgó tükörképük pedig rendre az

A_{2}

B_{2}

C_{2}

p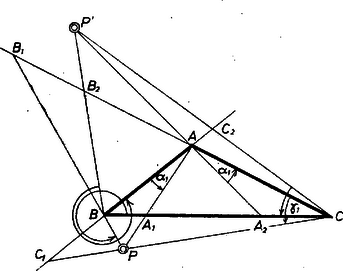ontban.

4. ábra

Egyelőre feltesszük, hogy mindegyik metszéspont létrejött. Ekkor Ceva tétele³ szerint fennáll

\begin{matrix} \frac{A C_{1} \cdot B A_{1} \cdot C B_{1}}{C_{1} B \cdot A_{1} C \cdot B_{1} A} = 1, \end{matrix}

(1)

és azt kell bebizonyítanunk, hogy teljesül a következő is:

\begin{matrix} \frac{A C_{2} \cdot B A_{2} \cdot C B_{2}}{C_{2} B \cdot A_{2} C \cdot B_{2} A} = 1. \end{matrix}

(2)

Legyen az

A B C

háromszög körüljárása pozitív (vagyis pl.

A B

-t

A C

-be,

180^{\circ}

-nál kisebb szöggel, pozitív forgás viszi át), és a

B A P

C B P

A C P

forgásszög mértékszáma rendre

α_{1}

β_{1}

γ_{1}

, ekkor szerkesztésnél fogva ugyanennyi (esetleg

180^{\circ}

-kal több vagy kevesebb) a

B A A_{1}

C B B_{1}

A C C_{1}

szög mértékszáma, úgyszintén az

A_{2} A C

B_{2} B A

C_{2} C B

szög mértékszáma is. Az

A A_{1} B

és

A A_{1} C

háromszögekből a sinustétel alapján

\begin{matrix} \frac{B A_{1}}{A_{1} C} = \frac{B A sin α_{1}}{sin (β + α_{1})} : \frac{A C sin (α - α_{1})}{sin (β + α_{1})} = \frac{B A sin α_{1}}{A C sin (α - α_{1})}, \end{matrix}

hasonlóan a

B B_{1} C

B B_{1} A

, valamint

C C_{1} A

C C_{1} B

háromszögpárokból

\begin{matrix} \frac{C B_{1}}{B_{1} A} = \frac{C B sin β_{1}}{B A sin (β - β_{1})}, \frac{A C_{1}}{C_{1} B} = \frac{A C sin γ_{1}}{C B sin (γ - γ_{1})}, \end{matrix}

(3)

és ezekkel az (1) feltevés így alakul

\begin{matrix} \frac{sin α_{1} sin β_{1} sin γ_{1}}{sin (α - α_{1}) sin (β - β_{1}) sin (γ - γ_{1})} = 1. \end{matrix}

(4)

Másrészt az

A A_{2} B

A A_{2} C

, valamint

B B_{2} C

B B_{2} A

és

C C_{2} A

C C_{2} B

háromszögpárokból

\begin{matrix} \frac{B A_{2}}{A_{2} C} = \frac{B A sin (α - α_{1})}{A C sin α_{1}}, \frac{C B_{2}}{B_{2} A} = \frac{C B sin (β - β_{1})}{B A sin β_{1}}, \\ \frac{A C_{2}}{C_{2} B} = \frac{A C sin (γ - γ_{1})}{C B sin γ_{1}}, \end{matrix}

ezek szorzata pedig (4) figyelembevételével (2)-t adja, amit bizonyítani akartunk.
Ha a

P A

P B

P C

egyenesek, ill. szóban forgó tükörképük közül egy vagy több párhuzamos a háromszög megfelelő oldalával, speciális esetek adódnak, ezekben a bizonyítás egyszerűbben alakul. Példaként csak a

P A | | B C

esetet vesszük (

P B

P C

ne legyen párhuzamos oldallal, és

A_{2}

B_{2}

C_{2}

is jöjjenek létre, 5. ábra).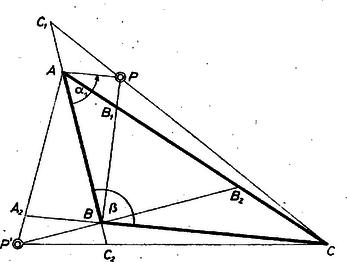

5. ábra

Ekkor

A

B

C

P

egy trapéz csúcsai, és hasonló háromszögekből

\begin{matrix} \frac{A C_{1}}{C_{1} B} = \frac{A P}{B C}, \frac{C B_{1}}{B_{1} A} = \frac{B C}{A P}, \end{matrix}

tehát szorzatuk

1

. Másrészt, ha

P

A B

egyenesnek ugyanazon az oldalán van, mint

C

, akkor

α_{1} = 180^{\circ} - β

, így a (3) jobb oldalain álló kifejezések szorzatát megszorozva

\begin{matrix} \frac{B A sin β}{A C sin γ} \end{matrix}

-val, aminek értéke

1

, és így is írható:

\begin{matrix} \frac{B A sin (180^{\circ} - β)}{A C sin (α + β - 180^{\circ})} = \frac{B A sin α_{1}}{A C sin (α - α_{1})}, \end{matrix}

ismét megkapjuk (4)-et.

¹Az 1. ábrán az

A P_{c}

egyenesdarab pótlandó.

²A feltétel elegendő volta bizonyítását speciális esetre lásd pl. Faragó László-Forgó Péterné: Geometriai szerkesztések, 2. kiadás (Középiskolai Szakköri Füzetek), Tankönyvkiadó, Budapest, 1954, 103. o.

³Lásd az 1437. feladathoz fűzött megjegyzést, K. M. L. 33 (1966) 207. o., legutóbb felhasználva az 1119. gyakorlatban, K. M. L. 36 (1968) 158. o. (1) megfordítva is érvényes: ha (1) teljesül, akkor $A A_{1}$ , $B B_{1}$ , $C C_{1}$ egy ponton mennek át.