Kezdőlap


Feladat:	F.1631	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Dombi G. , Donga György , Fialovszky Alice , Fischer Ágnes , Galántai A. , Gegesy F. , Gerhardt T. , Graffjódi L. , Hegyi Gy. , Loványi I. , Máté A. , Nagy András , Nagy Dénes , Petravich G. , Posgy K. , Radványi Katalin , Simon Júlia , Szalai G. , Szalontai Á. , Tóth Attila , Várhegyi Éva , Zambó Péter
Füzet:	1970/április, 145 - 149. oldal		PDF \| MathML
Témakör(ök):	Százalékszámítás, Numerikus és grafikus módszerek, Terület, felszín, Számtani sorozat, Feladat
Hivatkozás(ok):	Feladatok: 1968/november: F.1631

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Az $a$ oldalú szabályos háromszög alapjára $n$ db $r$ sugarú kört írva az 1c) ábra szerint

\begin{matrix} a = 2 \cdot r \sqrt[]{3} + (n - 1) \cdot 2 r, \end{matrix}

\begin{matrix} r = \frac{a}{2 (n - 1 + \sqrt[]{3})}, \end{matrix}

és a sorok száma ugyancsak

n

. Ezért a körök együttes száma

1 + 2 + ... + n = n (n + 1) / 2

, a lefedett terület

\begin{matrix} \frac{n (n + 1)}{2} \cdot \frac{π a^{2}}{4 {(n - 1 + \sqrt[]{3})}^{2}}, \end{matrix}

és ennek aránya a háromszög

a^{2} \sqrt[]{3} / 4

területéhez

\begin{matrix} q_{n} = \frac{π}{2 \sqrt[]{3}} \cdot \frac{n (n + 1)}{{(n - 1 + \sqrt[]{3})}^{2}} (= \frac{50 π}{\sqrt[]{3}} \cdot \frac{n (n + 1)}{{(n + \sqrt[]{3} - 1)}^{2}} %) . \end{matrix}

(1)

n = 1,2 és 3

esetében, egészre kerekítve rendre 60%, 73%, 79%.

1. ábra

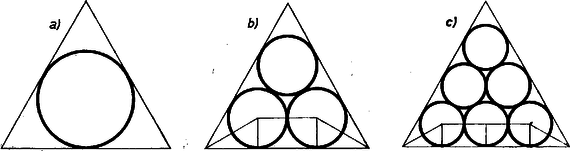II. Eredményünk így alakítható:

\begin{matrix} q_{n} = \frac{π}{2 \sqrt[]{3}} (1 - \frac{(2 \sqrt[]{3} - 3) n + (4 - 2 \sqrt[]{3})}{{(n + \sqrt[]{3} - 1)}^{2}}) . \end{matrix}

Itt a zárójelbeli kivonandó nagy

n

-ekre várhatóan kevéssel különbözik a

(2 \sqrt[]{3} - 3) / n

törttől ‐ ami úgy keletkezik, hogy a számlálóban is, a nevezőben is csak azt a tagot tartjuk meg, amely

n

-et a legmagasabb hatványán tartalmazza. Egyszerű számítás mutatja, hogy a módosított tört és az eredeti tört különbsége nagyobb, mint

\begin{matrix} \frac{14 - 8 \sqrt[]{3}}{{(n + \sqrt[]{3} - 1)}^{2}} > 0, \end{matrix}

tehát

\begin{matrix} q_{n} > \frac{π}{2 \sqrt[]{3}} (1 - \frac{2 \sqrt[]{3} - 3}{n}) . \end{matrix}

Azt kell biztosítanunk, hogy a jobb oldal nagyobb legyen

0, 9

-nél:

\begin{matrix} n > \frac{π (2 \sqrt[]{3} - 3)}{π - 2 \cdot 0, 9 \sqrt[]{3}} \approx 61, \end{matrix}

a körök tehát biztosan lefedik a háromszög területének 90%-át, ha egy oldalon legalább 62-t veszünk belőlük. (Természetesen a

π = 3, 1416

közelítő értéket használtuk, mert

1, 8 \sqrt[]{3} = \sqrt[]{9, 72} \approx 3, 1177 \approx 3, 12

miatt a

3, 14

-es közelítő értékkel a nevezőben csak egy értékes jegyünk lenne.)

III. A négyzetbe írt körök esetében rajzoljuk meg az érintkező körök közös érintőjét a kör legközelebbi érintőjével való metszéspontig, ill. a négyzet kerületéig. Így a 2a) ábra minden köre körül ismét négyzet jön létre, a 2b) ábra körei körül viszont a körülírt szabályos hatszögük, amennyiben a kör 6 másik körrel érintkezik, különben pedig egy ötszög vagy trapéz.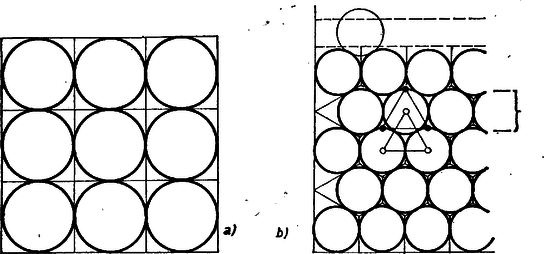

2. ábra

A 2a) ábra esetében a fedési arány bármely

n

esetében ugyanannyi, ti.

\begin{matrix} n^{2} {(\frac{b}{2 n})}^{2} π : b^{2} = \frac{π}{4} = 0, 785 \end{matrix}

(

b

a négyzet oldala). Így

0, 9

-es fedés nem érhető el.
A 2b) ábra esetében

n = 2

-re és

3

-ra az arány kisebb ennél, hiszen ekkor a 2a) ábra szerinti 4, ill. 9 kör helyett csak 3-at, ill. 8-at tudunk berajzolni. Ennek ellenére

n

-et elég nagyra választva a

0, 9

-es fedés ‐ mint majd látjuk ‐ túlléphető. Ehhez előrebocsátjuk a következőket.

n

növelésével várható, hogy

n

-nél több sor rétegezhető egymás fölé, így ellensúlyozódik az a veszteség, hogy a páros sorszámú sorok 1-gyel kevesebb kört tartalmaznak.
Másrészt egy

r

sugarú kör a köréje írt szabályos hatszög területéből többet fed le, mint

0, 9

rész, hiszen a hatszög oldala

c = 2 r / \sqrt[]{3}

, területe

3 \sqrt[]{3} c^{2} / 2 = 2 \sqrt[]{3} r^{2}

, és

π r^{2}

-et ezzel osztva

\begin{matrix} \frac{π}{2 \sqrt[]{3}} = 0, 9069. \end{matrix}

Végül a 6-nál kevesebb körrel érintkező körök az érintődarabok által köréjük írt sokszög területéből ennél ugyan kisebb hányadrészt fednek le, várható viszont, hogy

n

növelésével a négyzet kerülete közelében lefedetlenül maradt terület csökken. (Hasonlóan, mint az 1. ábra, szerinti berajzolás esetében, hiszen a 2b ábrán a körök kölcsönös helyzete az 1. ábra szerinti.)
Rátérve a számításra, írjunk az alapra

n

kört és legyen a körökből álló vízszintes sorok száma

N

. Az alsó sorbeli körök legmagasabb pontja

2 r = b / n

magasságban van a négyzet alapja fölött, és ez a magasság sorról sorra

r \sqrt[]{3}

-mal lesz több, ti. ennyi a 3, páronként érintkező kör középpontjai által meghatározott háromszög magassága. Így az alsó sor fölé annyi további sor rétegezhető, amennyi a

(b - 2 r) / \sqrt[]{3}

hányados egész része:

\begin{matrix} N - 1 = [\frac{b - 2 r}{r \sqrt[]{3}}] = [\frac{2 (n - 1)}{\sqrt[]{3}}] . \end{matrix}

Aszerint, hogy

N

páros, ill. páratlan, a berajzolt körök száma

\begin{matrix} K_{n} = \frac{N}{2} (2 n - 1), ill. \frac{N - 1}{2} (2 n - 1) + n, \end{matrix}

hiszen két szomszédos sorban

n + (n - 1)

kör van. Ebből a lefedett terület kiszámítható.
Vegyük példának

n = 7

és

n = 8

esetét.

\begin{matrix} N_{7} - 1 = [\frac{2 \cdot 6}{\sqrt[]{3}}] = [4 \sqrt[]{3}] = [6, 928] = 6, \end{matrix}

\begin{matrix} N_{8} - 1 = [\frac{14}{\sqrt[]{3}}] = [8, 082] = 8, \end{matrix}

vagyis a sorok száma 7, ill. 9 (az áttérésben 2-vel nőtt), közülük a rövidebbek száma 3, ill. 4, igy a körök száma

\begin{matrix} K_{7} = 7 \cdot 7 - 3 = 46, ill. K_{8} = 9 \cdot 8 - 4 = 68, \end{matrix}

és a lefedési arány

\begin{matrix} \frac{46}{49} \cdot \frac{π}{4} = 0, 737, ill. \frac{68}{64} \cdot \frac{π}{4} = 0, 835. \end{matrix}

A növekedést az is magyarázza, hogy

n = 7

esetében a felső sor fölött olyan sáv maradt üresen, amelynek szélessége a körátmérőnek

0, 928

-szerese, amennyit az egész rész képezésekor elhagytunk, viszont

n = 8

esetében ez az arány csak

0, 082

.
Jelöljük

μ

-vel azoknak a soroknak a számát, amelyekben csak

n - 1

kör van, ezt

n

-nel becsüljük:

\begin{matrix} μ \leq \frac{N + 1}{2} \leq \frac{\frac{2}{\sqrt[]{3}} (n - 1) + 2}{2} < (n - 1) + 1 = n . \end{matrix}

Ezt felhasználva

\begin{matrix} q_{n} = \frac{(n \cdot N - μ) π r^{2}}{b^{2}} > (n N - n) π {(\frac{r}{b})}^{2} > \frac{\frac{2}{\sqrt[]{3}} (n - 1) - 1}{n} \cdot \frac{π}{4} = (1 - \frac{1 + \frac{\sqrt[]{3}}{2}}{n}) \cdot \frac{π}{2 \sqrt[]{3}}, \end{matrix}

ami nagyobb

0, 9

-nél, ha

\begin{matrix} n > \frac{π (1 + \frac{\sqrt[]{3}}{2})}{π - 2 \cdot 0, 9 - \sqrt[]{3}} \approx 246. \end{matrix}

Pl.

n = 250

esetén

N - 1 = [166 \sqrt[]{3}] = [287, 52] = 287, K_{n} = 71 928, q_{n} = 0, 9038

Donga György (Budapest, Berzsenyi D. Gimn.)

dolgozatának felhasználásával, számos kiegészítéssel

Megjegyzések. 1. A háromszögbe írt körök esetében

n

növekedésével

q_{n}

‐ mint arra fent csak céloztunk ‐ valóban monoton nő, ugyanis

\begin{matrix} \frac{q_{n + 1}}{q_{n}} = \frac{(n + 2) {(n + \sqrt[]{3} - 1)}^{2}}{{(n + \sqrt[]{3})}^{2} n} = \frac{n^{3} + 2 \sqrt[]{3} n^{2} + 2 \sqrt[]{3} n + 4 (2 - \sqrt[]{3})}{n^{3} + 2 \sqrt[]{3} n^{2} + 3 n} = \\ = 1 + \frac{(2 \sqrt[]{3} - 3) n + 4 (2 - \sqrt[]{3})}{{(n + \sqrt[]{3})}^{2} n} > 1, \end{matrix}

hiszen a számlálóbeli együtthatók pozitívok.

2. A háromszögbe írt körök esetében a becsléssel talált

n \geq 62

eredményt megkaphatjuk a

q_{n} = 0, 9

(másodfokúra vezető) egyenlet megoldásával is, pozitív gyökét (

\approx 60, 5

) a legközelebbi egész számra fölkerekítve. Valóban, nagyobb pontosságú számítással

q_{60} = 0, 89992, q_{61} = 0, 90003

.
3. A négyzetbe írt körök esetére megmutatjuk, hogy

n

-ről

2 n

-re áttérve a fedettségi arány csak nőhet.

r = b / n

esetén a második sorbeli

n - 1

kör legfelső pontjának magassága

\begin{matrix} r (2 + \sqrt[]{3}) = \frac{2 + \sqrt[]{3}}{2 n} \cdot b = \frac{b}{n} (1 + \frac{\sqrt[]{3}}{2}) = \frac{b}{n} 1, 866, \end{matrix}

viszont

r = b / 2 n

esetén a 4. sorbeli körök legfelső pontja alacsonyabban van:

\begin{matrix} \frac{r}{2} (2 + 3 \sqrt[]{3}) = \frac{b}{n} \cdot 1, 799, \end{matrix}

és az eddig elhelyezett körök száma 2n-1-ről több mint a 4-szeresére emelkedett:

2 (2 n + 2 n - 1) = 8 n - 2

-re.
Utóbbi megállapításunk két, ill. 4 szomszédos magasabb sor esetére is érvényes, de itt a 2, ill. 4 sor szélessége (alsó és felső pontjaik egyenesének távolsága) ugyanannyi.
Végül a kétféle kitöltést 1, ill. 2 soros sávonként folytatva előfordulhat, hogy

b / n

sugarú körből már nem fér be 1 sor, de

b / 2 n

sugarúból befér.
Ezek szerint, ha egy

n

érték esetén a fedés több, mint 90%, akkor mondhatjuk, hogy tetszés szerinti számú olyan

n

érték van.