Kezdőlap


Feladat:	F.1627	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Bajmóczy E. , Bauer Katalin , Boda S. , Donga Gy. , Farkas Gy. , Fazekas Béla , Fazekas Gábor , Fischer Ágnes , Füredi A. , Gajdács Ibolya , Gegesy F. , Gönczi I. , Göndőcs F. , Horváth Gyula , Joó G. , Kabos S. , Kánya Olga , Kerekes J. , Komjáth P. , Krasznai András , László I. , Láz J. , Lukács Péter , Magyar Á. , Maróti P. , Martoni V. , Morvai I. , Munka Margit , Nagy Dénes , Nikodémusz Anna , Papp Z. , Petravich G. , Pintér Vera , Prőhle T. , Pukler A. , Schván P. , Simon Júlia , Szabó György , Szabó Katalin , Szalay Csilla , Szalontai Á. , Szamosújvári Sándor , Tél T. , Török Gyula , Várhegyi Éva , Viszkei Gy. , Zachar Z.
Füzet:	1969/május, 199 - 204. oldal		PDF \| MathML
Témakör(ök):	Mozgással kapcsolatos szöveges feladatok, Feladat
Hivatkozás(ok):	Feladatok: 1968/október: F.1627

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a járműveket $J_{i}$ -vel, útvonalaikat $u_{i}$ -vel, ahol $i = 1, 2, 3, 4$ , az $u_{k}, u_{m}$ útvonalak metszéspontját $(m > k) M_{k m}$ -mel 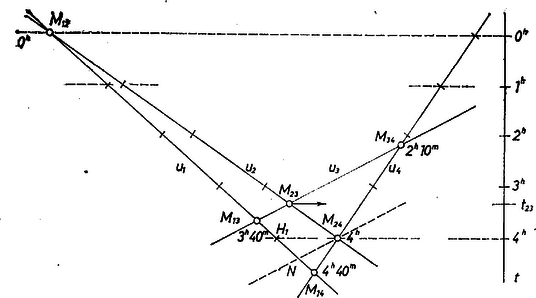(1. ábra).

1. ábra

A találkozási időadatok és a sebességek állandó iránya alapján

M_{14} M_{13} < M_{14} M_{12}

és

M_{14} M_{24} < M_{14} M_{34}

, ezért az

u_{2}, u_{3}

útvonalpár metszi egymást és

M_{23}

egyrészt

M_{12}

és

M_{24}

, másrészt

M_{34}

és

M_{13}

között van. Megmutatjuk, hogy

J_{2}

-nek és

J_{3}

-nak

M_{23}

-on való áthaladási időpontja megegyezik.
Jelöljük

J_{i}

-nek 1 perc alatt megtett útját

v_{i}

-vel, így a sebességek számértékének állandó volta alapján 4

M_{12}

M_{13}

=220

v_{1}

M_{13}

M_{14}

=60

v_{1}

;

M_{24}

M_{14}

=40

v_{4}

M_{34}

M_{14}

=150

v_{4}

;

M_{12}

M_{24}

=240

v_{2}

;

M_{34}

M_{13}

=90

v_{3}

.
Messe az

u_{3}

-mal

M_{24}

-en át húzott párhuzamos

u_{1}

-et (

M_{13}

és

M_{14}

között, hiszen

M_{14}

ugyanazon oldalán van

u_{3}

-nak, mint

M_{24}

)

N

-ben, ekkor a szög szárait metsző párhuzamosok tételeit előbb az

M_{12} M_{14} M_{34}

szögre, majd az

M_{14} M_{12} M_{24}

szögre alkalmazva egyrészt

\begin{matrix} N M_{14} : M_{13} M_{14} = M_{24} M_{14} : M_{34} M_{14} és N M_{24} : M_{13} M_{34} = M_{14} M_{24} : M_{14} M_{34}, \end{matrix}

amiből a fenti értékekkel

\begin{matrix} N M_{14} = M_{13} M_{14} \cdot \frac{M_{24} M_{14}}{M_{34} M_{14}} = 16 v_{1}, ill. N M_{24} = M_{13} M_{34} \cdot \frac{M_{14} M_{24}}{M_{14} M_{34}} = 24 v_{3}, \end{matrix}

és így

M_{13} N = 44 v_{1}, M_{12} N = 264 v_{1},

másrészt

\begin{matrix} M_{23} M_{12} : M_{24} M_{12} = M_{23} M_{13} : M_{24} N & = M_{13} M_{12} : N M_{12} = 220 v_{1} : 264 v_{1} = 5 : 6, \end{matrix}

amiből

\begin{matrix} M_{23} M_{12} = \frac{5}{6} M_{24} M_{12} = 200 v_{2}, és M_{23} M_{13} = \frac{5}{6} M_{24} N = 20 v_{3} . \end{matrix}

Ezek szerint az

M_{12} M_{23}

utat

J_{2}

200 perc alatt teszi meg,

M_{23}

-on éjfél után 200 perccel, azaz

3^{h} 20^{m}

-kor halad át,

J_{3}

pedig az

M_{13}

-beli

3^{h} 40^{m}

-es találkozása előtt 20 perccel, vagyis ugyancsak

3^{h} 20^{m}

-kor. ‐ Ezzel a megoldást befejeztük.
Krasznai András (Gyöngyös, Vak Bottyán Gimn., IV. o. t.)

Megjegyzés. Számításunkat részben megismételjük a lényegében azonos, egyszerűbb betűzésű

1'

ábrához kapcsolódva, ahol az

A B C

háromszög

A B, B C, C A

oldalegyenesét az

u_{3}

egyenes rendre a

C_{1}, A_{1}, B_{1}

pontban metszi és

D C | | C_{1} A_{1}

. Ebből két módon kifejezve, ezeket egyenlővé téve, majd az első kifejezést a másodikkal osztva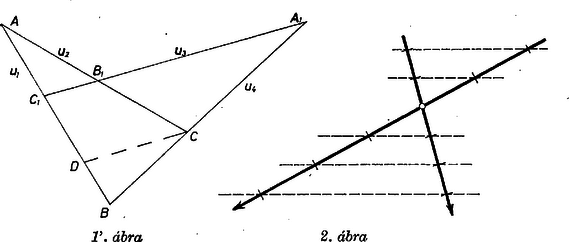

\begin{matrix} C_{1} D = A_{1} C \cdot \frac{C_{1} B}{A_{1} B} = B_{1} C \cdot \frac{A C_{1}}{A B_{1}}, \frac{A B_{1}}{B_{1} C} \cdot \frac{B C_{1}}{C_{1} A} \cdot \frac{C A_{1}}{A_{1} B} = 1, \end{matrix}

az ún. Menelaosz-féle tételt kaptuk. (A szakaszokat a háromszög körüljárása mentén irányítva a tétel tulajdonképpen azt mondja, hogy a 3 hányados szorzatának értéke ‐1; ugyanis egy a háromszög mindhárom oldalegyenesétől különböző egyenes vagy két pontban metszi a kerületet és ekkor egy oldal meghosszabbítását metszi, vagy mindhárom oldal meghosszabbítását metszi, és minden ilyen esetben a megfelelő hányados negatív, pl. az ábrán

C A_{1}

és

A_{1} B

ellentétes irányúak, míg az első két hányados pozitív, mert az

A C

és

A B

oldal szeletei egyirányúak.)

Esetünkben

B C_{1} / C_{1} A = 60 / 220 = 3 / 11, C A_{1} / A_{1} B = 110 / 150

, ezeket behelyettesítve

A B_{1} / B_{1} C = 5

, másrészt

A B_{1} + B_{1} C = 240 v_{2}

, így

A B_{1} = 200 v_{2}

.
Alkalmazzuk másrészt a tételt az

A_{1} B C_{1}

háromszögre, szelőnek véve

u_{2}

-t:

\begin{matrix} \frac{A_{1} B_{1}}{B_{1} C_{1}} \cdot \frac{C_{1} A}{A B} \cdot \frac{B C}{C A_{1}} = 1, \end{matrix}

amiből

A_{1} B_{1} / B_{1} C_{1} = 7 / 2

, továbbá

A_{1} B_{1} + B_{1} C_{1} = 90 v_{2}

, így

A_{1} B_{1} = 70 v_{2}

.
Ezeket időre átszámítva mindkét esetben

3^{h} 20^{m}

adódik áthaladási időpontnak.

II. megoldás a feladat első részére. Az időpont kiszámítása nélkül bizonyítjuk, hogy

J_{2}

és

J_{3}

találkoztak.
Nyilvánvaló, hogy ha két egyenesvonalú, egyenletes mozgást végző testről tudjuk, hogy ‐ bár útvonalaik különbözők ‐ találkoztak, vagyis utaik kereszteződésén egyszerre haladtak át, akkor bármely időpontban megrajzolva a testeket összekötő egyenest, ennek iránya mindig ugyanaz, és mindkét út írányától különböző (2. ábra).
Ha a feltevések 3 testre páronként érvényesek, akkor a 3 test bármely időpontban egy egyenesen helyezkedik el, mert ‐ a kimondott eredményt a

J_{1}, J_{2}, J_{4}

hármasra alkalmazva ‐

J_{1} J_{2}

iránya is,

J_{1} J_{4}

iránya is állandó, és a

J_{2}, J_{4}

találkozás

t_{24}

időpontjában közös pontjuk van:

M_{24}

. Ugyanez áll a

J_{1}, J_{3}, J_{4}

hármasra, s mivel

J_{1}

és

J_{4}

mindkét hármasnak tagja, mind a négy járműre. Ezért

u_{2}

és

u_{3}

metszéspontján

J_{2}

és

J_{3}

egyszerre haladt át.
Lukács Péter (Budapest, Fazekas M. Gyak. Gimn., II. o. t.)

Megjegyzés. A bizonyítást kiegészíthetjük a találkozási

t_{23}

időpont grafikus meghatározásává (1. ábra).
Ehhez alapot ad egy az útvonalakról szerkesztett mérethű térképvázlat, miután megválasztottuk az

u_{1}, u_{4}

közti

φ

szöget, továbbá

v_{1}

és

v_{4}

arányát. Könnyű ezen kijelölni

J_{1}

-nek

4^{h}

-kor elfoglalt

H_{1}

helyzetét, ami

M_{13} M_{14}

-nek első harmadoló pontja (vagy

J_{4}

-nek

2^{h}

-kor, majd

0^{h}

-kor elfoglalt helyzetét), s ekkor a 4 pontot állandóan felfűző

f

egyenes

4^{h}

-kor a

H_{1} M_{24}

helyzetben van.
Mármost

f

-re bárhol merőlegest ‐ időtengelyt ‐ állítva, ezen pl.

M_{12}

és

H_{1}

vetülete meghatározza az időskálát, végül

M_{23}

, vetületében leolvashatjuk

t_{23}

értékét.
Az olvasóra hagyjuk a mondottak bizonyítását (aminek természetesen azt is tartalmaznia kell, hogy az eredmény független

φ

és a

v_{1} : v_{4}

arány megválasztásától).

III. megoldás a feladat első részére. Gondoljuk, hogy mind a négy jármű éjfélkor indult el és ugyanakkor mindegyikről felszállt egy madár, ezek mindegyike a maga járműve fölött repült és a 4 madár közös sebességgel emelkedett fölfelé. Így a madarak

m_{i}

pályái is egyenesek és az adatok szerinti 5 találkozásnak megfelelően a megfelelő madárpályák páronként metszik egymást, hiszen bármelyik két útvonal metszéspontja fölött áthaladva a hozzájuk tartozó két madár magassága egyenlő volt (3. ábra).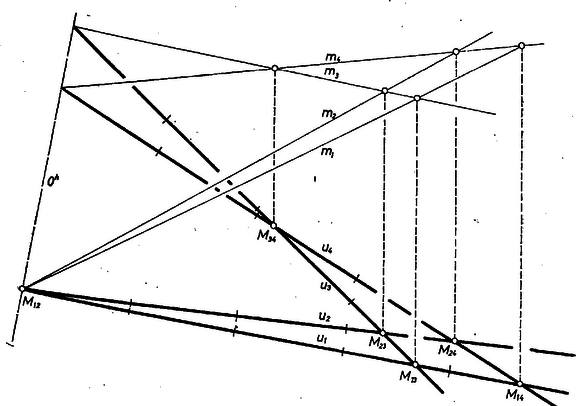

3. ábra

Mármost

m_{1}, m_{2}

és

m_{4}

egy síkban van, mert páronként metszik egymást, különböző pontokban. Ugyanígy

m_{1}, m_{3}

és

m_{4}

is egy síkban és ez a sík azonos az előbbivel, mert két különböző közös egyenesük van. Eszerint

m_{2}

és

m_{3}

egy síkban van, metszik egymást. A metszéspontban

J_{2}

és

J_{3}

madara találkozott, mert a metszéspont magassági értékét mindkettő egyszerre haladta át, ezért (alattuk) járműveik is éppen találkoztak.
Szamosújvári Sándor (Debrecen, KLTE Gyak. Gimn., III. o. t.)
ötlete, módosítva

IV. megoldás. Vegyünk fel a síkban egy tetszőleges pontot origónak, és jellemezzük a sík pontjait az origóból hozzájuk vezető vektorral, az illető pont helyvektorával. Ha egy egyenletesen mozgó jármű a

t_{1}

időpontban az

x_{1}

helyen,

t_{2}

időben pedig

x_{2}

-ben van, akkor a

t

időponthoz tartozó

x (t)

helyvektor:

\begin{matrix} x (t) = \frac{(t_{2} - t) x_{1} + (t - t_{1}) x_{2}}{t_{2} - t_{1}}, \end{matrix}

(1)

hiszen a jármű sebessége

\frac{x_{2} - x_{1}}{t_{2} - t_{1}}

, így az

x_{1}

pontból indulva

t - t_{1}

idő múlva az

\begin{matrix} x (t) = x_{1} + (t - t_{1}) \frac{x_{2} - x_{1}}{t_{2} - t_{1}} \end{matrix}

pontba jut, amiből egyszerű átalakítással kapjuk (1)-et.
Jelöljük az

M_{12}, M_{14}, M_{34}

pontok helyvektorát rendre

a, b, c

-vel, az

M_{13}, M_{24}

pontokét

c_{1}

a_{1}

-gyel. Ekkor (1) alapján

\begin{matrix} c_{1} = \frac{60 a + 220 b}{280}, a_{1} = \frac{110 b + 40 c}{150} . \end{matrix}

Hasonló eredményt kapunk, ha az

a, b, c

helyvektorú pontokban rendre 60, 220, 80 egységnyi tömeget helyezünk el: ekkor

c_{1}

épp az

a, b

tömegpár súlypontja,

a_{1}

pedig a

b, c

tömegpáré.
A három tömeg (együttes) súlypontja:

\begin{matrix} s = \frac{60 a + 220 b + 80 c}{360} . \end{matrix}

Ez a pont rajta van a II., III. jármű útvonalán, vagyis az

{a, a}_{1}

, illetve

{c, c}_{1}

szakaszon, hiszen

\begin{matrix} s = \frac{60 a + 300 a_{1}}{360} = \frac{280 c_{1} + 80 c}{360} . \end{matrix}

(1) alapján meghatározhatjuk azt is, hogy a pálya egy adott

x

pontján milyen

t

időpontban halad át a jármű:

\begin{matrix} (t_{2} - t) : (t - t_{1}) = (x_{2} - x) : (x - x_{1}) . \end{matrix}

Eszerint a II. jármű az

s

ponton abban a

t_{II}

időpontban halad át, melyre (az időt

0^{h}

-tól percben mérve)

\begin{matrix} (240 - t_{II}) : t_{II} = 60 : 300 = 1 : 5, \end{matrix}

azaz

t_{II} = 200

. Hasonlóan a III. jármű

s

-en való áthaladásának

t_{III}

időpontjára.

\begin{matrix} (240 - t_{III}) : (t_{III} - 130) = 80 : 280 = 2 : 7, \end{matrix}

azaz

t_{III} = 200

, vagyis a két jármű valóban egy időben halad át

s

-en.
(Tusnády Gábor)

Megjegyzés. A fenti gondolatmenettel beláthatjuk, hogy ha a járművek az

a, b, c

pontokban

t_{1}, t_{2}, t_{3}

időpontban haladnak át, és az

s

pont az

a, b, c

-ben ható rendre

α, β, γ

nagyságú súlyokhoz tartozó súlypont, akkor a megfelelő járművek

s

-en a

\begin{matrix} t = \frac{α t_{1} + β t_{2} + γ t_{3}}{α + β + γ} \end{matrix}

időpontban haladnak át. Feladatunk adataival

\begin{matrix} t = \frac{60 \cdot 0 + 220 \cdot 280 + 80 \cdot 130}{360} = 200. \end{matrix}