Kezdőlap


Feladat:	F.1620	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Ágoston Péter , Takács Andor
Füzet:	1969/május, 198 - 199. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Síkgeometriai számítások trigonometria nélkül sokszögekben, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1968/szeptember: F.1620

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az $S = A B C D E F$ szabályos hatszögbe beírt $H = P Q R$ háromszögnek $P Q$ oldala az $A B$ oldallal párhuzamos úgy, hogy $P$ az $A F$ oldalon van, tehát $Q$ a $B C$ -n. Nyilvánvaló, hogy így akkor legnagyobb $H$ területe, ha $R$ a $D E$ oldalon van, továbbá $R$ -et a $D E$ oldalon mozgatva (és $P Q$ -t változatlanul hagyva) a terület nem változik. Ezért $R$ -et rögzíthetjük $D E$ felezőpontjában.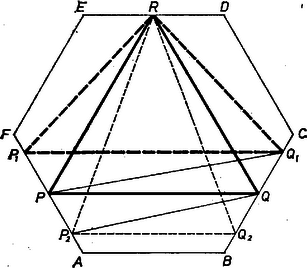
Megmutatjuk, hogy $H$ területe akkor a legnagyobb, ha $P$ felezi az $A F$ oldalt: $P A = P F$ . Legyen ekkor $P_{1}$ a $P F$ szakaszon, és messe a rajta átmenő, $A B$ -vel párhuzamos egyenes $B C$ -t $Q_{1}$ -ben.

1. ábra

Ekkor, minden idom területét ugyanúgy jelölve, mint magát az idomot (1. ábra):

\begin{matrix} H_{1} = P_{1} Q_{1} R = P Q R + P P_{1} R + Q Q_{1} R - Q Q_{1} P - P P_{1} Q_{1} = \\ = P Q R - (P P_{1} Q_{1} - P P_{1} R) < P Q R = H, \end{matrix}

hiszen a feltevés miatt

P R | | B C

és emiatt

Q Q_{1} R - Q Q_{1} P = 0

, másrészt

R Q | | A F

és

Q_{1}

Q C

szakaszon van, tehát messzebb van

P P_{1}

-től, mint

Q

és

R

, és így a zárójelbeli különbség pozitív, a kivonandó elhagyásával a kifejezést növeltük.
Hasonlóan ha

P_{2}

P A

szakaszon van és

P_{2} Q_{2} | | A B

, akkor

Q_{2}

B Q

-n adódik és

\begin{matrix} H_{2} = P_{2} Q_{2} R = P Q R + P P_{2} Q + Q Q_{2} P_{2} - P P_{2} R - Q Q_{2} R = P Q R - \\ - (P P_{2} R - P P_{2} Q) - (Q Q_{2} R - Q Q_{2} P_{2}) < P Q R = H, \end{matrix}

mert az első zárójel 0, a második pozitív, hiszen

P_{2}

közelebb van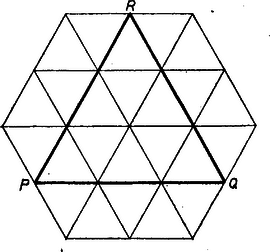

B C

-hez, mint

R

és

P

2. ábra

Ezek szerint az előírt tulajdonságú, legnagyobb területű

H

háromszög az

S

-nek

9 / 24 = 3 / 8

részét teszi ki (2. ábra), ez a vizsgálandó arány legnagyobb értéke.
Ágoston Péter (Budapest, Berzsenyi D. Gimn., II. o. t.)

II. megoldás. Legyen

P Q

távolsága

A B

-től

x (\leq A E / 2 = A B \sqrt[]{3} / 2)

, é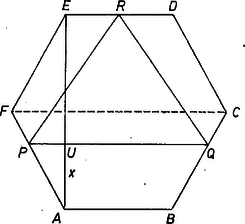s messe

P Q

A E

-t

U

-ban (3. ábra).

3. ábra

Ekkor a szimmetriára tekintettel

\begin{matrix} P Q R = \frac{1}{2} P Q \cdot U E = \end{matrix}

\begin{matrix} = \frac{1}{2} (A B + 2 P U) (A E - A U) = \\ = \frac{1}{2} (A B + \frac{2}{\sqrt[]{3}} x) (A B \sqrt[]{3} - x) = \\ = \frac{1}{\sqrt[]{3}} (\frac{A B \sqrt[]{3}}{2} + x) (A B \sqrt[]{3} - x) . \end{matrix}

A változó tényezők összege állandó, így ‐ mint ismeretes ‐ szorzatuk akkor a legnagyobb, ha a két tényező egyenlő, amiből

\begin{matrix} x = \frac{A B \sqrt[]{3}}{4} = \frac{A E}{4}, \end{matrix}

vagyis

P Q

felezi

A B

és

F C

távolságát:

P A = P F

Takács Andor (Csurgó, Csokonai Vitéz M. Gimn., IV. o. t.)