Kezdőlap


Feladat:	F.1618	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Balogh Zoltán , Galántai Aurél , Máté András
Füzet:	1970/március, 100 - 102. oldal		PDF \| MathML
Témakör(ök):	Exponenciális egyenlőtlenségek, Logaritmusos egyenlőtlenségek, Természetes számok, Szorzat, hatvány számjegyei, Feladat
Hivatkozás(ok):	Feladatok: 1968/szeptember: F.1618

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. A $61$ számjegyről szóló adat felhasználásával alsó és felső korlátot kapunk a keresett $N$ szám $10$ -es alapú logaritmusára. Legyen lg $N$ karakterisztikája $k$ (nyilván $k ≧ 0$ ), mantisszája $m$ . Eszerint

\begin{matrix} 10^{k} ≦ N < 10^{k + 1} \end{matrix}

és

n ≧ 0

esetén

\begin{matrix} 10^{n k} ≦ N^{n} < 10^{n (k + 1)}, \end{matrix}

tehát

N^{n}

számjegyeinek

j_{n}

számára fennáll

\begin{matrix} n k + 1 ≦ j n ≦ n (k + 1), \end{matrix}

hiszen a

10^{a}

hatvány

a + 1

jegyű, ha

a

természetes szám, vagy

0

. Ezt felírva az

n = 1

2, ...,6

értékekre és az egyenlőtlenségeket összeadva

\begin{matrix} (1 + 2 + ... + 6) k + 6 = 21 k + 6 ≦ j_{1} + j_{2} + ... + j_{6} ≦ 21 (k + 1), \end{matrix}

vagyis esetünkben

\begin{matrix} 21 k + 6 ≦ 61 ≦ 21 (k + 1), \end{matrix}

(1)

amiből

\begin{matrix} k = 2, \end{matrix}

tehát

N

háromjegyű szám,

100 ≦ N ≦ 999

.
A háromjegyű számokon végigmenve

N^{2}, N^{3}, ..., N^{6}

számjegyeinek száma akkor ugrik 1-et‐l-et, amikor

m

átlépi az

1 / 2

, i11. az

1 / 3

és a

2 / 3, ...

, ill. az

1 / 6

2 / 6, ...,5 / 6

értéket, mert így

2

-szerese,

3

-szorosa,

...

6

-szorosa 1‐1 újabb egész számot ad a hatvány karakterisztikájának növeléséhez. Esetünkben célszerűbb a háromjegyű számokon

999

-től visszafelé haladni, mert az előírt

61

számjegy csak

2

-vel kisebb az (1) szerint legnagyobb lehetséges

63

-nál, amit a

999

feltehetően el is ér. Keressük ki ezért a mondott átlépési értékek közül a legnagyobb hármat:

5 / 6

4 / 5

3 / 4

, állítjuk, hogy

m

az utóbbi kettő közé esik:

\begin{matrix} \frac{3}{4} ≦ m < \frac{4}{5} . \end{matrix}

Így ugyanis többszöröseinek egész része rendre

\begin{matrix} [m] = 0, [2 m] = 1, [3 m] = 2, [4 m] = 3, [5 m] = 3, [6 m] = 4, \end{matrix}

ezért

N^{n}

karakterisztikája rendre

\begin{matrix} 1 \cdot 2 + 0 = 2, 2 \cdot 2 + 1 = 5, 3 \cdot 2 + 2 = 8, 4 \cdot 2 + 3 = 11, 5 \cdot 2 + 3 = 13, 6 \cdot 2 + 4 = 16, \end{matrix}

(2)

és

N^{n}

jegyeinek száma rendre

\begin{matrix} 3, 6, 9, 12, 14, 17, \end{matrix}

összegük

61

. Mindezek szerint, tizedes törtekre áttérve

\begin{matrix} 2, 75 ≦ lg N < 2, 80, & (3) \\ 562 < N < 632. \end{matrix}

(Az iskolai függvénytáblázat szerint, 4 tizedesjegyre kerekítve

lg 631 = 2, 8000

, tehát

631

is szóba jöhet, amennyiben ez az érték fölfelé van kerekítve.)
II. Tovább a hatványok kezdő jegyének

24

-es összege alapján haladunk. A (3) intervallumbeli számokon végigmenve hatványaik nőnek, de jegyeik száma már nem nőhet, ezért a kezdő jegyek ‐ hatványkitevőnként külön-külön ‐ (tágabb értelemben) monoton növekednek. Célszerű ezért próbát tenni a (3)-ba eső és könnyen számítható 600 esetével. Kezdő jegyei egyeznek 6 hatványainak (

6

36

216

1296

7776

46 656

) kezdő jegyeivel, ezek összege 23, tehát

N > 600

, és

N

-et tovább növelve csak egyetlen hatvány kezdő jegye növekedhet 1-gyel a még fennálló 24‐23 hiány pótlására.

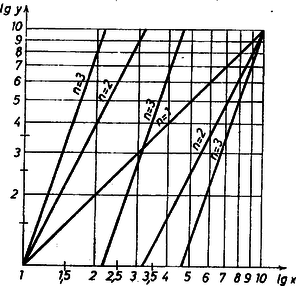1. ábra

Szemügyre véve e hatványok második jegyét,

N^{5}

és

N^{6}

-nál várható, hogy kezdő jegye leghamarabb éri el a 8-at, majd a 9-et, ill. az 5-öt. (Arra is gondoltunk, hogy nagyobb kitevő esetén a növekedés gyorsabb.) Ezért kiszámítjuk ‐ (2) figyelembevételével ‐ a

8 \cdot 10^{13}

és

9 \cdot 10^{13}

átlépési helyek ötödik gyökét és

5 \cdot 10^{16}

-nak hatodik gyökét. Ezek (logaritmusukból, ami rendre

2, 7806

2, 7908

, ill.

2, 7832

\begin{matrix} 603, 4, 617, 7, 606, 9, \end{matrix}

tehát a kezdő jegyek összege 604 esetében ugrik 24-re és 607-nél már 25. Ezek között egyetlen páratlan számként

N = 605

jön szóba. Valóban, normálalakban

\begin{matrix} 605^{2} = 3, 66 \cdot 10^{5}, 605^{3} = 2, 21 \cdot 10^{8}, 605^{4} = 1, 34 \cdot 10^{11}, \\ 605^{5} = 8, 10 \cdot 10^{13}, 605^{6} = 4, 90 \cdot 10^{16}, \end{matrix}

és itt a kezdő számjegyek különbözők, tehát a keresett szám valóban 605. (A kezdő jegyek különbözőségének követelményét csak ellenőrzésül használtuk fel.)

Galántai Aurél (Budapest, Bem J. Ip. Szakközépisk., IV.o. t.),

Máté András (Budapest, I. István Gimn., II. o. t.) és

Balogi Zoltán (Debrecen, Fazekas M. Gimn., I. o. t.)

dolgozatai alapján, kiegészítésekkel

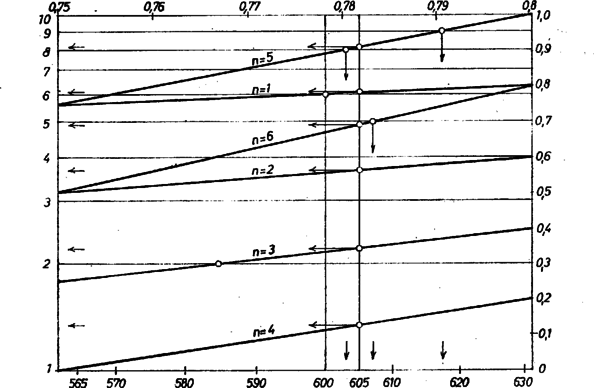2. ábra

Megjegyzés. A kitűzésben ajánlott ábrázolás azért egyszerű, mert az

y = x^{n}

függvény képe az ajánlott, ún. kétszer logaritmikus függvény-papíron egyenes vonal, hiszen

lg y = n \cdot lg x

. Az 1. ábráról

1 ≦ x ≦ 10

és

n = 1,2,3

esetére

x^{n}

kezdő számjegye olvasható le. A 2. ábra más léptékben a (3) intervallumra adja meg ezeket mind a 6 kitevőre, így más úton végezhetjük el a megoldásbeli próbákat.