Kezdőlap


Feladat:	1616. matematika feladat	Korcsoport: 16-17	Nehézségi fok: -
Megoldó(k):	Bálványos Z. , Bárány S. , Draschitz Rudolf , Gulyás A. , Göndöcs F. , Hárs L. , Jankó B. , Katona V. , Koren A. , Lempert L. , Maróti Péter , Máthé Mariann , Nagy András , Nagy Dénes , Nagy Zsigmond , Pál J. , Pintér Ágnes , Sax Gy. , Szabó Zsolt , Zambó Péter
Füzet:	1971/február, 50 - 52. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenletek, Vetítések, Háromszög alapú hasábok, Feladat
Hivatkozás(ok):	Feladatok: 1968/május: 1616. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Legyen a metszet $A$ csúcsának merőleges vetülete a $B$ -t tartalmazó oldalélen $A_{1}$ , ugyanígy $B$ és $C$ vetülete a $C$ -t, ill. $A$ -t tartalmazó oldalélen 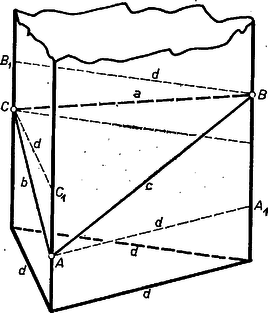$B_{1}$ , ill. $C_{1}$ .

Így

A A_{1} = B B_{1} = C C_{1} = d

, és az

A B C

háromszög csúcsainak magasságkülönbsége (a hasáb alapháromszögét vízszintes síkra téve) az

A B A_{1}

B C B_{1}

C A C_{1}

derékszögű háromszögekből rendre

\begin{matrix} A_{1} B = \sqrt[]{c^{2} - d^{2}}, B_{1} C = \sqrt[]{a^{2} - d^{2}}, C_{1} A = \sqrt[]{b^{2} - d^{2}} . \end{matrix}

(1)

a

b

c

szakaszhosszak egyenértékű szerepet játszanak a feladatban, ezért föltehetjük, hogy nagyságviszonyuk:

\begin{matrix} a ≦ b ≦ c, \end{matrix}

ezért

\begin{matrix} A_{1} B ≧ C_{1} A ≧ B_{1} C, \end{matrix}

és ebből

\begin{matrix} A_{1} B = C_{1} A + B_{1} C, \\ \sqrt[]{c^{2} - d^{2}} = \sqrt[]{b^{2} - d^{2}} + \sqrt[]{a^{2} - d^{2}}, \end{matrix}

hiszen a legnagyobb magasságkülönbség egyenlő a másik kettő összegével, az

A C B

törött vonaldarabon két lépésben ugyanannyit emelkedünk, mint a két végpontját összekötő egyenes szakaszon. Négyzetreemeléssel, átrendezéssel, újabb négyzetreemeléssel, végül

0

-ra redukálva az egyenletet:

\begin{matrix} c^{2} - d^{2} = a^{2} + b^{2} - 2 d^{2} + 2 \sqrt[]{(a^{2} - d^{2}) (b^{2} - d^{2})}, \\ d^{2} + c^{2} - a^{2} - b^{2} = 2 \sqrt[]{(a^{2} - d^{2}) (b^{2} - d^{2})}, \\ d^{4} + 2 (c^{2} - a^{2} - b^{2}) d^{2} + {(c^{2} - a^{2} - b^{2})}^{2} = 4 a^{2} b^{2} - 4 (a^{2} + b^{2}) d^{2} + 4 d^{4}, \\ 3 d^{4} - 2 (a^{2} + b^{2} + c^{2}) d^{2} + {4 a^{2} b^{2} - {(c^{2} - a^{2} - b^{2})}^{2}} = 0, & (2) \end{matrix}

ami

d^{2}

-re másodfokú egyenlet.
A diszkrimináns

1 / 4

része így alakítható:

\begin{matrix} D & = {(a^{2} + b^{2} + c^{2})}^{2} - 12 a^{2} b^{2} + 3 {(c^{2} - a^{2} - b^{2})}^{2} = \\ = 4 (a^{4} + b^{4} + c^{4} - a^{2} b^{2} - a^{2} c^{2} - b^{2} c^{2}) = \\ = {(a^{2} + c^{2} - 2 b^{2})}^{2} + 3 {(c^{2} - a^{2})}^{2} ≧ 0, & (3) \end{matrix}

tehát a

d^{2}

-re adódó értékek valósak (az utolsó lépésben az idézett megoldás egyik átalakítását fordított irányban alkalmaztuk).
Könnyű megmutatni másrészt az

U^{2} - V^{2} = (U - V) (U + V)

szorzattá alakítás háromszori alkalmazásával, hogy az egyenlet

d

-t nem tartalmazó tagja egyenlő az

A B C

háromszög területe

4

-szeresének négyzetével, tehát pozitív szám.

d^{2}

együtthatója viszont negatív (és

d^{4}

együtthatója pozitív), vagyis a két (valós)

d^{2}

gyöknek a szorzata is, összege is pozitív, tehát mindkettő pozitív.

A (2) gyökei csak

D = 0

esetén egyenlők, és ez csak akkor áll be, ha (3)-nak mindkét tagja

0

, azaz

c^{2} = a^{2}

, és így az első tagból

a^{2} = b^{2}

, vagyis ha

a = b = c

. Ekkor, mint könnyen látható,

d

is egyenlő velük.
Ha viszont

a

b

és

c

nem mind egyenlők, akkor

D > 0

, és a

d^{2}

-re adódó nagyobbik érték nagyobb

a^{2}

-nél, tehát (1) szerint feladatunk szempontjából nem használható, eszerint a szabályos háromszög alapidom keresett oldalhosszára nézve egyértelműen

\begin{matrix} d^{2} = \frac{1}{3} {a^{2} + b^{2} + c^{2} - 2 \sqrt[]{a^{4} + b^{4} + c^{4} - a^{2} b^{2} - a^{2} c^{2} - b^{2} c^{2}}} . \end{matrix}

(4)

II. Az 1527. feladatban az egyenes hasáb alapháromszögének oldalai voltak

a

b

c

, és a hasáb szabályos háromszög alakú (ferde) metszetének

d

oldalára kapott eredmény (4)-től csak a négyzetgyök előjelében tér el. Eszerint az a

d

érték ‐ bár kissé más összefüggésekből kaptuk ‐ számértékben egyenlő (2)-nek a nagyobbik gyökével.

Draschitz Rudolf (Budapest, Landler J. Gépip. Techn.)

Nagy Zsigmond (Budapest, Kaffka M. Gimn.)