|
| Feladat: |
1607. matematika feladat |
Korcsoport: 18- |
Nehézségi fok: nehéz |
| Megoldó(k): |
Bálványos Z. , Barna K. , Bertók P. , Draschitz R. , Győry Gy. , Hárs L. , Katona V. , Kóczy L. , Koren A. , Kovalszky Róbert , Lempert L. , Máthé Marianna , Nagy András (III. o.) , Nagy Dénes , Nagy Zsigmond , Sax Gy. , Szilágyi Etelka , Sztrapkovics L. , Váli L. , Waszlavik L. , Zambó Péter , Zöldy B. |
| Füzet: |
1969/január,
12 - 16. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Szinusztétel alkalmazása, Szabályos sokszögek szerkesztése, Feladat |
| Hivatkozás(ok): | Feladatok: 1968/április: 1607. matematika feladat |
|
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Jelöljük a keresett ötszögnek az adott , , , pontokon átmenő oldalegyeneseit, ill. a ponton átmenő átlójának egyenesét rendre , , , ill. betűvel. A , , egyenesek egyenlő szárú háromszöget határoznak meg, melynek -n van az alapja, és az ezen fekvő szögei -osak; az egyenes pedig párhuzamos -vel. Elegendő ezt a négy egyenest meghatároznunk, hiszen a keresett ötszöget egyértelműen meghatározzák: a , , egyenesek metszéspontjai az ötszög 3 csúcsát adják, az ezeken átmenő kör pedig az egyenesből kimetszi a hátra levő két csúcsot.
Legyen a , egyenesek metszéspontja . Elegendő ezt meghatároznunk, hiszen , megadja a , egyenest, az általuk meghatározott szögek közül a kisebbiket felező egyenes megadja és állását, tehát e szögfelezővel -n, -n át húzott párhuzamos adja az , ill. egyenest.
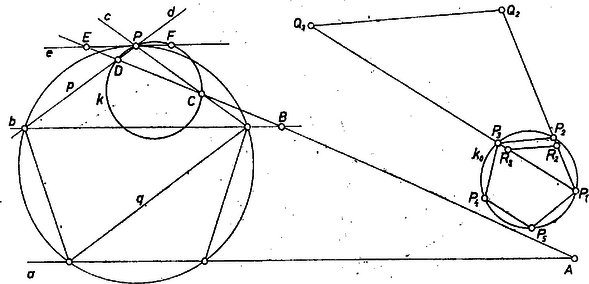 1. ábra
Húzzunk párhuzamost -n át -vel, jelöljük a kapott egyenest -vel, az adott szelővel alkotott metszéspontját -vel. A egyenesnek és közti szakasza egyenlő az ötszög oldalával, a és egyenesek közti szakasza pedig egyenlő az ötszög -vel párhuzamosan haladó átlójával. A párhuzamos szelők tétele alapján A arány tetszőleges szabályos ötszögben meghatározható, az szakaszhoz tehát megszerkeszthetjük a szakaszt, az egyenesen így kijelölhetjük az pontot.
-ből a szakasz -os vagy -os szög alatt látszik. A megfelelő négy látókörív alkalmas párokba kapcsolva két, a egyenesre nézve szimmetrikusan elhelyezkedő kört alkot. Elegendő közülük az egyiket felvennünk, ugyanis a belőle származtatott megoldást az egyenesre tükrözve a másikból levezethető megoldást kapjuk. Legyen ez a kör . Mivel a , egyenesek által meghatározott szögek közül a kisebbiket felezi, egyszersmind -nak a húrhoz tartozó ívei közül a rövidebbet is felezi.
Adataink alapján a kör és az ennek rövidebb ívét felező pont meghatározható, és ekkor az egyenes kimetszi -ból a keresett pontot. Ezek szerint a szerkesztés a következő.
Tetszőleges körbe (az ismert módon) szabályos ötszöget szerkesztünk, legyen ennek három, egymás utáni csúcsa , , . -ből irányában felmérjük a szakaszt. -on át párhuzamost húzunk -mal, ez a egyenest -ben metszi. Ekkor a szakaszt az szakasz -n túli meghosszabbítására felmérve kapjuk -t.
Mérjük fel -ből felé a szakaszt és messük az -on átmenő, -mal párhuzamosan húzott egyenessel -t -ben. A szakasz fölé a háromszöggel egybevágó háromszöget szerkesztünk, ennek harmadik csúcsa . A háromszög köré írt kört az egyenes másodszor a pontban metszi. ismeretében a keresett ötszög a fent előre leírt módon határozható meg.
A szerkesztés mindig végrehajtható. Megemlítjük, hogy ha a ponttal azonosnak adódik, akkor a egyenest nem határozzák meg a , pontok, így -t a egyenesnek -re vonatkozó tükörképeként kell előállítanunk. Ekkor az adott szelő az ötszög egyik oldalegyenese. (A szelőnek bármely a utáni pontjából kiindulva ugyanaz az ötszög adódik.) Hasonló a helyzet, ha a -vel adódik azonosnak.
Megmutatjuk, hogy a kapott ötszög valóban szabályos. Mivel felezi -nak a , egyenesek közti rövidebb ívét, felezi a , egyenesek által meghatározott kisebbik szöget. -t -vel párhuzamosnak szerkesztettük, a , , egyenesek tehát egyenlő szárú háromszöget határoznak meg, amelynek alapja -n van és az alapján levő szögek -osak (egyenlők a , közti kisebbik szög, a felével). A köré írható körbe írt, csúcsú szabályos ötszög -vel szomszédos csúcsai tehát azonosak megfelelő csúcsaival. Az ötszög -vel szemközti oldalának -től mért távolsága úgy aránylik -nek -től mért távolságához, mint az ötszög átlója az oldalához, tehát mint a szakaszhoz. Eszerint (1) miatt az egyenes azonos -val, a kapott ötszög valóban szabályos.
II. megoldás. A feladat megfordításaként először egy alkalmas szabályos ötszöghöz olyan szelő egyenest szerkesztünk, melyen a megfelelő oldal-, ill. átlóegyenesek által kimetszett, egymás utáni , , , pontok közti szakaszok aránya megegyezik az adott szelőn levő szakaszok arányával: Azután ezen ötszög és szelő együttes alakzatát úgy fordítjuk el és nagyítjuk vagy kicsinyítjük, hogy , , , megfelelője rendre az adott , , , ill. pontba essék.
Olyan szabályos ötszögből indulunk ki, melyben a oldal és a vele párhuzamos átló távolsága kisebb az szakasznál (2. ábra).
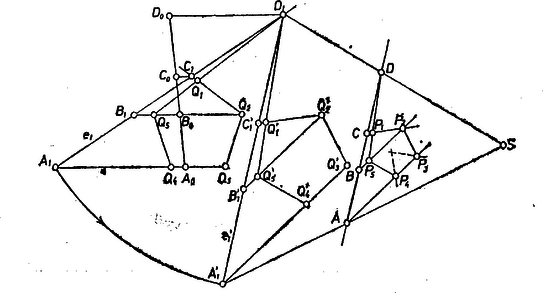 2. ábra
Legyen tetszés szerinti pontja , az körüli, sugarú körnek -ön levő pontja , és az félegyenesen az a pont, amelyre , . Húzzunk párhuzamost -gyel -on és -on át, és messe ez a , ill. egyenest a , ill. pontban, végül legyen a egyenesnek -en levő pontja , -ön levő pontja . Ekkor nyilvánvalóan | |
tehát a keresett szelő a egyenes.
Fordítsuk el és alakzatát körül úgy, hogy a félegyenes a félegyenessel párhuzamos és egyirányú helyzetbe jusson, és legyen ekkor , , valamint új helyzete , , ill. , továbbá és metszéspontja . Így a fentiek szerint és ugyancsak átmennek -en, tehát , , , rendre az , , , pont képe egy középpontú, alkalmas arányú hasonlósági transzformációban, ezért a keresett ötszög , , , oldal‐, ill. átlóegyenese rendre az -n, -n, -n, -n át, rendre -vel, -vel, -vel, ill. -vel párhuzamosan húzott egyenes lesz. Ezek alkalmas párjainak metszéspontja adja -et, -t, -öt, végül -at, -et az -n át -vel húzott párhuzamosból , ill. felező merőlegese metszi ki.
A szerkesztés a fentiek szerint egyértelműen végrehajtható. Ha azonban (vagy ) éppen -be esik, akkor -ként a (ill. ) oldalegyenes adódik, és nem egyedüli közös pontja -nek és -nek. Ez a kapcsolat természetesen megmarad az elfordítással és nagyítással kapott ötszög és az adott között is.
A szerkesztés helyességének bizonyítását az olvasóra hagyjuk.
Kovalszky Róbert (Budapest, Landler J. Gimn.) dolgozatának felhasználásával
Megjegyzés. A megoldás első részében lényegében az szelő és a egyenes közti szöget szerkesztettük meg. Ezt számítással készíti elő a következő megoldás.
III. megoldás (vázlat). A fentebbi jelöléseket tovább használva és a egyenes közti szöget szerkesztjük meg arra a helyzetre, amikor a oldalszakaszra jut, pedig a oldal meghosszabbítására (3. ábra), számítással előkészítve és ezen korlátozása folytán a szakaszon van, és .
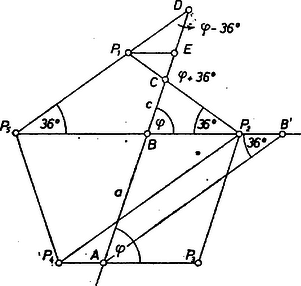 3. ábra
Legyen , , , és messe -öt az -n átmenő, -gyel párhuzamos egyenes -ben. , , így a színusz tételt alkalmazva rendre a , , háromszögre:
Ezeket a egyenlőségbe helyettesítve és a közös nevezőt elhagyva
A szükségessé vált -os szöget egy előre megszerkesztett szabályos ötszög három egymás utáni , , csúcsával meghatározott egyenlő szárú háromszögből vesszük (4. ábra).
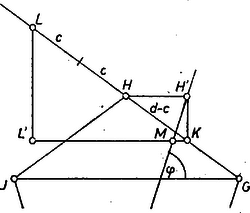 4. ábra
Felmérjük a szárra a , valamint -n túli meghosszabbítására a szakaszt, igy . -n át párhuzamost húzunk a alappal, valamint merőlegest rá; legyen vetülete az előbbin , és vetülete az utóbbin . Mérjük fel végül -től irányában az szakaszt, ekkor a szög adja -t, ill. kiegészítő szögét, amennyiben az meghosszabbításán adódott.
A szög ismeretében lényegében a II. megoldás befejező része szerint kaphatjuk meg az ötszöget.
Lényegében ugyanígy megy a számítás és a szerkesztés akkor is, ha , az 1. vagy a 2. ábra szerint helyezkednek el az ponthoz viszonyítva.
Megjegyzések. 1. Számításunk kapcsolatba hozható az I. megoldásban felhasznált ponttal. (2)-t alakítva | |
másrészt, mint ismeretes, ezért (1) alapján ennélfogva a számláló , Ezt pedig úgy is megkapjuk, ha a színusz tételt a háromszögre írjuk fel, alkalmazzuk a szögfelező osztásarányának tételét (hacsak ): | |
mindkét oldalból 1-et kivonva, ill. mindkettőhöz 1-et hozzáadva | |
végül ezek hányadosa azonos (3)-mal.
2. Az pontnak pl. -vel való egybeesése most már azt jelenti, hogy , így (2) számlálója , és ezért értékétől függetlenül .
Legtöbb versenyzőnk ezen az úton oldotta meg (vagy közelítette meg) a feladatot, és ugyanez volt a helyzet annak idején a tanulmányi versenyen is. |
|
 PDF |
PDF |  MathML
MathML 


