Feladat: 1605. matematika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Birkner Lajos ,  Hárs László ,  Katona Viktor ,  Kovalszky Róbert ,  Lempert László ,  Nagy Dénes ,  Papp Zoltán ,  Tél Tamás 
Füzet: 1970/május, 206 - 207. oldal  PDF  |  MathML 
Témakör(ök): Egyenesek egyenlete, Parabola egyenlete, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):Feladatok: 1968/április: 1605. matematika feladat

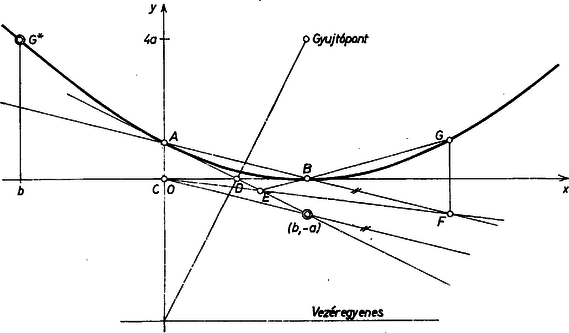
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Válasszuk koordináta-rendszerünk tengelyeinek a CB, CA egyeneseket és legyenek a koordináták A(0,a), B(b,0), így D(b/2,0), az AD egyenes tetszőleges pontja E(λb/2,(1-λ)a), ahol λ tetszőleges valós szám, a CE egyenes egyenlete pedig

y=2(1-λ)aλbx,
hacsak λ≠0, azaz ha E nem azonos A-val; ezt egyelőre feltesszük. Másrészt az AB egyenes egyenlete
x/b+y/a=1,
és így az F metszéspont abszcisszája
x0=λb/(2-λ),(1)
ha λ≠2. A λ=2 esetben E a (b,-a) pontban, A-nak D-re való tükörképében van, CE párhuzamos AB-vel, F nem jön létre és persze G sem.
A BE egyenes egyenlete
y=2(1-λ)ab(λ-2)(x-b),
és a szerkesztés szerint G ennek az (1) abszcisszájú pontja, tehát ordinátája
y0=4a(1-λ2-λ)2,
és innen (1) alapján
λ=2x0/(x0+b)(x0≠-b)(1')
kiküszöbölésével G koordinátái között a következő összefüggés adódik:
y0=ab2(x0-b)2.(2)

Ez az összefüggés a fent kihagyott λ=0 esetben is érvényes, hiszen akkor E-n kívül F és G is A-ban adódik, és A koordinátáival teljesül (2). Azt kaptuk tehát, hogy az egyetlen (b,-a) pont kivételével az AD egyenes minden pontjához tartozik az előírás szerint szerkesztett G pont, és ennek koordinátáira mindig teljesül (2). Ez az összefüggés parabola egyenlete, melynek csúcsa a B pont, csúcsérintője a BC egyenes és a parabola egy pontja A. (Könnyű belátni azt is, hogy a parabola fókusza a B-ben BC-re és D-ben DA-ra emelt merőlegesek metszéspontja.)
 

 

Fordítva, meg kell vizsgálnunk, hogy a (2) parabola mely pontjai tartoznak hozzá a keresett mértani helyhez. Legyen G(x0,y0) olyan pont, melyre teljesül (2). Ez csak az (1')-bó1 adódó λ-értékhez tartozó E pontból származhat, és E-ből a fentiek szerint valóban visszakapjuk G-t, hacsak x0≠-b, hiszen (1') értéke nem lehet 2. A parabolának tehát csak az x0=-b abszcisszán levő G*(-b,4a) pontja nem tartozik hozzá a keresett mértani helyhez, más szóval: a mértani helyet a (2) parabolából úgy kapjuk, hogy elhagyjuk belőle a G* pontot.
 

Megjegyzés. Megoldható a feladat a projektív geometria * tételei alapján is.
*Lásd pl.:Vigassy Lajos: Geometriai transzformációk, Középiskolai Szakköri Füzetek, Tankönyvkiadó, Budapest, 1963.