Kezdőlap


Feladat:	1604. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Gegesy F. , Hárs László , Hegedűs A. , Jánossy D. , Koren A. , Kovalszky R. , Lempert L. , Michaletzky Gy. , Nagy A. , Nagy D. , Nagy Zs. , Papp Z. , Pető J. , Sax Gy. , Tél T. , Viszeki Gy.
Füzet:	1969/február, 57 - 59. oldal		PDF \| MathML
Témakör(ök):	Diszkusszió, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1968/április: 1604. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Az $A_{1}$ talppontnak az $A_{2}$ felezőpontra vett tükörképe a háromszög $A$ csúcsa, a további két csúcs pedig az $A_{1}$ -ben $A_{1} A_{2}$ -re állított merőlegesen, az $a$ oldalegyenesen lesz ( $1$ . ábr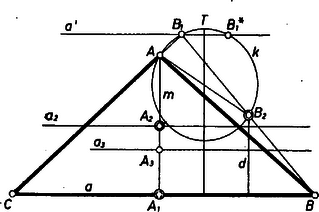a).

1. ábra

Az eddigiek alapján két mértani helyet kapunk a

B

-ből húzott magasság

B_{1}

talppontja számára. Egyrészt rajta lesz az

A B_{2}

szakasz fölötti

k

Thalész körön, másrészt ‐ mint a

B

csúcs

B_{2}

-re való tükörképe ‐ rajta lesz az

a

egyenes

B_{2}

-re való

a'

tükörképén; ezek szerint

B_{1}

k

és

a'

vonalak közös pontja. (Megjegyezzük, hogy nem lehet

B_{1}

B_{2}

-vel azonos, hiszen

B_{1}

B

-ből induló magasságszakasz másik végpontja,

B_{2}

pedig e szakasz felezőpontja.) Végül a

B

csúcs

B_{1}

-nek

B_{2}

-re vonatkozó tükörképe lesz,

C

-t pedig a

B_{2} B_{1}

egyenesre

B_{1}

-ben emelt merőleges

b

egyenes metszi ki

a

-ból.
A szerkeszthetőség feltétele tehát, hogy

k

-nak és

a'

-nek legyen

B_{2}

-től különböző metszéspontja, és a

b

egyenes messe

a

-t. Ha a szerkesztés végrehajtható, a kapott háromszög megfelel a feladat követelményeinek, hiszen

A

és

a

szerkesztése miatt

A_{1}

és

A_{2}

valóban az

A

-ból induló magasságszakasz végpontja és felezőpontja; a

b

egyenes átmegy az

A

csúcson Thalész tétele miatt, tehát oldalegyenese a kapott háromszögnek, így

B B_{1}

magasságszakasz, és

B_{2}

ennek felezőpontja.
Általában annyi megoldása van a feladatnak, ahány közös pontja van

k

-nak és

a'

-nek. Kivételt képez azonban az az eset, amikor az egyik közös pont azonos

B_{2}

-vel, mert

a'

átmegy

B_{2}

-n. Ez csak úgy adódhat, ha már

a

is átmegy

B_{2}

-n. Ha tehát

B_{2}

a

egyenes

A_{1}

-től különböző pontja, vagyis a

B_{2} A_{1} A_{2}

szög derékszög, akkor

1

megoldás van; ha pedig

B_{2}

és

A_{1}

azonos, akkor nincs megoldás.
További kivételes eset, ha

b

párhuzamosnak adódik

a

-val, tehát azonos az

a

-val párhuzamos,

A

-n átmenő egyenessel. Ez csak úgy adódhat, ha

B_{2}

A_{2}

-n átmenő,

a

-val párhuzamos

a_{2}

egyenesen van. Ha tehát

B_{2}

a_{2}

egyenes

A_{2}

-től különböző pontja, vagyis a

B_{2} A_{2} A_{1}

szög derékszög, akkor

1

megoldás van; ha pedig

B_{2}

azonos

A_{2}

-vel, akkor nincs megoldás.
A továbbiakban feltesszük, hogy

B_{2}

nincs rajta az

a

a_{2}

egyenesek egyikén sem. Legyen először

B_{2}

az a egyenesnek

A

-t tartalmazó oldalán. Ekkor a

k

kör

a

-tól legmesszebb levő

T

pontjának az

a

-tól mért távolsága

\begin{matrix} r + \frac{d + m}{2}, \end{matrix}

ahol

r

k

kör sugara,

d

és

m

B_{2}

, ill.

A

pont

a

-tól mért távolsága. Ekkor

k

és

a'

metszésének feltétele:

\begin{matrix} r + \frac{d + m}{2} \geq 2 d, (1) d - \frac{m}{3} \leq \frac{2}{3} r . \end{matrix}

Amennyiben itt egyenlőség teljesül, egy közös pont van, ha pedig az egyenlőtlenség teljesül, akkor kettő.
Ha

B_{2}

a

egyenes

A

-t nem tartalmazó oldalán van, akkor a metszés feltétele: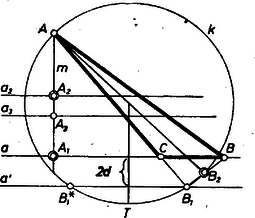

\begin{matrix} r - \frac{m - d}{2} \geq 2 d, d + \frac{m}{3} \leq \frac{2}{3} r . \end{matrix}

Eredményeink összefoglalása céljára húzzunk párhuzamost

a

-val az

A_{1} A

szakasz

A_{1}

-hez közelebbi

A_{3}

harmadoló pontján át, legyen ez

a_{3}

. Ha

B_{2}

-nek

A

-tól mért távolsága

r_{1}

(a fenti

2 r

), és

a_{3}

-tól mért távolsága

r_{2}

(a fenti jelöléssel

| d - \frac{m}{3} |

, ill.

d + \frac{m}{3})

, akkor

\begin{matrix} r_{2} & < r_{1} / 3 esetén két megoldás van, \\ r_{2} & = r_{1} / 3 esetén egy megoldás, \\ r_{2} & > r_{1} / 3 esetén pedig nincs megoldás . \end{matrix}

II. Az

r_{2} = r_{1} / 3

feltételnek eleget tevő pontok mértani helyét koordinátageometriai úton határozzuk meg. Legyen az

x

tengely az

a

egyenes, és az

y

tengely menjen át az

A

ponton. Ekkor a

B_{2}

(x, y)

pontra

\begin{matrix} r_{1}^{2} = x^{2} + {(y - m)}^{2}, r_{2}^{2} = {(y - \frac{m}{3})}^{2}, \end{matrix}

tehát az

r_{2} = \frac{1}{3} r_{1}

feltétel szerint

\begin{matrix} x^{2} + {(y - m)}^{2} = 3^{2} {(y - \frac{m}{3})}^{2}, \\ x^{2} + y^{2} - 2 y m + m^{2} = 9 y^{2} - 6 y m + m^{2}, \\ x^{2} - 8 y^{2} + 4 y m = 0, \\ - \frac{2 x^{2}}{m^{2}} + \frac{16 {(y - \frac{m}{4})}^{2}}{m^{2}} = 1. \end{matrix}

Ez hiperbola egyenlete, melynek valós tengelye az

A A_{1}

egyenes, csúcsai

A_{1}

és

A_{2}

, és egyik fókusza az

A

pont.
Mármost a hiperbola belsejében, valamint csúcspontjaiban felvett

B_{2}

esetén a megoldások száma

0

, a hiperbolára nézve külső pontokban

2

, kivéve az

a

a_{2}

egyeneseket ‐ vagyis a hiperbola csúcsérintőit ‐, valamint a két csúcs közti szakaszt, ahol

1

háromszög adódik, végül a hiperbola pontjaiban is

1

megoldás van (

2

. ábr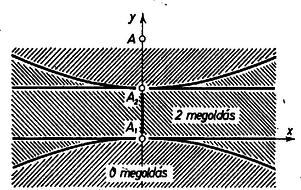a).

2. ábra

Hárs László (Budapest, Berzsenyi D. Gimn., III. o. t.)

Megjegyzés. A legutóbbiakban ezt is kaptuk: azoknak a pontoknak a mértani helye, amelyeknek egy adott ponttól (itt

A

-tól) és egy adott egyenestől (itt

a_{3}

-tól) mért távolságainak aránya

q = 3

, hiperbola.
Meg lehet mutatni, hogy ez bármely

q > 1

arányérték esetén érvényes,

0 < q < 1

esetén pedig ellipszis a mértani hely, továbbá hogy az adott pont minden esetben egyik fókusza lesz a kúpszeletnek, az adott egyenes merőleges a fókuszokat tartalmazó szimmetriatengelyre, a szokásos jelölésekkel

q = c / a

, és az egyenesnek a kúpszelet középpontjától mért távolsága

a^{2} / c