Kezdőlap


Feladat:	1600. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Barra Károly , Kemény András
Füzet:	1969/január, 10 - 12. oldal		PDF \| MathML
Témakör(ök):	Parabola, mint kúpszelet, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1968/március: 1600. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ismeretes, hogy az $F$ fókuszt tükrözve a parabola bármely $P$ pontjához tartozó $t$ érintőre, $P$ -nek a $d$ vezéregyenesen levő $V$ merőleges vetületét kapjuk, vagyis amely pontra a definíció szerint $P V = P F$ . Eszerint a szóban forgó $P'$ pont $V$ -nek képe a $t$ , $n$ egymásra merőleges egyeneseken való, egymás utáni két tükrözés után. Azt is tudjuk, hogy két ilyen tükrözés eredménye ugyanaz, mint a tengelyek metszéspontjára ‐ itt $P$ -re ‐ való tükrözésé, tehát $P'$ a $V P$ félegyenesen van, és 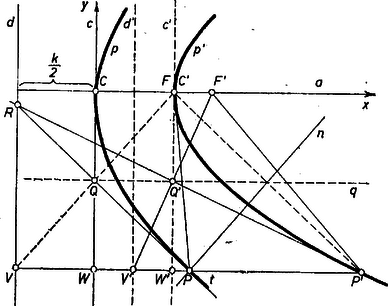$V P' = 2 \cdot V P$ .
Eszerint a keresett $p'$ mértani hely az adott $p$ parabolából áll elő, ennek a vezéregyenesére merőleges irányú $2 : 1$ arányú nyújtásával. Bebizonyítjuk, hogy $p'$ is parabola. Evégett megadunk egy olyan $F'$ pontot és $d'$ egyenest, melyektől $p'$ -nek minden pontja egyenlő távolságra van.

Ennek során felhasználjuk az ábra alakzatának alábbi két tulajdonságát.

F

-nek a fenti

t

érintőn levő

Q

vetülete rajta van

p

-nek

c

csúcsérintőjén, így a mondott tükrözés miatt

F Q = Q V

, eszerint

Q

rajta van az

a

parabolatengely és a

V P

egyenes közti síksáv

q

szimmetriatengelyén. Továbbá

c

és

V P

metszéspontját

W

-vel jelölve

F C Q

és

Q W P

hasonló derékszögű háromszögek, ezért

\begin{matrix} F C : C Q = Q W : W P = C Q : W P . \end{matrix}

(1)

Mármost

p

-nek

a

tengelye egyszersmind

p'

-nek is szimmetriatengelye, hiszen

F

-et

p

-nek két az

a

-ra szimmetrikus pontjához tartozó normálisra tükrözve a tükörképek szimmetrikus helyzetűek

a

-ra. Ha pedig

P

-ként

p

-nek

C

csúcsából indulunk ki,

P'

-ként

F

-et kapjuk, mert ekkor a normális azonos az

a

tengellyel, és

F

képe önmaga. Azt sejtjük tehát, hogy

p'

csúcsa

F

, és így az

F

-en átmenő,

a

-ra merőleges

c'

egyenes

p'

-nek csúcsérintője.
Legyen még

t

-nek

d

-vel való metszéspontja

R

, ekkor a megállapított nyújtásból azt is sejtjük, hogy az

R P'

egyenes

p'

-nek érintője. Ezek alapján várható, hogy

F'

-t és

d'

-t az alábbiak szerint kapjuk: messe

R P'

q

egyenest

Q'

-ben, ekkor a

Q'

-ben

R P'

-re állított merőleges

a

-ból

F'

-t, a

V P'

egyenesből pedig

d'

-nek egy

V'

pontját metszi ki, és így

d'

V'

-ből

a

-ra állított merőleges.
Ezt fogjuk bizonyítani. Így mindenesetre

Q' F' = Q' V'

, és így

P' F' = P' V'

P

egyenlő távolságra van

F'

-től és

d'

-től. Ezért csak azt kell belátnunk, hogy a szerkesztett

F'

pont és

d'

egyenes helyzete független

P

megválasztásától.

Q'

rajta van

c'

-n, mert

q ∥ V P'

és

V P' = 2 \cdot V P

miatt

q

-nak az

R V P'

háromszögbe eső szakaszát az

R P

súlyvonal felezi,

Q'

-nek

d

-től való távolsága 2-szer akkora, mint

Q

-é, egyszersmind

c

-nek

d

-től való távolsága. Legyen még

c'

és

V' P'

metszéspontja

W'

, ekkor

\begin{matrix} W' P' = V P' - V W' = 2 \cdot V P - 2 \cdot V W = 2 (V P - V W) = 2 W P, \end{matrix}

ezért az

F' C' Q'

és

Q' W' P'

hasonló derékszögű háromszögek, valamint (1) felhasználásával

\begin{matrix} F' C' = Q' W' \cdot \frac{C' Q'}{W' P'} = \frac{C Q^{2}}{W' P'} = \frac{C Q^{2}}{2 W P} = \frac{F C}{2} = állandó . \end{matrix}

Fordítva,

p'

-nek minden

P'

pontja előáll

p

-nek abból a

P

pontjából, amelyet a

P'

-n átmenő,

a

-val párhuzamos egyenes metsz ki.
Eszerint

p'

valóban parabola, csúcsa azonos

F

-fel, vezéregyenese pedig a

C F

szakasz felező merőlegese (paramétere fele akkora, mint az adott parabola paramétere).

Megjegyzés. A versenyzők a

V P' = 2 V P

összefüggés megállapítása után kizárólag koordináta-geometriai úton dolgoztak.
Legyen az adott parabola egyenlete

\begin{matrix} x = \frac{y^{2}}{2 k}, \end{matrix}

(2)

ennek vezéregyenese az

x = - k / 2

egyenes, így ha

P

koordinátái

(x, y)

, akkor

V P = x + k / 2

, és ezért

V P' = 2 V P = 2 x + k

és

P'

-nek

x'

y'

koordinátái:

\begin{matrix} x' = V P' - \frac{k}{2} = 2 x + \frac{k}{2}, y' = y . \end{matrix}

Innen

\begin{matrix} x = \frac{1}{2} (x' - \frac{k}{2}), y = y', \end{matrix}

és ezeket (2)-be helyettesítve

P'

-re a következő összefüggés áll fenn:

\begin{matrix} x' = \frac{y'^{2}}{k} + \frac{k}{2} . \end{matrix}

Ez pedig parabola egyenlete, melynek tengelye az

x

tengely (a pozitív fele), paramétere

k' = k / 2

és csúcsa a (

k / 2, 0

) pont, ennélfogva fókusza és vezéregyenese:

\begin{matrix} F' (\frac{3 k}{4}, 0), x = \frac{k}{4} . \end{matrix}

Kemény András (Budapest, Berzsenyi D. Gimn., II. o. t.)
Barra Károly (Salgótarján, Madách I. Gimn., IV. o. t.)