Kezdőlap


Feladat:	1598. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1968/november, 136 - 140. oldal		PDF \| MathML
Témakör(ök):	Kör egyenlete, Feladat
Hivatkozás(ok):	Feladatok: 1968/március: 1598. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. $m \neq 0$ miatt $v \neq 0$ , és így mindig fennáll $y \neq 0$ , másrészt $u \neq 0$ . A kifejezések mindig értelmezve vannak, mert közös nevezőjük nem kisebb, mint $v^{2}$ , ami pedig pozitív. (1) alapján

\begin{matrix} x + 1 = \frac{2 (1 - u)}{{(1 - u)}^{2} + v^{2}}, \end{matrix}

(3)

ezt (2)-vel osztva

\begin{matrix} \frac{x + 1}{y} = \frac{1 - u}{v} = \frac{1 - u}{m u}, \end{matrix}

és innen mindig

\begin{matrix} u = \frac{y}{y + m (x + 1)}, v = \frac{m y}{y + m (x + 1)}, \end{matrix}

(4)

ugyanis a nevező nem tűnik el, mert (2) és (3) alapján

\begin{matrix} y + m (x + 1) = \frac{2 m}{{(1 - u)}^{2} + v^{2}} \neq 0. \end{matrix}

Ezekre támaszkodva könnyen megkapjuk

x

y

és

m

kívánt alakú összefüggését. (4) alapján

\begin{matrix} 1 - u = \frac{m (x + 1)}{y + m (x + 1)}, \end{matrix}

és így (2)-nek

\begin{matrix} {(1 - u)}^{2} + v^{2} = \frac{2 v}{y} \end{matrix}

átrendezett alakjából:

\begin{matrix} \frac{m^{2} {(x + 1)}^{2}}{{[y + m (x + 1)]}^{2}} + \frac{m^{2} y^{2}}{{[y + m (x + 1)]}^{2}} = \frac{2 m}{y + m (x + 1)}, \\ {(x + 1)}^{2} + y^{2} = \frac{2}{m} [y + m (x + 1)], \\ x^{2} + {(y - \frac{1}{m})}^{2} = 1 + \frac{1}{m^{2}} . & (5) \end{matrix}

Ez kör egyenlete, melynek

K

középpontja és

r

sugara:

\begin{matrix} K (0, \frac{1}{m}), r = \sqrt[]{1 + \frac{1}{m^{2}}} . \end{matrix}

Kizártuk azonban az

y = 0

értéket, amelyhez (5) alapján

x = \pm 1

tartozik, ennélfogva a kérdéses vonal a mondott kör, az

x

tengelyen levő

(1,

0)

és

(- 1,

0)

metszéspontok kihagyásával (a körnek az

x

tengely fölötti és alatti íve).

Megjegyzések. 1. Megkaphatjuk (5)-öt a következő meggondolással is. A kérdéses vonal minden pontjához tartozik az

u

v

paramétereknek legalább egy, az előírások szerinti értékpárja, ill. a

v = m u

összefüggésnek és

m

állandó voltának figyelembevételével legalább egy

u

érték. Erre a pont mindkét koordinátája alapján

2 - 2

érték jön szóba, mert (1)-ből és (2)-ből

u

szerinti rendezéssel (ami a föltevések szerint ekvivalens átalakítás):

\begin{matrix} (1 + m^{2}) (x + 1) u^{2} - 2 x u + (x - 1) = 0, & (6) \\ (1 + m^{2}) y u^{2} - 2 (m + y) u + y = 0. & (7) \end{matrix}

Ez azt jelenti, hogy (6)-nak és (7)-nek van közös gyöke.
Várható, hogy ilyen esetben a két egyenlet együtthatói között összefüggés áll fenn, hiszen tetszés szerinti együtthatók esetén két másodfokú egyenlet

2 - 2

gyöke között nem várhatók egyenlők. Ezt az összefüggést keressük meg az,

\begin{matrix} a_{1} z^{2} + b_{1} z + c_{1} = 0, \\ a_{2} z^{2} + b_{2} z + c_{2} = 0 \end{matrix}

egyenlet-pár esetére, majd alkalmazzuk feladatunkra. Legyen közös gyökük

z_{1}

, ekkor fennáll

\begin{matrix} a_{1} z_{1}^{2} + b_{1} z_{1} + c_{1} = 0, & (8) \\ a_{2} z_{1}^{2} + b_{2} z_{1} + c_{2} = 0. & (9) \end{matrix}

Először

z_{1}^{2}

, majd

z_{1}

kiküszöbölésével (azaz (8)-at

- a_{2}

-vel, (9)-et

a_{1}

-gyel, majd

b_{2}

-vel, ill.

- b_{1}

-gyel szorozva és összeadva)

\begin{matrix} (a_{1} b_{2} - a_{2} b_{1}) z_{1} + (a_{1} c_{2} - a_{2} c_{1}) = 0, \\ (a_{1} b_{2} - a_{2} b_{1}) z_{1}^{2} + (c_{1} b_{2} - c_{2} b_{1}) = 0. \end{matrix}

Mármost az elsőből

\begin{matrix} {(a_{1} b_{2} - a_{2} b_{1})}^{2} z_{1}^{2} = {(a_{2} c_{1} - a_{1} c_{2})}^{2}, \end{matrix}

a másodikat

a_{1} b_{2} - a_{2} b_{1}

-gyel szorozva és a kapott összefüggést felhasználva:

\begin{matrix} {(a_{2} c_{1} - a_{1} c_{2})}^{2} + (a_{1} b_{2} - a_{2} b_{1}) (c_{1} b_{2} - c_{2} b_{1}) = 0. \end{matrix}

(10)

Ez a keresett összefüggés, közös gyökkel bíró két másodfokú egyenlet együtthatói között.
Esetünkben (6) és (7) együtthatóival (10) alapján:

\begin{matrix} 4 {(1 + m^{2})}^{2} y^{2} + 4 (1 + m^{2}) [y + m (x + 1)] [m (x - 1) - y] = 0, \end{matrix}

ami ismét (5)-re vezet.
2. Sejtést kaphatunk a kérdéses vonalra vonatkozóan néhány pontjának ábrázolásával is. Az 1. ábrán

m = 2

esetére az

u = \pm 0, 1

\pm 0, 2

\pm 0, 4

\pm 0, 6

\pm 0, 8

\pm 1

\pm 2

értékekkel kapott pontok kört rajzolnak ki.

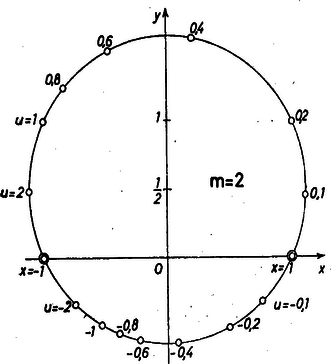1. ábra

II. megoldás. Az előző megoldás (3) és (2) formulájában a jobb oldalak számlálói a nevezőkben szereplő négyzetek alapjai. Így a két kifejezés négyzetét összeadva egyszerűsíteni lehet:

\begin{matrix} {(x + 1)}^{2} + y^{2} = \frac{4}{{(1 - u)}^{2} + v^{2}}, vagy \\ [{(x + 1)}^{2} + y^{2}] [{(1 - u)}^{2} + v^{2}] = 4. \end{matrix}

Ennek geometriai értelmet adhatunk, ha

u

-t,

v

-t is koordinátáknak fogjuk fel. A két tényező még szimmetrikusabbá válik, ha a

ξ = - u

η = v

koordinátákkal meghatározott

R

pontot tekintjük. Ehhez az

\begin{matrix} x = \frac{1 - ξ^{2} - η^{2}}{{(ξ + 1)}^{2} + η^{2}}, & (1^{*}) \\ y = \frac{2 η}{{(ξ + 1)}^{2} + η^{2}} & (2^{*}) \end{matrix}

összefüggés egy

P

(x

y)

pontot rendel, az

R_{0}

(- 1,

0)

pont kivételével, amire az

(1^{*})

(2^{*})

formuláknak nincs értelme. Fönt nyert összefüggésünk pedig az

\begin{matrix} [{(x + 1)}^{2} + y^{2}] [{(ξ + 1)}^{2} + η^{2}] = 4 \end{matrix}

alakot nyeri, amiből pontjaink távolságára az

\begin{matrix} R_{0} P \cdot R_{0} R = 2 \end{matrix}

(11)

összefüggés következik. A

(3)

és

(2^{*})

összefüggéseket

\begin{matrix} x + 1 = \frac{2}{R_{0} R^{2}} (ξ + 1), & (3^{*}) \\ y = \frac{2}{R_{0} R^{2}} η & (2^{*}) \end{matrix}

alakban írhatjuk, vagyis

x + 1

y

, a

ξ + 1

-ből, ill.

η

-ból ugyanazzal a pozitív tényezővel való szorzás útján keletkezik, tehát

P

és

R

egy az

R_{0}

-ból induló félegyenesen van. Ezzel leírtuk geometriailag azt a transzformációt, amely az

(1^{*})

(2^{*})

képleteknek megfelelően rendeli minden az

R_{0}

-tól különböző

R (ξ, η)

ponthoz a

P

(x, y)

pontot. Ennél a transzformációnál speciálisan azok az

R

pontok önmaguknak felelnek meg, amelyekre

R_{0} R = \sqrt[]{2}

, vagyis az

R_{0}

középpontú,

r = \sqrt[]{2}

sugarú

k

kör pontjai és más pont nem.
Ha a feladat feltételei teljesülnek, és

u \neq 0

, akkor

η / ξ = - v / u = - m \neq 0

is állandó, tehát az ilyen pontok egy-egy, az origón átmenő és az

x

y

tengelyektől különböző egyenesen vannak. Így a feladatot geometriailag a következővé alakítottuk át: A leírt transzformáció mibe visz át egy a

k

kört két pontban metsző, annak

R_{0}

középpontján nem átmenő, tetszőleges

e

egyenest?
Legyenek

e

és

k

metszéspontjai

A

és

B

R

legyen az

e

tetszőleges, az

A

B

pontoktól különböző pontja, és

P

R_{0} R

félegyenes azon pontja, amelyre (11) teljesül (2. ábra).

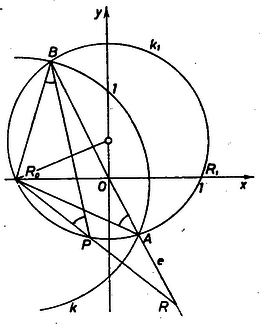2. ábra

Feltehetjük, hogy

R

B A

félegyenesen van. Az

R_{0} B R

és

R_{0} P B

háromszögek

R_{0}

-nál levő szöge közös és e szög szárain levő oldalakra (11) alapján

\begin{matrix} R_{0} B : R_{0} R = R_{0} P : R_{0} B, \end{matrix}

e két háromszög tehát hasonló, így

\begin{matrix} R_{0} B R ∢ = R_{0} P B ∢ . \end{matrix}

A B R_{0}

háromszög egyenlő szárú, tehát

R_{0} B R ∢ = R_{0} A B ∢

, így az

R_{0} B

szakasz az

A

és

P

pontokból egyenlő szög alatt látszik,

P

tehát rajta van az

A B R_{0}

háromszög köré írható

k_{1}

körön. Megfordítva: a

k_{1}

kör tetszőleges,

R_{0}

-tól különböző

P

pontjához van olyan

R

pontja

e

-nek, melyet transzformációnk éppen

P

-be visz. Valóban, messe az

R_{0} P

egyenes

e

-t

R

-ben.

R

-hez az előbbiek szerint a transzformáció a

k_{1}

kör és az

R_{0} R

egyenes

R_{0}

-tól különböző metszéspontját, vagyis

P

-t rendeli hozzá.
Visszatérve a koordináta-rendszerbe, az origón átmenő,

- m

meredekségű egyenesek képe a fentiek alapján egy

k_{1}

kör lesz, mely átmegy az

R_{0}

ponton és az origó képén, az

R_{1} (+ 1,

0)

ponton. Mivel az

R_{0} R_{1}

szakasz felező merőlegese, az

y

tengely,

k_{1}

-nek átmérője, azért

k_{1}

középpontja is az

y

tengelyen van. Mint láttuk,

k_{1}

-nek az eredeti

e

egyenesre merőleges,

R_{0}

-on átmenő egyenes is átmérője, a középpont tehát az

R_{0}

-on átmenő,

(+ \frac{1}{m})

meredekségű egyenesnek az

y

tengellyel alkotott metszéspontja, azaz a

(0, \frac{1}{m})

koordinátájú pont; így

k_{1}

sugara

\begin{matrix} r = \sqrt[]{1 + \frac{1}{m^{2}}}, \end{matrix}

és egyenlete:

\begin{matrix} x^{2} + {(y - \frac{1}{m})}^{2} = 1 + \frac{1}{m^{2}} . \end{matrix}

Eleve nem tartozik

k

-hoz a kivételes

R_{0}

pont, és mivel a

v / u = m \neq 0

feltétellel az origót is kizártuk, ennek képe, az

R_{1}

pont sem tartozik az (1), (2) egyenletekkel leírt görbéhez. A fentiekből viszont következik, hogy

k_{1}

minden más pontja az (1)‐(2) görbéhez tartozik.
(Tusnády Gábor)