| Feladat: | 1594. matematika feladat | Korcsoport: 18- | Nehézségi fok: átlagos |
| Megoldó(k): | Backhausz Beáta , Csetényi A. , Fischer Ágnes , Gegesy F. , Kemény András , Komjáth P. , Koren A. , Kovalszky R. , László I. , Lempert L. , Máthé Mariann , Siklósi M. , Somogyi Á. , Sztrapkovics László | ||
| Füzet: | 1968/december, 204 - 205. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Exponenciális egyenletek, Paraméteres egyenletek, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1968/március: 1594. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Mivel minden pozitív alapú exponenciális függvény értékkészlete pozitív, így egyenletünk ekvivalens a -nel való átosztás útján keletkező
Mivel is csak pozitív lehet, azt kell eldöntenünk, ennek hány pozitív megoldása lehet. esetén (2) elsőfokú egyenlet, csak lehet, és ez -re egy megoldást ad, ha , mert az exponenciális függvény minden pozitív értéket egyetlen helyen vesz föl. Hasonlóan esetén csak az gyök ad egy megfelelő értéket, amennyiben . Ha , egyike sem , akkor (2)-ből A zárójelből adódó két érték egymással ellenkező előjelű, ha , s így -ra is, tehát -re is egy pozitív értéket kapunk, bármi is az . Ha , akkor a zárójelbeli értékek pozitívok, így pozitív esetén két pozitív (és ) érték adódik, negatív esetén egy sem. -re pozitív, ha pozitív, negatív -re ismét nincs (1)-nek megoldása, és ugyancsak nincs megoldás, ha . 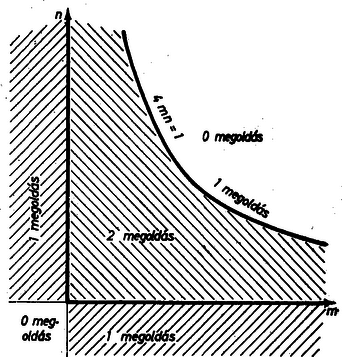 A megoldások számát az , koordináta-rendszerben az ábra tünteti fel vonalanként, ill. síkrészenként. Kemény András (Budapest, Berzsenyi D. Gimn., II. o. t.) Sztapkovics László (Budapest, Fazekas M. Gyak. Gimn., II. o. t.) |