Kezdőlap


Feladat:	1592. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Nagy András
Füzet:	1968/november, 134 - 136. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Térfogat, Térelemek és részeik, Feladat
Hivatkozás(ok):	Feladatok: 1968/február: 1592. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Tekintsük az említett $A B C D E$ ötszöglapot a $P$ poliéder alaplapjának úgy, hogy $A B = a$ , $A E = b$ , $D E = a / 2$ , ekkor $B C = b / 2$ . A további lapok száma $5$ , így mindegyiküknek van éle az alapon, és az alapsíkra merőleges lap a $C D$ élhez kapcsolódik; legyen ennek harmadik csúcsa $F$ , a hátra levő $7$ . csúcs pedig 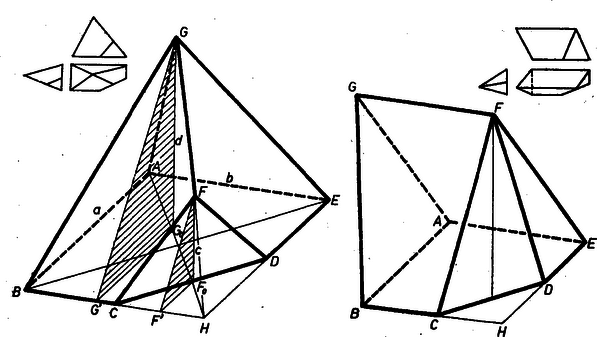$G$ .
A $C B$ és $D E$ alapélre támaszkodó oldallapoknak a konvexség miatt át kell menniük $F$ -en. $P$ további vizsgálata aszerint alakul, hogy $F$ -ben csak a mondott $3$ lap metszi egymást, vagy még további lap is.
Ha $F$ $3$ -lapú csúcs ‐ azaz egyszersmind $3$ -élű is ‐, akkor $P$ -nek $F$ -ből kiinduló harmadik élét az $F C B$ , $F D E$ oldallapsíkok metszésvonala tartalmazza (1. ábra). A metszésvonal az alaplap síkját a $B C$ , $E D$ egyenesek metszéspontjában, a téglalap lemetszett $H$ csúcsában döfi át, másrészt átmegy $G$ -n, hiszen az $5$ alapcsúcs egyikén sem mehet át. E metszésvonalnak egyetlen pontja van az alap fölött $d$ magasságban, eszerint $G$ egyértelműen meg van határozva, hacsak $d > c$ , hiszen a konvexség miatt $G$ -nek a $C D F$ sík $A$ -t tartalmazó oldalán kell lennie, vagyis a $H F$ szakasz $F$ -en túli meghosszabbításán. ‐ Ezek szerint az $F$ -ben összefutó lapok a $B C F G$ , $E D F G$ négyszögek, a hátra levő $2$ lap pedig a konvexség alapján az $A B G$ és $A E G$ háromszög. Ebben az esetben $P$ -t az $A B H E G$ gúlából is származtathatjuk a $H C D F$ gúla lemetszése útján.

1. ábra 2. ábra

Amennyiben

F

a poliéder további oldallapjának is csúcsa ‐ ti. az alaphoz a

B C

C D

D E

élen kapcsolódó lapokon túl ‐, ez csak az egyik lehet az alaphoz a hátra levő

E A

és

A B

élen kapcsolódó lapok közül, különben ugyanis a keletkező konvex poliéder ötoldalú gúla lenne, és nem lehetne

7

. csúcsa. Elég azt az esetet tekintenünk, ha az

F

-en átmenő negyedik oldallapsík az

E A

élen kapcsolódik, hiszen a másik lehetőség ebbe megy át a

B

E

és

C

D

betű-párok egyidejű fölcserélésével, és ez a fölcserélés az alapidom tulajdonságait változatlanul hagyja (2. ábra).
Ekkor az

F

-ben összefutó

4

lapsík egymásutánja (

3

‐

3

ponttal meghatározva)

F B C

F C D

F D E

F E A

, és így az utolsó lap az első laphoz élben csatlakozik. S mivel e két sík tartalmazza a téglalap szemben fekvő, tehát párhuzamos

B H

A E

oldalegyenesét, azért az

F

-en áthaladó metszésvonaluk is párhuzamos ezekkel, és így az alap síkjával is. Ezen kell lennie

G

-nek, ilyen megoldás tehát csak

d = c

esetén lehetséges, és megfordítva: e feltétel mellett nincs is más megoldás.
Így azonban

G

-ként szerepelhet az

F

-ből kiinduló és

E A

-val egyirányú félegyenes bármely pontja, tehát

P

nincs egyértelműen meghatározva.
II.

P

felszínének és térfogatának kérdését csak az előbbi (azaz

d > c

feltételű) esetben vizsgálhatjuk (1. ábra).

P

térfogata, mint az

A B H E G

és

C H D F

gúlák térfogatának különbsége

\begin{matrix} V = \frac{a b d}{3} - \frac{1}{2} \cdot \frac{a}{2} \cdot \frac{b}{2} \cdot \frac{c}{3} = \frac{a b}{24} (8 d - c) . \end{matrix}

a numerikus adatokkal

4625

térfogategység.
III. A

G F C B

G F D E

lapok területét szintén a lemetszésre támaszkodva számítjuk. Legyen

G

és

F

vetülete a

B C

egyenesen

G'

F'

, az alaplap síkján

G_{0}

F_{0}

, a legutóbbi felezi a

C D

alapélt, ennélfogva negyedeli a téglalap

H A

átlóját, így pedig a fentiek szerint

G_{0}

is rajta van az átlón. Ezért

G G' G_{0}

és

F F' F_{0}

, valamint

H G' G_{0}

és

H F' F_{0}

hasonló háromszögek, így

G_{0}

-nak a

B C

E D

egyenestől való távolsága

\begin{matrix} G_{0} G' = \frac{d}{c} \cdot F_{0} F' = \frac{a d}{4 c}, G' H = \frac{d}{c} \cdot F' H = \frac{b d}{4 c}, \end{matrix}

ennélfogva az

A E

A B

egyenestől való távolsága

\begin{matrix} | \frac{a d}{4 c} - a | = \frac{a}{4 c} \cdot | d - 4 c |, \\ | \frac{b d}{4 c} - b | = \frac{b}{4 c} \cdot | d - 4 c | . \end{matrix}

Így a

G B H

G H E

G E A

G A B

oldalháromszög magassága:

\begin{matrix} (G G' =) \frac{d}{4 c} \cdot \sqrt[]{a^{2} + 16 c^{2}}, \frac{d}{4 c} \cdot \sqrt[]{b^{2} + 16 c^{2}}, \\ \sqrt[]{\frac{a^{2}}{16 c^{2}} {(d - 4 c)}^{2} + d^{2}}, \sqrt[]{\frac{b^{2}}{16 c^{2}} {(d - 4 c)}^{2} + d^{2}}, \end{matrix}

és hasonlóan az

F C H

F H D

háromszög

F

-ből induló magassága

\begin{matrix} \frac{1}{4} \sqrt[]{a^{2} + 16 c^{2}}, \frac{1}{4} \sqrt[]{b^{2} + 16 c^{2}} . \end{matrix}

P

felszínét most már úgy kapjuk, hogy e

6

magasságot rendre megszorozzuk a megfelelő alap felével:

b / 2

-vel,

a / 2

-vel,

b / 2

-vel,

a / 2

-vel,

(- b / 4)

-gyel,

(- a / 4)

-gyel, és e szorzatok összegéhez hozzáadjuk a

C D F

háromszög és az alaplap területének összegét. Alkalmas összevonásokkal:

\begin{matrix} F_{P} = \frac{b}{16 c} (2 d - c) \sqrt[]{a^{2} + 16 c^{2}} + \frac{a}{16 c} (2 d - c) \sqrt[]{b^{2} + 16 c^{2}} + \\ + \frac{b}{8 c} \sqrt[]{a^{2} {(d - 4 c)}^{2} + 16 c^{2} d^{2}} + \frac{a}{8 c} \sqrt[]{b^{2} {(d - 4 c)}^{2} + 16 c^{2} d^{2}} + \frac{c}{4} \sqrt[]{a^{2} + b^{2}} + \frac{7}{8} a b . \end{matrix}

A számadatokkal

F_{P} = 1851, 6

területegység.

Nagy András (Budapest, Toldy F. Gimn., III. o. t.) dolgozata alapján.

Megjegyzés.

d = 4 c

esetén

G_{0}

A

csúcsba esik, és

F_{P}

képlete némileg egyszerűbbé válik.