Kezdőlap


Feladat:	1591. matematika feladat	Korcsoport: 14-15	Nehézségi fok: -
Megoldó(k):	Backhausz Beáta , Bálványos Z. , Csirmaz L. , Hárs L. , Jánossy D. , Katona V. , Kemény A. , Kóczy L. , Kovalszky R. , Lempert L. , Lengyel Tamás , Nagy András , Nagy Dénes , Nagy Zsigmond , Radó P. , Tél T. , Turi A. , Váli L. , Zambó Péter
Füzet:	1970/november, 100 - 102. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Háromszögek hasonlósága, Pont körüli forgatás, Körülírt kör, Súlypont, Műveletek helyvektorok koordinátáival, Sokszögek súlypontjának koordinátái, Síkgeometriai számítások trigonometria nélkül háromszögekben, Feladat
Hivatkozás(ok):	Feladatok: 1968/február: 1591. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az $S$ -en át berajzolt három szakasz végpontjai harmadolják az oldalakat. Jelöljük a $6$ harmadoló pontot egyformán $D$ -vel és indexbe írva az illető oldal végpontjainak betűjelét, éspedig elöl a harmadoló ponthoz közelebbi végpont jelét, tehát pl. $B D_{B C} = D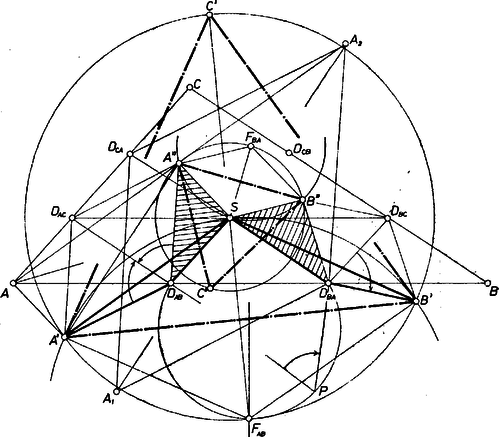_{B C} D_{C B} = D_{C B} C = a / 3$ (1. ábra).

1. ábra

Továbbá mindegyik berajzolt szakasz hossza

2 / 3

része a vele párhuzamos oldalnak, és

S

felezi a szakaszt; az egy csúcsból induló két oldal harmadoló pontjait összekötő szakaszok ugyancsak párhuzamosak a szemben levő oldallal és hosszuk annak

1 / 3

része: pl.

S D_{B A} = S D_{C A} = D_{A B} D_{A C} = a / 3

.
Eszerint

A_{1}

és

A_{2}

D_{B A} D_{C A}

szakasz fölötti szabályos háromszögek csúcsai, az

A' A''

szakasz az

A_{1} A_{2}

-nek,

D_{A B} D_{A C}

pedig a

D_{B A} D_{C A}

-nak felére kicsinyített képe

A

-ból mint centrumból, így

A' D_{A B} D_{A C}

és

A'' D_{A B} D_{A C}

is szabályos háromszögek, oldaluk hossza

a / 3

, és ugyanígy

B' D_{B C} D_{B A}

és

B'' D_{B C} D_{B A}

b / 3

oldalú szabályos háromszögek.
Megmutatjuk, hogy az

A' D_{A B} S

és

S D_{B A} B'

háromszögek egybevágók és egymásba egy alkalmas elfordítással átvihetők. Bizonyításunkat az ábra pozitív körüljárású

A B C

háromszögéből létrejött alakzatra végezzük. Valóban,

\begin{matrix} | \vec{D_{A B} A'} | = | \vec{D_{A B} D_{A C}} | = | \vec{D_{B A} S} | = a / 3, | \vec{D_{A B} S} | = | \vec{D_{B A} D_{B C}} | = | \vec{D_{B A} B'} | = b / 3 \end{matrix}

és

\begin{matrix} A' D_{A B} S ∢ = S D_{B A} B' ∢, \end{matrix}

mert a

D_{A B} A'

irányt a

D_{A B} D_{A C}

-vel egyirányú

D_{B A} S

irányba ugyanúgy

(- 60^{\circ})

-os elfordítás viszi át, mint a

D_{A B} S

és

D_{B A} D_{B C}

irányokat a

D_{B A} B'

-be. Ezért

A' S = S B'

, a mondott elfordítás

F_{A B}

középpontja pedig a

D_{A B} D_{B A}

szakasz fölé a

C

-t nem tartalmazó partján szerkesztett szabályos háromszög új csúcsa, mert az elfordítás középpontja rajta van egyrészt a

D_{A B} D_{B A}

szakasz felező merőlegesén, másrészt azon a látószögköríven, melynek

P

pontjaira a

D_{A B} P D_{B A}

forgásszög nagysága

(- 60^{\circ})

. Így

A' F_{A B} S

és

S F_{A B} B'

szabályos háromszögek, tehát

A' S B' ∢ = 120^{\circ}

.
Bizonyításunkban minden egyes

A

B

C

betű (indexbeli is) helyére rendre

B

C

A

betűt és

D

S

F

helyére önmagát írva

B' S = S C'

adódik, ezt a fentivel egybevetve

A'

B'

C'

valóban egyenlő távolságra vannak

S

-től, továbbá

B' S C' ∢ = 120^{\circ}

, tehát

H'

szabályos háromszög.
Ugyanígy az

A'' D_{A B} S

és

S D_{B A} B''

egymásba fordíthatók, mert az

A'' D_{A B}

és

S D_{B A}

oldalak

(+ 60^{\circ})

-os elfordítással, ill. párhuzamos eltolással a

D_{A B} D_{A C}

szakaszon egymással fedésbe jutnak, ugyanúgy

D_{A B} S

és

D_{B A} B''

D_{B A} D_{B C}

szakaszon ‐ eltolással, ill.

(+ 60^{\circ})

-os forgással ‐, így a 2‐2 oldalszakaszból álló

A'' D_{A B} S

törött vonal valamilyen középpont körüli

60^{\circ}

-os elfordulással átjut az

S D_{B A} B''

törött vonalba, tehát

S A''

záró oldala

B'' S

-be jut, így pedig e szakaszok egyenlők. Az elfordulás középpontja a fentihez hasonló megokolással a

D_{A B}

-t

D_{B A}

-ba vivő

(+ 60^{\circ})

-os forgás középpontja, vagyis a

D_{A B} D_{B A}

szakasz fölé a

C

-t tartalmazó oldalán szerkesztett szabályos háromszög új,

F_{B A}

csúcsa. Ebből a fentiekhez hasonlóan

A'' S B'' ∢ = 120^{\circ}

, továbbá a fentihez hasonló megismétléssel

S

A'' B'' C''

szabályos háromszög középpontja.

Lengyel Tamás (Budapest, Berzsenyi D. Gimn.)

II. megoldás a feladat állító részére. Helyezzük koordináta-rendszerünk origóját

S

-be,

x

tengelyének iránya legyen a

B C

irány, a

B C

oldal hossza

a

, felezőpontjának abszcisszája

p

, ordinátájának abszolút értéke így az

m_{a}

magasság

1 / 3

része, legyen az előjele negatív: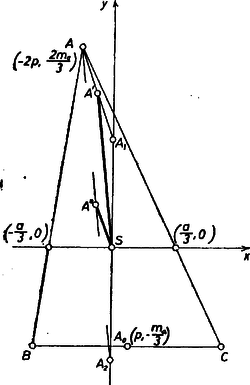

A_{0} (p, - m_{a} / 3)

2. ábra

Ekkor a súlypont harmadoló tulajdonsága folytán

A (- 2 p,2 m_{a} / 3)

, a szerkesztett szabályos háromszögek közös alapjának végpontjai az

x

tengelyen

(- a / 3,0)

(a / 3,0)

és a további pontok (2. ábra):

\begin{matrix} A_{1} (0, a / \sqrt[]{3}), A_{2} (0, - a / \sqrt[]{3}); A' (- p, m a / 3 + a / 2 \sqrt[]{3}), A'' (- p, m_{a} / 3 - a / 2 \sqrt[]{3}), \end{matrix}

végül az utóbbi kettőnek

S

-től való távolsága:

\begin{matrix} S A'^{2} = p^{2} + \frac{m_{a}^{2}}{9} + \frac{a^{2}}{12} + \frac{a m_{a}}{3 \sqrt[]{3}}, S A''^{2} = p^{2} + \frac{m_{a}^{2}}{9} + \frac{a^{2}}{12} - \frac{a m_{a}}{3 \sqrt[]{3}} . \end{matrix}

Megmutatjuk, hogy e két kifejezés a háromszög oldalainak szimmetrikus függvénye, egyforma módon függ az

a

b

c

oldalhosszak mindegyikétől. Ebből már következik, hogy a számítást

B'

-re és

C'

-re, ill.

B''

-re és

C''

-re ismételve az eredmény ugyanaz, a feladat állítása helyes. (A számítás természetesen nem lenne ilyen egyszerű, a tengelyek más állása folytán.)
A kifejezések utolsó, megkülönböztető tagjában a számláló a terület

2

-szerese, állításunk erre a tagra nyilvánvaló.
Az első két tag összege az

A_{0}

és az origó közti távolság négyzetét adja, vagyis az

A A_{0} = s_{a}

súlyvonal négyzetének

1 / 9

részét. Ámde ismert képlet szerint^{$^{*}$}

\begin{matrix} s_{a}^{2} = \frac{2 b^{2} + 2 c^{2} - a^{2}}{4}, \end{matrix}

ezzel kifejezéseink közös első három tagja állításunk szerint alakul:

\begin{matrix} \frac{s_{a}^{2}}{9} + \frac{a^{2}}{12} = \frac{a^{2} + b^{2} + c^{2}}{18} . \end{matrix}

Ezzel a feladat állítását bebizonyítottuk, sőt valamivel többet végeztünk, megadtuk a

H'

H''

háromszög köré írható kör sugarát az eredeti háromszög oldalainak függvényében.
Nyilvánvalóan minden háromszögben

S A'^{2} > 0

, másrészt

S A''^{2} \geq 0

, meg lehet ugyanis mutatni,^{$^{*}$} hogy a közös nevezőre hozott alak számlálója

\begin{matrix} a^{2} + b^{2} + c^{2} - 4 \sqrt[]{3} t \geq 0, \end{matrix}

és egyenlőség csak szabályos háromszög esetében teljesül (amikor

A''

nyilvánvalóan

S

-ben adódik).

^{$^{*}$}Pl. az

A B A^{*} C

paralelogrammában:

\begin{matrix} A A^{* 2} + B C^{2} = A B^{2} + B A^{* 2} + A^{*} C^{2} + C A^{2}, 4 s_{a}^{2} = 2 b^{2} + 2 c^{2} - a^{2} . \end{matrix}

^{$^{*}$}A III. Nemzetközi Matematikai Diákolimpia feladata, Veszprém, 1961, lásd K. M. L. 1128. feladat, 24. kötet, 208. o. (1962. május hó). ‐ Rokonságban van a feladattal az 1527. feladat is, K. M. L. 36 (1968) 99. o.