Kezdőlap


Feladat:	1581. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Cseh J. , Draschitz R. , Ésik Z. , Gegesy F. , Kovács József , Kovalszky Róbert , Munk S. , Nagy Zsigmond , Sax Gy. , Takács Andor , Viszkei Gy. , Zambó Péter
Füzet:	1969/május, 195 - 198. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül háromszögekben, Síkgeometriai szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 1968/január: 1581. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. 1. Először olyan területfelező egyenest keresünk $D$ -n át, amely az $A B, A C$ szakaszt metszi egy $E$ , ill. $F$ pontban. Jelöljük az adott $0, 32$ és $0, 36$ arányszámot $p_{c}$ -vel, ill. $p_{b}$ -vel, ekkor a $D A E$ és $D A F$ háromszögnek $D$ -ből húzott magassága $p_{c} m_{c}$ , ill. $p_{b} m_{b}$ , ahol $m_{c}, m_{b}$ az eredeti háromszög $C$ -ből, ill. $B$ -ből húzott magassága. Legyen továbbá $A E / A B = q_{c}$ és $A F / A C = q_{b}$ , vagyis $A E = q_{c} A B = q_{c} c$ , $A F = q_{b} A C = q_{b} b$ , és az $A E F$ háromszög $F$ -ből induló magassága $q_{b} m_{c}$ .
Minthogy $A E D + A D F = A E F$ (a háromszögek területét ugyanúgy jelöltük, mint magukat a háromszögeket), azért

\begin{matrix} \frac{q_{c} c \cdot p_{c} m_{c}}{2} + \frac{q_{b} b \cdot p_{b} m_{b}}{2} = \frac{q_{c} c \cdot q_{b} m_{c}}{2}, \end{matrix}

amit

A B C = c m_{c} / 2 = b m_{b} / 2

-vel osztva

\begin{matrix} q_{c} p_{c} + q_{b} p_{b} = q_{c} q_{b}, \end{matrix}

és innen

\begin{matrix} q_{b} = \frac{q_{c} p_{c}}{q_{c} - p_{b}} . \end{matrix}

(1)

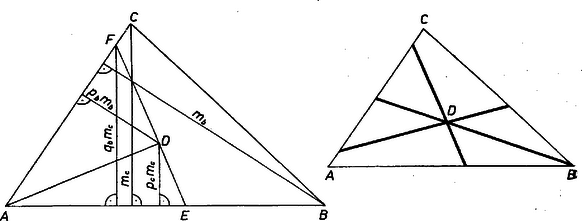1. ábra 2. ábra

Ezt az

A E F = A B C / 2

, egyszerű alakítással

q_{b} q_{c} = 1 / 2

követelménybe helyettesítve

\begin{matrix} \frac{p_{c} q_{c}^{2}}{q_{c} - p_{b}} = \frac{1}{2}, 2 p_{c} q_{c}^{2} - q_{c} + p_{b} = 0, \\ q_{c} = \frac{1 \pm \sqrt[]{1 - 8 p_{b} p_{c}}}{4 p_{c}} . & (2) \end{matrix}

Ez csak akkor felel meg követelményünknek, ha teljesül

0 < q_{c} \leq 1

, továbbá (1)-ből

0 < q_{b} \leq 1

.
Esetünkben

p_{c} = 0, 32

és

p_{b} = 0, 36

felhasználásával mindkét értékpár megfelel, ugyanis

\begin{matrix} q_{c}' & = \frac{9}{16}, q_{c}'' = 1; \\ q_{b}' & = \frac{8}{9}, q_{b}'' = \frac{1}{2} . & (3) \end{matrix}

Ezzel két területfelező egyenest kaptunk

D

-n át, könnyű látni, hogy az utóbbi

A B

-t a

B

végpontban metszi és ez a felező az eredeti háromszög

B

-ből induló

B B_{0}

súlyvonala.
2. Eredményeink a betűzés kellő megváltoztatásával felhasználhatók azoknak a területfelezőknek a meghatározására, amelyek a

B

-ből és a

C

-ből kiinduló oldalszakasz-párt metszik át, ehhez csupán azt kell tudnunk, az

A

-ból induló magasságnak hányadrészét teszi ki

D

-nek

B C

-től való távolsága; legyen ez az arányszám

p_{a}

. Ezzel kifejezve a

D A B + D B C + D C A = A B C

összefüggés így alakul:

\begin{matrix} \frac{c p_{c} m_{c}}{2} + \frac{a p_{a} m_{a}}{2} + \frac{b p_{b} m_{b}}{2} = \frac{c m_{c}}{2} = \frac{a m_{a}}{2} = \frac{b m_{b}}{2}, \\ p_{a} + p_{b} + p_{c} = 1, tehát p_{a} = 0, 32. \end{matrix}

Mármost észrevéve, hogy

p_{a} = p_{c}

, a

C B

és

C A

oldalszakaszokat metsző területfelezőre az

A

és

C

, valamint

a

és

c

betűk cseréje után ismét a (3) értékeket kapjuk, a második értékpár azonban újra a

B B_{0}

súlyvonalat adja meg.
Végül a

B A, B C

oldalszakaszpárt metsző területfelező egyenest nem kapunk, mert az

A, B, C

betűk helyére mindenütt rendre

B

-t,

C

-t,

A

-t írva (2)-ből és (1)-ből

\begin{matrix} q_{a} = \frac{1 \pm \sqrt[]{1 - 8 p_{c} p_{a}}}{4 p_{a}}, q_{a} = \frac{q_{a} p_{a}}{q_{a} - p_{c}}, \end{matrix}

és az egyik megoldásban

q_{a}' > 1

, a másikban

q_{c}'' > 1

(egyébként

q_{c}'' = q_{a}'

). A talált 3 területfelezőt a 2. ábra mutatja.
Kovalszky Róbert (Budapest, Landler J. Gimn.)

Megjegyzések. 1. Vegyük észre, hogy az

A B C

háromszög alak szerint nem volt meghatározva, eredményünk bármely háromszögnek a

p_{b}, p_{c}

arányokkal meghatározott

D

pontjára érvényes.
2. Az adott arányértékek mellett

D

mindig rajta van a háromszög

B

-ből induló

B B_{0}

súlyvonalán, a másik két területfelező pedig egymás képe abban a ferde tükrözésben, melyben a megfelelő pontokat összekötő szakasz párhuzamos

A C

-vel és a köztük levő szakaszt

B B_{0}

felezi.

II. megoldás (vázlat). A kitűzésben ajánlott 1455. feladat egy adott

D

ponthoz egyetlen területfelező egyenes szerkesztését írta le és bizonyította be, viszont (a III. rész végén) utalt arra, hogy a háromszögön belüli

D_{1}

esetében ‐ amilyen az itteni

D

pont is ‐ egy további területfelező is lehetséges, a szerkesztés utolsó lépésében felmérendő szakaszt az ellentétes irányban felmérve. Ez ‐ mint látni fogjuk ‐ esetünkben is ad második megoldást.
A mondott szerkesztés lépéseit az 1455. feladat bizonyítása szerinti számítással követjük (3. ábra).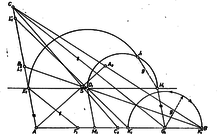

3. ábra

D_{1}

-en átmenő,

A B

-vel párhuzamos egyenesnek

A C

-vel való

E_{1}

metszéspontjára nézve az

A E_{1} D_{1} M_{1}

paralelogrammából a feltevés szerint

E_{1} D_{1} = A M_{1} = 0, 36 A B = 9 A B / 25

, másrészt

A E_{1} = 0, 32 A C = 8 A C / 25

.
Arra a

G_{1}

pontra nézve, melyet az

A B

-t negyedelő

F_{1}

pont és

E_{1}

összekötő egyenesével

C

-n át húzott párhuzamos metsz ki

A B

-ből, hasonlóság alapján

\begin{matrix} A G_{1} = A F_{1} \cdot \frac{A C}{A E_{1}} = \frac{A B \cdot A C}{4 A E_{1}} = \frac{25}{32} A B, \end{matrix}

továbbá mivel

H_{1}

paralelogrammává egészíti ki

E_{1} A G_{1}

-et,

\begin{matrix} D_{1} H_{1} = E_{1} H_{1} - E_{1} D_{1} = A G_{1} - E_{1} D_{1} = A B (\frac{25}{32} - \frac{9}{25}) . \end{matrix}

Így a körzővel átviendő szakasz hossza, a

D_{1} H_{1}

átfogóval és

D_{1} E_{1}

befogóval szerkesztett derékszögű háromszög másik befogója:

\begin{matrix} g = \sqrt[]{D_{1} H_{1}^{2} - D_{1} E_{1}^{2}} = A B \sqrt[]{{(\frac{25}{32} - \frac{9}{25})}^{2} - {(\frac{9}{25})}^{2}} = A B \sqrt[]{\frac{25}{32} (\frac{25}{32} - \frac{18}{25})} = \frac{7}{32} A B . \end{matrix}

Ezt

G_{1}

-től

A

felé felmérve kapjuk a

D_{1}

-en átmenő, az eljárás szerinti területfelező egyenesnek

A B

-n levő

K_{1}'

pontját:

\begin{matrix} A K_{1}' = A G_{1} - g = \frac{9}{16} A B, \end{matrix}

viszont az ellentétes irányú felméréssel is az

A B

szakasz egy pontját, ti. a végpontját kapjuk:

A K_{1}'' = A G_{1} + g = A B

, tehát

K_{1}''

azonos

B

-vel. Végül a felezőknek az

A C

szakaszon levő

L_{1}

pontjára, hasonló háromszögekből

\begin{matrix} A L_{1}' = A E_{1} \cdot \frac{A K_{1}'}{M K_{1}'} = \frac{8}{9} A C, A L_{1}'' = A E_{1} \cdot \frac{A K_{1}''}{M K_{1}''} = \frac{1}{2} A C . \end{matrix}

A kapott második területfelező egyenes azonos a

B B_{0}

súlyvonallal. Így

D_{1}

az 1455. feladatban vizsgált

C_{0} S B

szögtartomány határán van, vagyis a

B S A_{0}

szögtartományhoz is hozzátartozik, ezért az eljárást az

A

és

C

betűk felcserélésével végrehajtva újabb területfelezőt kapunk.
(Bizonyítani kellene még, hogy az így talált 3-nál több területfelező nem lehetséges; ezt itt mellőzzük.)