Kezdőlap


Feladat:	1580. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Pál Jenő
Füzet:	1968/november, 125 - 128. oldal		PDF \| MathML
Témakör(ök):	Függvényvizsgálat, Feladat
Hivatkozás(ok):	Feladatok: 1968/január: 1580. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A kifejezést az $x$ változó egyetlen trigonometrikus függvényének függvényévé alakítjuk. Ismert azonosságok alapján

\begin{matrix} y = \frac{1}{2} (1 - cos 2 x + \frac{\sqrt[]{7}}{3} sin 2 x) . \end{matrix}

(1)

Szorozzuk és osszuk a változó részt az egyelőre ismeretlen

c

állandó számmal és határozzuk ezt úgy meg, hogy

cos 2 x

és

sin 2 x

szorzója egy

φ

pozitív vagy negatív hegyesszög színusza, ill. koszinusza legyen:

\begin{matrix} y = \frac{1}{2} + \frac{1}{2 c} (\frac{\sqrt[]{7} c}{3} sin 2 x - c cos 2 x), \\ \frac{\sqrt[]{7} c}{3} = cos φ, - c = sin φ, \end{matrix}

amiből

\begin{matrix} tg φ = - \frac{3}{\sqrt[]{7}}, φ = - 48^{\circ} 36', \end{matrix}

és így, a

sin x

függvény addíció tétele alapján

\begin{matrix} c = - sin φ = - \frac{tg φ}{\sqrt[]{1 + {tg}^{2} φ}} = \frac{3}{4}, \\ y = \frac{1}{2} + \frac{2}{3} sin (2 x + φ) . \end{matrix}

Ennek legnagyobb értéke

\begin{matrix} y_{max} = \frac{1}{2} + \frac{2}{3} = \frac{7}{6}, \end{matrix}

amikor

\begin{matrix} 2 x + φ = (4 k + 1) \cdot 90^{\circ}, \end{matrix}

és

k

olyan egész szám, hogy

\begin{matrix} 0^{\circ} \leq x = (4 k + 1) \cdot 45^{\circ} - \frac{φ}{2} \leq 360^{\circ}, \end{matrix}

vagyis

k = 0

és

k = 1

esetén, amikor

\begin{matrix} x_{max} = 69^{\circ} 18' és 249^{\circ} 18' . \end{matrix}

Legkisebb értéke pedig

\begin{matrix} y_{min} = \frac{1}{2} - \frac{2}{3} = - \frac{1}{6}, \end{matrix}

ahol az előbbihez hasonlóan,

\begin{matrix} 2 x + φ = (4 k + 3) \cdot 90^{\circ}, \end{matrix}

és

k = 0

1

esetén

x

megfelelő értékei

\begin{matrix} x_{min} = 159^{\circ} 18' és 339^{\circ} 18' . \end{matrix}

Pál Jenő (Kaposvár, Táncsics M. Gimn., II. o. t.)

Megjegyzések. 1. A fenti

c

szorzó abszolút értékét meghatározhatjuk a

sin^{2} φ + cos^{2} φ = c^{2} (1 + \frac{7}{9}) = \frac{16}{9} c^{2} = 1

összefüggésből is, előjele pedig egyezik

cos φ

előjelével, ezért

- 90^{\circ} < φ < 90^{\circ}

alapján

c > 0

.
2. Lényegében azonos a fentivel a következő alakítás, sokan jártak ezen az úton is:

\begin{matrix} y = sin x (sin x + \frac{\sqrt[]{7}}{3} cos x) = \frac{4}{3} sin x sin (x + φ) = \frac{2}{3} [cos φ - cos (2 x + φ)], \end{matrix}

ahol

tg φ = \sqrt[]{7} / 3

, és így

cos φ = 3 / 4

II. megoldás. Az ismert

\begin{matrix} sin x = \frac{2 tg x / 2}{1 + {tg}^{2} x / 2}, cos x = \frac{1 - {tg}^{2} x / 2}{1 + {tg}^{2} x / 2} \end{matrix}

azonosságokat

x

helyén

2 x

-szel (1)-re alkalmazva

\begin{matrix} y = \frac{{tg}^{2} x + (\sqrt[]{7} / 3) tg x}{1 + {tg}^{2} x}; \end{matrix}

(2)

ezzel

y

-t ismét egyetlen szög egyetlen trigonometrikus függvényének függvényeként állítottuk elő. A feladat első része lényegében (2) értékkészletét, ennek határait kérdezi, vagyis azoknak az

y

-oknak a halmazát, amelyekre (2)-nek van megoldása

x

-re. Az átrendezéssel adódó

\begin{matrix} (y - 1) {tg}^{2} x - \frac{\sqrt[]{7}}{3} tg x + y = 0 \end{matrix}

(3)

egyenlet

tg x

-re másodfokú, hacsak

y - 1 \neq 0

, és ekkor diszkriminánsa

\begin{matrix} D = \frac{7}{9} - 4 y (y - 1) = - 4 (y + \frac{1}{6}) (y - \frac{7}{6}) . \end{matrix}

Ez akkor nem negatív, ha a változó tényezők kisebbike nem pozitív és nagyobbika nem negatív, azaz

\begin{matrix} y - \frac{7}{6} \leq 0 és y + \frac{1}{6} \geq 0, összefoglalva \\ - \frac{1}{6} \leq y \leq \frac{7}{6} . & (4) \end{matrix}

A kivételes

y = 1

eset beleesik ebbe az intervallumba.
(3)-ból a

D = 0

esetekben egyetlen megoldásként

\begin{matrix} tg x = \frac{\sqrt[]{7}}{6 (y - 1)}, vagyis \\ y = - \frac{1}{6} esetén tg x = - \frac{\sqrt[]{7}}{7} = - 0, 3780, \\ y = \frac{7}{6} esetén tg x = \sqrt[]{7} = 2, 646, \end{matrix}

vagyis a (4)-beli határokat függvényének föl is veszi, éspedig az

y = 7 / 6

maximumot az

x = 69^{\circ} 18'

és

249^{\circ} 18'

, az

y = - 1 / 6

minimumot pedig az

x = 159^{\circ} 18'

és

339^{\circ} 18'

helyeken. (Tolnai Jenő)

III. megoldás. Írjuk a függvény (1) alakját a következőképpen:

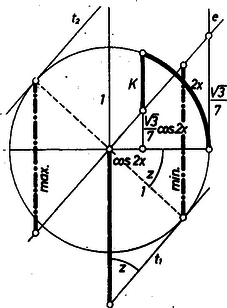
\begin{matrix} y = \frac{1}{2} + \frac{\sqrt[]{7}}{6} (sin 2 x - \frac{3}{\sqrt[]{7}} cos 2 x) . \end{matrix}

(5)

A függvény nyilván ugyanott veszi fel legnagyobb és legkisebb értékét, ahol a második tag, az pedig ugyanott, ahol a zárójelben levő

K

különbség. Egyszerűség kedvéért ezt ábrázoljuk a következő módon. Az egységnyi kerületű körre a

2 x

ívet felmérve,

sin 2 x

-et a szokásos módon ábrázoljuk. Ebből a ,,vízszintes'' egyenestől mérve

\frac{3}{\sqrt[]{7}} cos 2 x

szakaszt metsz le a középponton átmenő iránytangensű

e

egyenes. Így

K

-t az az előjeles ,,függőleges'' szakasz szemlélteti, amelynek végpontja a körre mért

2 x

ív végpontja, kezdő pontja pedig az

e

egyenesen van.

Meghúzva a kör

e

-vel párhuzamos

t_{1}

és

t_{2}

érintőjét,

K

nem nagyobb abszolút értékben, mint a

t_{1}

és

e

(vagy

t_{2}

és

e

) közti függőleges szakasz hossza, és éppen ekkora, pozitív, ill. negatív előjellel, ha a

2 x

ív végpontja az

e

-től pozitív irányban levő

t_{2}

, ill. a negatív irányban levő

t_{1}

érintési pontja.
Az érintési pontokba húzott sugár és a vízszintes közti

z

szögre

tg z = - \sqrt[]{7} / 3 = - 0, 8819

. Az ábra a

0^{\circ} \leq z < 360^{\circ}

, vagyis

0^{\circ} \leq x < 180^{\circ}

intervallumot öleli fel. Ebben a minimum

z = 2 x = 318^{\circ} 36'

-nél, vagyis

x = 159^{\circ} 18'

esetén adódik, a maximum helye pedig

z = 2 x = 138^{\circ} 36'

-ből

x = 69^{\circ} 18'

. A

t_{2}

és

e

függőlegesen mért távolsága

\begin{matrix} | \frac{1}{sin z} | = \frac{\sqrt[]{1 + {tg}^{2} z}}{| tg z |} = \frac{4}{\sqrt[]{7}}, \end{matrix}

ebből (5) alapján

\begin{matrix} y_{min} & = \frac{1}{2} + \frac{\sqrt[]{7}}{6} \cdot (- \frac{4}{\sqrt[]{7}}) = - \frac{1}{6} és \\ y_{max} & = \frac{1}{2} + \frac{\sqrt[]{7}}{6} \cdot \frac{4}{\sqrt[]{7}} = \frac{7}{6} . \end{matrix}