Kezdőlap


Feladat:	1574. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1968/november, 118 - 120. oldal		PDF \| MathML
Témakör(ök):	Beírt kör, Trapézok, Szögfüggvények, síkgeometriai számítások, Alakzatok köré írt kör, Feladat
Hivatkozás(ok):	Feladatok: 1967/december: 1574. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. a) A $C D M = H_{1}$ háromszög beírt körének $O_{1}$ középpontja rajta van $H_{1}$ és az $A B C D = T$ trapéz közös $f_{1}$ szimmetriatengelyén. $f_{1}$ átmegy a $T$ köré írható $k$ kör $O$ középpontján is, továbbá az $A$ pontot nem tartalmazó $C D$ ívet annak $F_{1}$ felezőpontjában metszi (1. ábra).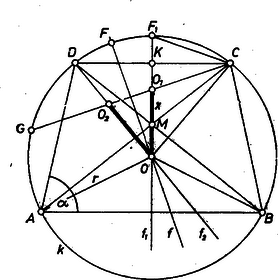

1. ábra

A C D = H_{2}

egyenlő szárú háromszög szimmetrikus

k

-nak

D

-ből kiinduló

f_{2}

átmérőjére, így

f_{2}

átmegy a

H_{2}

-be beírt kör

O_{2}

középpontján is.

f_{1}

és

f_{2}

szimmetrikusak a rövidebb

D F_{1}

ív

F

felezőpontján átmenő

f

átmérőre, hiszen

f

felezi az általuk bezárt szöget. Az

F_{1} C

ívet

f

-re tükrözve a

D G

ívet kapjuk, ahol a

B

-t nem tartalmazó

D G

és

D A

ívek egyirányúak, és

D G

egyenlő a

D A

ívvel egyenlő

C D

ív felével,

G

tehát felezi a

D A

ívet. Emiatt

C G

felezi a

H_{1}

és

H_{2}

háromszögek

C

csúcsnál levő közös szögét, és így átmegy az

O_{1}

O_{2}

pontokon. Az

f

-re tükrözve tehát az

f_{1}

és

C G

egyenesek

O_{1}

metszéspontja átmegy az

f_{2}

és

C G

egyenesek

O_{2}

metszéspontjába. Ebből ‐ mivel

f

átmegy

O

-n ‐ következik a bizonyítandó

O O_{1} = O O_{2}

egyenlőség.
b) Legyen

O_{1} O = x

O A = r

B A D ∢ = α

, és a

C D

oldal felezőpontja

K

. Ekkor

D O K ∢ = D O C ∢ / 2 = D O B ∢ / 4 = α / 2

, másrészt, mivel

F_{1} C D ∢ = D C G ∢ = F_{1} C O_{1} ∢ / 2

, ezért

K

O_{1} F_{1} = r - x

szakaszt is felezi; ennélfogva a

D O K

derékszögű háromszögből

\begin{matrix} cos \frac{α}{2} = cos D O K ∢ = \frac{O K}{O D} = \frac{O O_{1} + O_{1} K}{O D} = \frac{x + \frac{r - x}{2}}{r} = \frac{x + r}{2 r}, \end{matrix}

és innen

\begin{matrix} x = r (2 cos \frac{α}{2} - 1) . \end{matrix}

(1)

(Tusnády Gábor)

Megjegyzés. Nem kellett felhasználnunk, hogy

A B > C D

, ezért bizonyításunk

A B

és

C D

bármilyen nagyságviszonya esetén érvényes. Ugyanígy

x

kifejezése is, mert

C O D ∢ = A O D ∢ = B O C ∢ = α

, így a

C

-t tartalmazó

A O B

szög mértékszáma

3 α < 360^{\circ}

, ezért

α / 2 < 60^{\circ}

, tehát (1)-ben

r

szorzója pozitív.

II. megoldás. a) Tovább is a fenti jelöléseket használjuk, és

O_{1}

-et úgy tekintjük, mint a

H_{1}

-beli

C

és

D

szögek felezőinek metszéspontját,

O_{2}

-t pedig mint a

H_{2}

-beli

C

és

A

szögek felezőinek metszéspontját. Eszerint

D O_{1}

átmegy az

A

-t nem tartalmazó

B C

ív

L

felezőpontján,

A O_{2}

pedig

F_{1}

-en 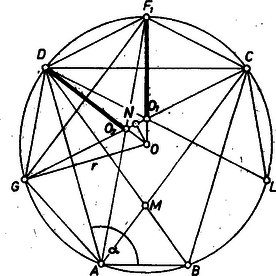(2. ábra).

2. ábra

A föltevések szerint a

C

-t tartalmazó

A B

ívet a

G

D

F_{1}

C

L

pontok egyenlő részekre osztják, emiatt az

A G D F_{1}

G D F_{1} C

D F_{1} C L

négyszögek egybevágó húrtrapézok, következésképpen

G D ∥ A F_{1}

D F_{1} ∥ G C

F_{1} C ∥ D L

. Így a

D G O_{2} F_{1}

és

D F_{1} C O_{1}

négyszögek egybevágó rombuszok, megfelelő átlóik egyenlők:

D O_{2} = F_{1} O_{1}

. Mindegyik átló meghosszabbítása átmegy

O

-n, mert pl. a

D O_{2}

egyenes a

G F_{1}

húr felező merőlegese, ezért a

D O

F_{1} O

sugarak további szakaszaira

O_{2} O = O_{1} O

, amit bizonyítanunk kellett.
b) A fentiek szerint az

O_{1} O_{2}

szakasz

N

felezőpontja egyszersmind

C G

-t is felezi, így az

O O_{2} N

és

O G N

derékszögű háromszögekből

\begin{matrix} x = O_{2} O = \frac{O N}{cos O_{2} O N ∢} = \frac{r cos G O N ∢}{cos O_{2} O N ∢} = r \frac{cos 3 α / 4}{cos α / 4} = r (4 cos^{2} α / 4 - 3) = r (2 cos α / 2 - 1) . \end{matrix}

(Felhasználtuk a bármely

β

szögre fennálló

cos 3 β = cos 2 β cos β - sin 2 β sin β = 4 cos^{3} β - 3 cos β,2 cos^{2} β = 1 + cos 2 β

azonosságokat, továbbá hogy

α / 4 < 30^{\circ}

, így

cos α / 4 \neq 0