Feladat: 1572. matematika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Csetényi Artúr ,  Csirmaz László ,  Ésik Zoltán ,  Fialovszky Alice ,  Gulyás András ,  Hárs László ,  Kardos János ,  Karvaly Gellért ,  Kele András ,  Kovalszky Róbert ,  Mihaletzky György ,  Munk Sándor ,  Nagy Dénes ,  Szilágyi Etelka ,  Zambó Péter 
Füzet: 1971/március, 103 - 106. oldal  PDF  |  MathML 
Témakör(ök): Bűvös-négyzetek, Számelrendezések, Négyzetrács geometriája, Számtani sorozat, Feladat
Hivatkozás(ok):Feladatok: 1967/december: 1572. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. A bélyegző az 1,2,...,n2 számok mindegyikét egyszer tartalmazza, így bármelyik számunknak a papíron való két előfordulása két különböző lenyomatba tartozik bele, tehát a két megfelelő mezőnek mind a soraihoz, mind az oszlopaihoz tartozó sorszámok különbsége az n számnak többszöröse (természetesen a 0-t is beleértve). Így ha a papírra egy n sorból és n oszlopból álló négyzet alakú keretet teszünk ‐ oldalaival a lenyomatok vonalaira ‐, akkor egyetlen szám sem látható kétszer a kereten belül, hiszen a keretbeli sorok, oszlopok sorszámai közti különbségek legnagyobbika n-1, ti. az alsó és felső sor, ill. a jobb szélső és a bal szélső oszlop sorszámai között. Nem lehet viszont, hogy számaink valamelyike ne forduljon elő a keretben. Ha ugyanis a számnak egy előfordulását megpróbáljuk kirekeszteni a keretből úgy, hogy ennek pl. a bal oldalvonalát áttoljuk rajta (a kirekesztendő szám mezejének jobb oldal vonalára), akkor a számnak n oszloppal jobbra levő előfordulása belép a keretbe a jobb oldali oldalvonalon át, és ugyanez áll a sorokra is.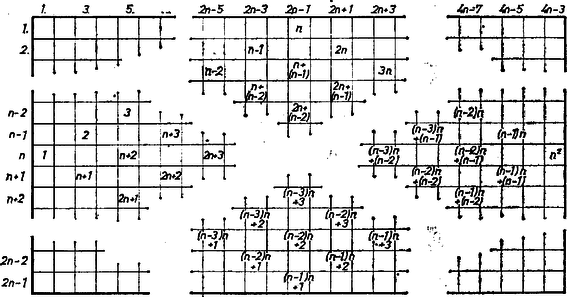

 
 
1. ábra
 
Megmutatjuk azt is, hogy a keretben látható n2 mező mindegyike egy és csak egy számot tartalmaz, a lenyomatok nem fedik át egymást, vagyis helyes ,,a papír megtöltött részéről'' beszélni.
Mivel a bélyegző sorainak száma 2n-1, azért egymásba csak olyan két lenyomat sorai nyúlhatnak, amelyek sorszámainak különbsége n. Elég annak a hatását tekinteni, ha az 1. lenyomathoz képest az alsó felét toljuk föl n sorral. Ekkora középső oszlop ‐ ti. az n,n+(n-1),...,(n-1)⋅n+1, számokat tartalmazó oszlop ‐ alsó felének számai üres közbülső mezőkre jutnak, mert az 1. lenyomat ezen oszlopában a mezők váltakozva foglaltak és üresek, a foglalt mezők sorának sorszámai (felülről értve) páratlanok, az üreseké párosak, a 2. lenyomatban viszont n-nel ‐ egy páratlan számmal ‐ kisebbek, tehát a 2. lenyomatbeli számok páros sorszámú sorba, azaz üres mezőre jutnak. Így pedig a 2. lenyomat többi számai sem juthatnak foglalt mezőkre, mert a foglalt mezők minden sorban 4 oszloponként követik egymást, és ennélfogva üres mezőtől jobbra és balra 4 oszloppal ismét üres mezőt találunk.
A fölhasznált állítások a beírási utasításból adódnak: egy számtól a bélyegzőn úgy jutunk el a közvetlen alatta levő számhoz ‐ amennyiben van alatta szám ‐, hogy egyszer balra lefelé és egyszer jobbra lefelé lépünk két oszloppal és egy sorral (és a két lépés sorrendje föl is cserélhető), tehát a közvetlen alatta levő szám két sorral lejjebb áll; azt is látjuk ebből, hogy a köztük levő sorbeli üres mezőtől balra és jobbra is üres áll, és a balra, jobbra második mezők foglaltak, oszlopaik sorszámának különbsége tehát 4.
Mindjárt itt megjegyezzük, hogy meggondolásunk szerint a bélyegzőn minden szám alatt 2 mezővel a nála (n-1)-gyel nagyobb szám áll, vagy üres mező, és minden számtól jobbra 4 mezővel az (n+1)-gyel nagyobb szám vagy üres mező, hiszen a jobbra emelkedő (balra süllyedő) lépés 1-gyel növel, ill. csökkent, a másik fajta lépés pedig n-nel.
Áttérve állításunknak a vízszintes eltolásokra vonatkozó részére, elég a 2n mezőnyi eltolásokkal foglalkoznunk, hiszen az 1. lenyomat csak páratlan sorszámú oszlopokba visz számokat, ezért az n mezővel jobbra eltolt lenyomat csak páros sorszámúakba és a foglaltság kérdése csak az újabb n mezővel jobbra való eltolás számaira lép fel. Mármost páratlan szám 2-szerese 4-gyel osztva maradékul 2-t ad, ott tehát üres mező van, hiszen csak olyan mező foglalt, amelyre az oszlopok sorszámainak különbsége 4-nek többszöröse, tehát 4-gyel osztva a maradék 0. Az 1. lenyomattól jobbra 4n mezővel képezve új lenyomatot, ez már nem nyúlik az elsőbe, mert a bélyegző oszlopainak száma csak 4n-3.
Ezzel beláttuk, hogy a lenyomatokat vízszintesen 2n, függőlegesen n többszöröseivel eltolva nincs átfedés, és ezzel megtöltjük a papír páratlan sorszámú oszlopait. Ugyanez áll egymás között azokra a lenyomatokra, amelyekben vízszintesen az n szám páratlan többszöröseit vesszük eltolásnak.
 

II. Áttérünk az összegek kérdésére. Legyen j olyan sorszám, amelyre 1≦j≦n ‐ vagyis a bélyegző j-edik sora a felső félben van, vagy maga a középső sor ‐, és számítsuk ki a bélyegző (felülről számított) j-edik és az n+j-edik sorában álló számok összegét, vagyis azokét a számokét, amelyek a papíron egy sorban állnak. Azt kell kapnunk, hogy ez független j-től.
A j-edik sor első száma n-(j-1), tagjainak száma j, és mint láttuk, tagról tagra (n+1)-gyel nőnek. Így összegük, a számtani sorozat összegképletét alkalmazva:
j2{2(n-j+1)+(j-1)(n+1)}.(1)

Az (n+j)-edik sor első száma 1+jn, tagjainak száma n-j, mert az n-edik sorban n szám áll (hiszen első száma 1, utolsó száma n2, és ehhez (n2-1):(n+1)=(n-1) lépéssel jutunk el) és tovább a sor sorszámát 1-gyel -1-gyel növelve a tagok száma 1-gyel -1-gyel fogy. (Innen is látjuk, hogy a vizsgált két sorban együttvéve n szám áll.) Így a (j+n)-edik sor számainak összege
n-j2{2(1+jn)+(n-j-1)(n+1)}
ami (1)-gyel együtt
n(n2+1)2,(2)
amint vártuk. (Ez j=n esetére is érvényes, mert ekkor ‐ bár nincs n+j-edik sor, de benne n-j, azaz 0 taggal számoltunk.)
Legyen másrészt k olyan páratlan sorszám, melyre 1≦k≦2n-1 ‐ vagyis a bélyegző k-adik oszlopa (az üres oszlopokat is számba véve) a bélyegző bal oldali felében van vagy maga a középső oszlop ‐, és számítsuk ki a bélyegző k-adik és (k+2n)-edik oszlopában álló ‐ a fentiek szerint a papíron egy oszlopba kerülő ‐ számok összegét.
A k-adik oszlop felső száma k+12 (egész), tagjainak száma ugyanennyi, a (k+2n)-edik oszlopra pedig ugyanezek a számok k+32⋅n, ill. 2n-k-12, tehát az összeg ‐ mint (n-1) differenciájú számtani sorozatok összege:
k+14{(k+1)+k-12(n-1)}+2n-k-14{(k+3)⋅n+2n-k-32(n-1)}==n(n2+1)2,


függetlenül k-tól és megegyezésben (2)-vel. Ezzel a bizonyítást befejeztük.
 

III. Az 1165. gyakorlatban Marci guruló bélyegzőjével azt a számkövezetet kaptuk ‐ lásd az ottani 2. ábrát ‐, ami az itteni pecsétnek egy oszlopra való tükrözésével állna elő n=5 esetében. Ott láttuk, hogy minden átlós összeg ‐ a keret elhelyezésétől függetlenül ‐ egyezik a sorok és az oszlopok összegével. Ugyanezt tapasztaljuk n=7 esetén (2. ábra), ebben a két esetben bélyegzőnk ún. minden átlójában bűvös ‐ az irodalomban bevett idegen kifejezéssel ‐ pándiagonális bűvös kövezetet állít elő.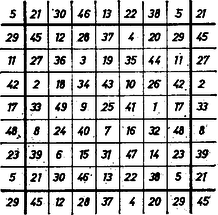
 
 
2. ábra
 

n=9 esetén mindkét átlós irány mentén csak 3-3 átlón annyi az összeg, mint a sorokon és oszlopokon, így a 81 szám közül 9 olyan, hogy a négyzet közepének választva bűvös négyzetet kapunk, ezek mellett a 3. ábrán csillag áll.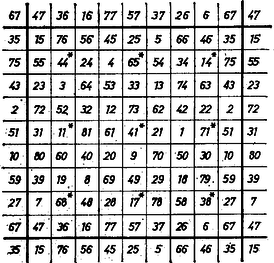
 
 
3. ábra
 

Megjegyzések. 1. A 2. és 3. ábrát úgy vágtuk ki a bűvös kövezetből, hogy a keret közepén a beírt számok közül a középső (n2+1)/2 álljon, a vonalak összegének n-edrésze. Ez azt eredményezte, hogy bármely két, a keret középpontjára tükrös helyzetű mezőpáron olyan két szám áll, amelyek összege n2+1, vagyis amelyek a beírt számok növekvő felsorolásában elölről és hátulról ugyanannyiadik helyen állnak.
2. A bélyegzőnk elvével keletkező kövezetnek pándiagonális voltáról lásd ezen számunk 97. oldalán olvasható cikket.