Feladat: 1569. matematika feladat Korcsoport: 14-15 Nehézségi fok: átlagos
Füzet: 1968/október, 58 - 60. oldal  PDF  |  MathML 
Témakör(ök): Egyenletrendszerek grafikus megoldása, Abszolútértékes egyenletrendszerek, Feladat
Hivatkozás(ok):Feladatok: 1967/december: 1569. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Grafikus megoldásban külön‐külön előállítjuk az (1), (2) egyenlet képét az x, y derékszögű koordinátarendszerben, majd leolvassuk a két kép közös pontjainak koordinátáit. Az abszolút érték nem negatív, így (1) bal oldalának egyik tagja sem nagyobb 6-nál, (2) bal oldalának tagjai pedig nem nagyobbak 4-nél.
Legyen x-1≧0, azaz 0≦x-1≦6, 1≦x≦7. Aszerint, hogy

x+y≧0,illetőlegx+y≦0,
(1) így alakul:
2x+y-7=0,ill.(x-1)-(x+y)-6=-y-7=0.
Az elsőből, x alsó és felső határának behelyettesítésével, x=1 esetén y=5, az x=7 esetben pedig y=-7, ennélfogva x-1≧0 mellett (1)-et a derékszögű koordinátarendszer
P1(1,5),P2(7,-7),P3(1,-7)
pontjai által határolt P1P2 és P2P3 szakaszának pontjai elégítik ki.
Hasonlóan x-1≦0, élesebben -5≦x≦1 eseté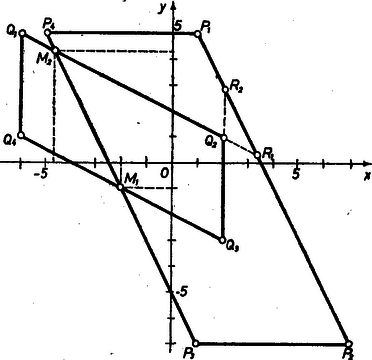n az
x+y≧0,illetőlegx+y≦0
további feltevés mellett az y=5, ill. y=-5-2x egyenletből a P4P1, ill. P3P4 szakaszt kapjuk, ahol P4(-5;-5). Ezek szerint (1) képe a P1P2P3P4 négyszög (ami nyilvánvalóan paralelogramma) kerülete.
 

 

Ugyanígy (2) képe a Q1Q2Q3Q4 paralelogramma kerülete, ahol Q1(-6,5), Q2(2,1), Q3(2,-3), Q4(-6,1), az oldalak rendre az x+2y-4=0, x=2, x+2y+4=0, x=-6 egyenletű egyenes részei. Ennélfogva az egyenletrendszer megoldásait a két paralelogramma kerületének két metszéspontjához tartozó koordináták adják:
M1-ből: x=-2,y=-1;M2-ből: x≈-4,7,y≈4,3.



 

II. Számítással úgy kereshetjük a megoldást, hogy az abszolút értékben levő kifejezések minden lehetséges előjelét tekintetbe vesszük és a kapott gyökökre megvizsgáljuk, teljesülnek-e ezek a feltételek. Ez az x+y<x+y+1 egyenlőtlenség figyelembevételével is 12 eset megvizsgálását kívánná. Csökkenthetjük azonban az esetek számát, ha először csak x-1 és y-1 előjelét vesszük figyelembe és minden esetben x+y=a-ra keresünk egyenletet.
a) x≧1, y≧1. Ebben az esetben x+y≧2, tehát mindegyik abszolútértékjelben pozitív szám áll:
2x+y=7,x+2y=7.
Az egyenletrendszer megoldása az R1(101,13) pont, nem tesz eleget az y≧1 feltételnek.
b) x≧1, y<1. Az ismert előjelű tagok abszolút értékét képezve az
|x+y|=7-x,|x+y+1|=3+y(3)


egyenletrendszert kapjuk. A másodikból kivonva az elsőt
|x+y+1|-|x+y=(x+y)-4.
Bevezetve az a=x+y jelölést, az
|a+1|-|a|=a-4
egyenletet kapjuk. A bal oldal értéke -1 és +1 között van, tehát a értéke csak a (3, 5) intervallumban lehet, a és a+1 tehát pozitív:
(a+1)-a=a-4.
Így a=x+y=5, ezt (3)-ba helyettesítve az R2 (2, 3) pontot kapjuk, de ez nem tesz eleget az y<1 feltételnek.
c) x<1, y≧1. Az ismert abszolút értékű tagok előjelét képezve
|x+y|=5+x,(4)|x+y+1|=5-y.


E két egyenlet különbsége az a=x+y jelöléssel az
|a|-|a+1|=a
egyenletre vezet: a bal oldal, és így a értéke is -1 és +1 között van, tehát a+1 értéke a (0, 2) intervallumban van, így előjele ismert:
|a|=2a+1.
a nem lehet pozitiv, mert akkor a=2a+1, tehát a<0; ezért 3a+1=0, a=-1/3. Ezt (4)-be helyettesítve az M2(-143,133) pontot kapjuk, mely eleget tesz feltevéseinknek, tehát megoldás.
d) x<1, y<1, a fentiekhez hasonlóan
|x+y|=5+x|x+y+1|=3+y.(5)


E két egyenlet összege az
|a|+|a+1|=a+8
egyenletre vezet, és mivel x+y<2, a<2. Ha -1≦a≦2, akkor a bal oldal legfeljebb 5, a jobb oldal legalább 7, így csak a<-1 lehet: -2a-1=a+8, tehát a=-3, és (5) alapján kapjuk a feltételeknek eleget tevő M1(-2,-1) pontot.