Kezdőlap


Feladat:	1565. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Berács J. , Draschitz R. , Farkas Gy. , Hárs L. , Jánossy D. , Kóczy L. , Kovalszky R. , Maróti P. , Mihaletzky György , Munk S. , Nagy András , Nagy Dénes , Papp Z. , Schván P. , Somogyi Á. , Váli L. , Váradi J. , Zsuppán F.
Füzet:	1968/november, 116 - 118. oldal		PDF \| MathML
Témakör(ök):	Pont körüli forgatás, Szinusztétel alkalmazása, Feladat, Síkgeometriai szerkesztések, Körök
Hivatkozás(ok):	Feladatok: 1967/november: 1565. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Bizonyításunk elvégzéséhez szükségünk lesz a következő egyszerű tényre: ha a $k_{1}$ és $k_{2}$ körök egymást az $M$ , $N$ pontokban metszik, és ezeken tetszőleges $m$ , ill., $n$ egyeneseket fektetünk át, amelyek a köröket másodszor rendre az $M_{1}$ , $M_{2}$ , ill., $N_{1}$ , $N_{2}$ pontokban metszik, akkor $M_{1} N_{1} ∥ M_{2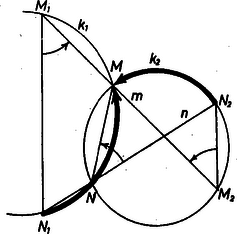} N_{2}$ (1. ábra)¹.

1. ábra

Valóban, az

N_{1} M_{1} M ∢ = N_{2} N M ∢ = N_{2} M_{2} M ∢

, tehát az

N_{1} M_{1}

N_{2} M_{2}

egyeneseket azonos forgatás viszi át az

M_{1} M_{2}

egyenesbe, így párhuzamosak.
Rátérünk a bizonyításra. Tükrözzük

Q

-t a feladatban szereplő

k

körnek az

E

ponton átmenő

e

átmérőjére, a kapott pontot jelöljük

Q'

-vel (2. ábr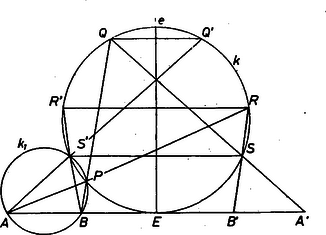a).

2. ábra

Messe az

A Q'

egyenes

k

-t az

S'

pontban: ez nyilván az

S

pont

e

-re vonatkozó tükörképe. Megmutatjuk, hogy az

A

B

P

S'

pontok egy

k_{1}

körön helyezkednek el. Ha

S'

és

P

azonosak, ez nyilvánvaló. Ha különbözők, legyen

k_{1}

B

P

S'

pontokon átmenő kör, és messe

k_{1}

-et a

Q' S'

egyenes

A^{*}

-ban. Fenti megjegyzésünk alapján

Q Q' ∥ B A^{*}

, és mivel

Q Q' ∥ E B

, így

A^{*}

B E

egyenesen is rajta van, tehát azonos a

B E

és

Q' S'

egyenesek metszéspontjával,

A

-val.

A

tehát rajta van

k_{1}

-en. Messe a

B S'

egyenes

k

-t másodszor

R'

-ben. Ugyancsak a fenti megjegyzés alapján

A B ∥ R' R

, tehát

R'

R

pont

e

-re vonatkozó tükörképe. Emiatt az

R' S'

egyenes

e

-re vonatkozó tükörképe az

R S

egyenes, és ez az

e

-re szimmetrikus

A E

egyenesből valóban a

B

pont

E

-re szimmetrikus

B'

párját metszi ki, amit bizonyítanunk kellett.
(Tusnády Gábor)

Megjegyzések. 1. Bizonyításunk független attól, hogy

Q

és

R'

közül melyik van közelebb az

A A'

egyeneshez. Nem használtuk ki sem az

E B < E A

B P < B Q

nagyságviszonyokat, sem azt, hogy

B

ugyanazon oldalán van

E

-nek, mint

A

, tehát a szerkesztés e korlátozások nélkül érvényes. Ajánljuk az olvasóknak ezek átgondolását.
2. Hasonlóan szerkeszthető (és a szerkesztés helyessége hasonlóan bizonyítható) a

k

kör

e

átmérőjének tetszőleges

E

pontjában emelt merőleges egyenes tetszőleges

B

pontjának

E

-re vonatkozó

B'

tükörképe, ha adott az egyenesen az

E

-re szimmetrikus

A

A'

pontpár (3. ábra). Ha a szerkesztés vagy a bizonyítás során két pont azonosnak adódik a

k

körön, az általuk meghatározott egyenesnek a

k

kör e közös ponthoz tartozó érintőjét tekintjük. Ilyen esetben a bevezetőben megoldott segédfeladatban is meg kell engednünk, hogy az

m

n

egyenesek a

k_{1}

k_{2}

körök érintői legyenek. (T. G.)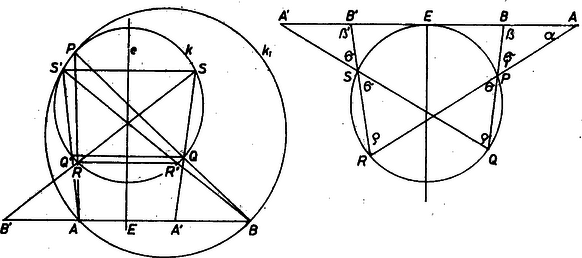

3. ábra 4. ábra

Sokan számítással bizonyították az állítást. Ilyen a következő

II. megoldás. Használjuk a 4. ábra szögjelöléseit. Az egyenlően jelölt szögek nyilvánvalóan egyenlők. A

B' A' S

háromszögből a színusz tétel alapján

\begin{matrix} A' B' = A' S \cdot \frac{sin σ}{sin β'} = A' S \cdot \frac{sin A P B ∢}{sin A B' R ∢} . \end{matrix}

(1)

Alkalmazzuk a körhöz húzott szelő és érintő tételét az

A'

, majd az

A

pontra, továbbá a színusz tételt az

A B P

és

A B' R

háromszögnek (1)-ben szereplő alkotórészére:

\begin{matrix} A' S = \frac{A' E^{2}}{A' Q} = \frac{A E^{2}}{A' Q} = \frac{A P \cdot A R}{A' Q}, \\ sin A P B ∢ = \frac{A B sin A B P ∢}{A P} = \frac{A B sin A' B Q ∢}{A P}, \\ \frac{1}{sin A B' R ∢} = \frac{B' A}{A R sin A R B' ∢} = \frac{B' A}{A R sin A' Q B ∢} . \end{matrix}

Ezeket összeszorozva

\begin{matrix} A' B' = \frac{A B \cdot B' A}{\frac{A' Q sin A' Q B ∢}{sin A' B Q ∢}}, \end{matrix}

és felismerjük, hogy a nevezőben az

A' Q B

háromszög

B A'

oldala áll. Átrendezéssel, majd mindkét oldalhoz 1-et adva

\begin{matrix} \frac{A' B'}{B' A} = \frac{A B}{B A'}, \frac{A' A}{B' A} = \frac{A A'}{B A'}, \end{matrix}

eszerint

B' A = B A'

, és ez az állítást igazolja.
Michaletzky György (Budapest, Piarista Gimn., III. o. t.)

¹Lásd: Czapáry Endre-Horvay Katalin-Reiman István-dr. Soós Paula: Geometriai feladatok gyűjteménye, Tankönyvkiadó, Budapest, 1964, 872. feladat, 55. o.