Feladat: 1559. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Berács József ,  Siklósi István 
Füzet: 1968/szeptember, 16 - 17. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Tengelyes tükrözés, Szinusztétel alkalmazása, Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):Feladatok: 1967/október: 1559. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. (1) így alakítható:

AB:AC=AD:(AC+AD).(2)
Mérjük rá az AD átlót AC-nek C-n túli meghosszabbítására, s legyen a végpont V. Ekkor
AV=AC+CV=AC+AD,
a (2) aránypár utolsó tagja. Mivel másrészt BAC∢=DAC∢, azért (2) miatt ABC és ADV hasonló háromszögek. Ámde az elsőben BC=AC, emiatt a másodikban DV=DA=CV, tehát CDV is egyenlő szárú háromszög, továbbá CVD∢=CAD∢.
Eszerint V-nek a CD egyenesre való U tükörképe rajta van a kérdéses S sokszög köré írt k körön, éspedig S-nek az ABCD... körüljárást folytatva utolsó csúcsa, hiszen a tükrözés miatt a CVDU négyszög rombusz; UD a k-nak AC-vel párhuzamos húrja, tehát AU=CD, mint párhuzamos húrok közti ívekhez tartozó húrok. Továbbá DU=CV=DA, tehát az AU sokszögoldal f felező merőlegese átmegy D-n és k középpontján. Így az ABCD töröttvonalat f-re tükrözve az A csúcs U-ba megy át, D helyén marad, a B, C csúcsok pedig S hiányzó csúcsaiba mennek át. Előállítottuk tehát S összes csúcsát, 7 csúcsot kaptunk, S oldalainak a száma tehát csak 7 lehet. A fentiek alapján az is világos, hogy a szabályos 7-szög eleget tesz (1)-nek.
Berács József (Győr, Czuczor G. Gimn., IV. o. t.)

dolgozata elindulásából, a szög-számítások kiküszöbölésével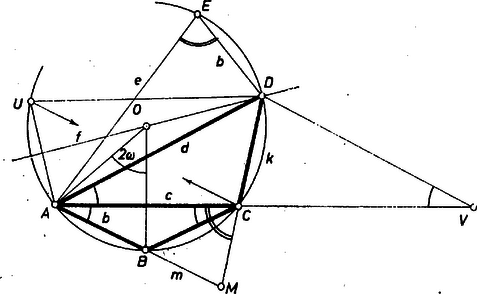

 

 

II. megoldás. Legyen az S sokszög oldalainak száma n. A feladatban 4 csúcsról van szó, tehát n≥4. Szabályos négyszögre AB=AD, (1) tehát nem teljesülhet, így n>4. Legyen S-nek D után következő csúcsa E, az AB és CD egyenesek metszéspontja M (n>4 miatt M létezik); és jelöljük az AB, AC, AD, AE szakaszok hosszát rendre b, c, d, e-vel. Mivel S szimmetrikus BC felező merőlegesére, az MBC háromszög egyenlő szárú: MB=MC=m. Az AMC és ADE háromszögek A-nál levő szögei egyenlő húrokhoz tartozó kerületi szögek, az ACM szög az ACDE húrnégyszög külső szöge, így egyenlő az AED szöggel, tehát az AMC és ADE háromszögek hasonlók. Így egyrészt AM:MC=AD:DE, másrészt MC:AC=DE:AE, azaz
 
(b+m):m=d:b,m:c=b:e.
 


Az elsőből bm=db-1, így a másodikból
e=cbm=c(db-1)=cd(1b-1d).(3)

Megjegyezzük, hogy eddig nem használtuk fel (1)-et, a kapott összefüggés tetszőleges n>4 esetén érvényes. Jelöléseinkkel (1) alapján a zárójelben 1/c áll, tehát e=d. Így ADE egyenlő szárú háromszög. ‐ A megoldás befejezése azonos a fentebbivel.
Siklósi István (Budapest, Berzsenyi D. Gimn., IV. o. t.)
 

Megjegyzés. Megoldásunk trigonometriai megfelelője a következő.
Legyen S középpontja O, a köréje írt kör átmérője 1, és AOB∢=2ω. Ekkor b=sinω, c=sin2ω,d=sin3ω,e=sin4ω, igy (1) az
1sinω=1sin2ω+1sin3ω.(4)
egyenletre vezet. Megoldásához a (3) azonosságnak megfelelő
sin4ω=sin2ωsin3ω(1sinω-1sin3ω)(5)
azonosságot használjuk fel. Ez egyébként önállóan is igazolható: beszorozva és átrendezve a
sin4ω+sin2ω=2cosωsin3ω
azonosságot kapjuk, ez pedig a két szög színusza összegének szorzattá alakítására ismert azonosság alapján. helyes.
Mármost (5) alapján (4) a sin4ω=sin3ω egyenletre vezet. A feladat szerint, feltéve, hogy S konvex sokszög, 0<3ω<4ω<180∘, így 3ω és 4ω kiegészítő szögek: összegük 180∘,ω=180∘7, tehát S oldalainak száma 7.