Kezdőlap


Feladat:	1557. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Sax Gyula
Füzet:	1968/november, 110 - 111. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Geometriai egyenlőtlenségek, Terület, felszín, Paralelogrammák, Feladat
Hivatkozás(ok):	Feladatok: 1967/október: 1557. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az $A$ és $C$ csúcs, továbbá az eltolódó $E F$ egyenes távolsága a $B D$ átló egyenesétől rendre $m_{a}$ , $m_{c}$ , $x$ . $C E F$ és $C B D$ hasonló háromszögek, ebből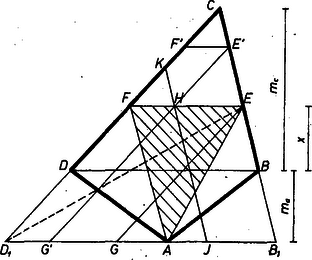

\begin{matrix} E F = B D \cdot \frac{m_{c} - x}{m_{c}}, \end{matrix}

így az

A E F

háromszög területe, mint

x

függvénye:

\begin{matrix} y = \frac{B D}{2 m_{c}} (m_{c} - x) (m_{a} + x) = - \frac{B D}{2 m_{c}} (x + m_{a}) (x - m_{c}), \end{matrix}

ahol

0 \leq x \leq m_{c}

.
Ez másodfokú függvény. Jól tudjuk, hogy minden (valódi) másodfokú függvénynek van szélső értéke, és annak helyét megadja a függvény két

0

-helyének számtani közepe, ill. bármely olyan

x'

x''

helyek számtani közepe, amely helyeken a függvény egyenlő értéket vesz fel. Esetünkben a

0

-helyek

x = - m_{a}

és

x = m_{c}

, tehát a szélső érték helye

\begin{matrix} x_{0} = \frac{m_{c} - m_{a}}{2}, \end{matrix}

amennyiben ez a hely beletartozik az értelmezési tartományba:

\begin{matrix} 0 \leq x_{0} \leq m_{c}, azaz 0 \leq \frac{m_{c} - m_{a}}{2} = m_{c}, vagyis ha m_{a} \leq m_{c} . \end{matrix}

Ez akkor teljesül, ha

C

távolabb van a

B D

átlótól, vagy legalább ugyanannyira van tőle, mint az

A

csúcs.
Azt is tudjuk, hogy a másodfokú függvénynek maximuma, ill. minimuma van aszerint, hogy egy a mondott

x'

x''

helyek közti helyen nagyobb, ill. kisebb értéket vesz fel, mint a két helyen felvett közös érték. Mármost

- m_{a} < 0 < m_{c}

, és az

x = 0

helyen függvényünk értéke

\begin{matrix} y = \frac{B D \cdot m_{a}}{2} > 0, \end{matrix}

tehát

x_{0}

-ban maximum van, ha

m_{a} \leq m_{c}

.
Ha

x_{0} < 0

, azaz

m_{a} > m_{c}

, akkor hasonló meggondolás szerint a

0 \leq x \leq m_{c}

intervallumban a függvény monoton csökken, legnagyobb értékét az intervallum bal végpontjában,

x = 0

-ban veszi fel, ekkor az eltolódás folyamán az

A E F

háromszög a kiinduló

A B D

helyzetben vesz fel legnagyobb területet. ‐ Más vizsgálandó eset nincs, mert

x_{0} > m_{c}

lehetetlen.

Sax Gyula (Budapest, Kölcsey F. G., III. o. t.)

II. megoldás. Messe az

A

-n át

B D

-vel párhuzamosan húzott egyenes

C B

és

C D

meghosszabbítását a

B_{1}

, ill.

D_{1}

pontban. Ekkor az

A E F

háromszög területe egyenlő a

D_{1} E F

háromszögével és fele akkora, mint a

D_{1} G E F = P

paralelogrammáé, ‐

G

-vel jelölve az

E

-n át

C D_{1}

-gyel párhuzamosan húzott egyenes metszéspontját

B_{1} D_{1}

-gyel. Elég tehát a

B D

-vel párhuzamos egyenesek különböző helyzeteihez tartozó ilyen paralelogrammák közül keresni ki a legnagyobb területűt.
Az egyenes egy

C

-hez közelebbi helyzetéhez tartozó, megfelelő paralelogramma legyen

D_{1} G' E' F' = P'

E F

és

E' G'

metszéspontja pedig

H

. Ekkor

P'

-ből az

E' F' F H

paralelogramma nyúlik túl

P

-n, viszont az utóbbiból

E H G' G

-t nem fedi le

P'

. Hasonlítsuk össze e két paralelogramma területét. Toljuk el

G' G

-t

D_{1} B_{1}

-en a

J B_{1}

helyzetbe,

F F'

-t pedig

D_{1} C

-n a

K C

helyzetbe. Ismét paralelogrammákat kapunk, tehát

H

J

K

egy a

B_{1} C

-vel párhuzamos egyenesen van.

P'

területe

C K H E'

területével nagyobb, viszont

B_{1} E H J

területével kisebb, mint

P

területe. Az említett két paralelogrammának a

B_{1} C

egyenesre merőleges magassága egyenlő, így az első aszerint kisebb területű a másodiknál, egyenlő vele, vagy nagyobb nála, amint

C E'

kisebb

B_{1} E

-nél, egyenlő vele, vagy nagyobb nála, ez pedig attól függ, hogy

E' F'

messzebb van-e

C

-től, mint

E F

A

-tól, vagy ugyanakkora távolságra vannak, vagy

E F

van közelebb

A

-hoz mint

E' F'

C

-hez. Ugyanezt mondhatjuk tehát a

P'

P

paralelogrammák és az

A E' F'

A E F

háromszögek területéről is.
Eszerint a

C

csúcsból indítva a

B D

-vel párhuzamos egyenest, az

A E F

háromszög területe nő, míg el nem éri az egyenes

B D

-t, ha ez

C

-től legfeljebb akkora távolságra van, mint

A

-tól; ha viszont

A

-hoz van közelebb, akkor addig növekszik a háromszög területe, míg az egyenes egyenlő távolságra nem lesz

C

-től és

A

-tól; tovább közeledve

A

-hoz a terület csökken. A legnagyobb területet tehát a

B D

átló szolgáltatja, ha ez

C

-től legfeljebb akkora távolságra van, mint

A

-tól, viszont a két mondott csúcstól egyenlő távolságra levő egyenes, ha

B D

közelebb van

A

-hoz, mint

C

-hez.