Kezdőlap


Feladat:	1548. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1968/november, 105 - 108. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Geometriai egyenlőtlenségek, Terület, felszín, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1967/szeptember: 1548. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Egy az előírásoknak megfelelő $A B C$ háromszöget a következő lépésekben keresünk. 1. Az $A_{0} B_{0} C_{0} = H_{0}$ háromszög $A_{0} B_{0}$ és $B_{0} C_{0}$ oldala fölé, kifelé megszerkesztjük az $A' C' B' ∢ = γ$ , ill. $B' A' C' ∢ = α$ nyílású $i_{c}$ , ill. $i_{a}$ látószög körívet ‐ ezen kell lennie a $C$ , ill. $A$ csúcsnak; 2. $B_{0}$ -on át olyan egyenest veszünk fel, mely mindkét ívet metszi egy-egy belső pontjukban ‐ és így természetesen kívül halad $H_{0}$ -on ‐, legyen a metszéspont $C$ , ill. $A$ ; 3. megkeressük a $C A_{0}$ és $A C_{0}$ egyenesek $B$ metszéspontját.
Az így szerkesztett $A B C = H$ háromszögben $C$ -nél $γ$ , $A$ -nál $α$ nagyságú szög van, tehát $A B C ▵ \sim A' B' C' ▵$ , csúcsaik a felsorolás rendjében felelnek meg egymásnak, és az $A B$ , $B C$ , $C A$ egyenesek rendre átmennek a $C_{0}$ , $A_{0}$ , $B_{0}$ ponton.
Megjegyezzük, hogy a mondott $B$ pont mindig azon a $k_{b}$ körön adódik, amelynek $A_{0} C_{0}$ húrja, és $B_{0}$ -lal ellentétes oldalon levő $i_{b}$ ívének pontjaiból a húr $A' B' C' ∢ = β$ szögben látszik. Ha ugyanis az adódó $H$ tartalmazza $H_{0}$ -t, akkor $B$ az $A_{0} C_{0}$ egyenes $B_{0}$ -t nem tartalmazó partján van, és belőle az $A_{0} C_{0}$ szakasz $β$ szögben látszik; ha pedig $H$ nem tartalmazza $H_{0}$ -t, mert $B$ az $A_{0} C_{0}$ egyenesnek $B_{0}$ -t tartalmazó partján adódott ‐ lásd az ábra $\bar{A} \bar{B} \bar{C}$ háromszögét, $C_{0}$ nincs rajta az $\bar{A} \bar{B}$ szakaszon, $\bar{B} \bar{C}$ átmetszi $H_{0}$ -t, akkor $B$ -ből az $A_{0} C_{0}$ szakasz $180^{\circ} - β$ szögben látszik, és ezért van rajta $k_{b}$ -n.
Az $\bar{A} \bar{B} \bar{C}$ háromszögben látott példára tekintettel megmutatjuk, hogy mindig felvehető $B_{0}$ -n át olyan egyenes, hogy a belőle szerkesztett $A B C$ háromszög valódi körülírt háromszöge az $A_{0} B_{0} C_{0}$ háromszögnek. Ilyen a $B_{0}$ -on átmenő, $A_{0} C_{0}$ -lal párhuzamos egyenes. Ekkor ugyanis az $A_{0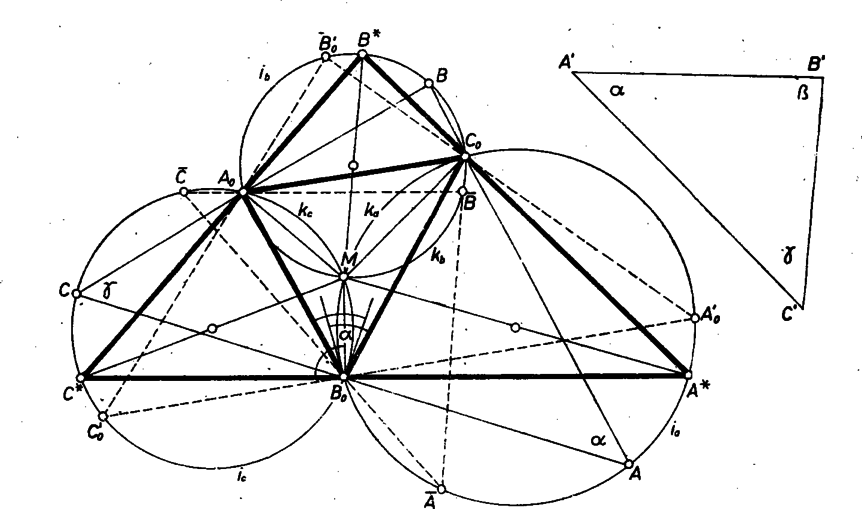} C$ , $C_{0} A$ félegyenesek az $A_{0} C_{0}$ egyenes $B_{0}$ -t tartalmazó oldalán vannak, az $A_{0} C_{0}$ szakasszal bezárt szögük rendre $180^{\circ} - γ$ , $180^{\circ} - α$ , ezek összege $180^{\circ} + β > 180^{\circ}$ , ezért a két félegyenes nem metszi egymást, csak visszafelé való meghosszabbításaik, tehát $B$ az $A_{0} C_{0}$ egyenes $B_{0}$ -t nem tartalmazó oldalán adódik, és $H$ a belsejében tartalmazza $H_{0}$ -t.

II. Azt is kaptuk, hogy tetszés szerinti számú, a követelményeknek megfelelő

H

háromszög szerkeszthető. Ezek egymáshoz is hasonlók, tehát közülük az a legnagyobb területű, amelyikben pl. a

C A

oldal hossza a legnagyobb.
Tekintsük az

i_{a}

és

i_{c}

íveket tartalmazó

k_{a}

k_{c}

körök

B_{0}

-tól különböző

M

metszéspontját. Ez mindkét ívnek a kiegészítő ívén, az

A_{0} B_{0} C_{0}

szögtartományban van, mert a körök

B_{0}

-beli érintői a

B_{0} C_{0}

B_{0} A_{0}

egyenessel rendre

α

γ

szöget zárnak be és e két szög átfedi egymást, mert a feltevés alapján

\begin{matrix} α + β = 180^{\circ} - γ > 90^{\circ} > β_{0} = A_{0} B_{0} C_{0} ∢ \end{matrix}

Ennélfogva

C

-nek

i_{c}

-n való mozgása közben az

M C B_{0}

szög állandó, és ugyanez áll az

M A B_{0}

szögre. Így pedig,

H

-t változtatva, az

M

-ben közös csúccsal bíró

M A C

háromszögek is hasonlók, és

C A

akkor a legnagyobb, ha

M C

a legnagyobb, vagyis ha

C

k_{c}

-nek

M

-mel átellenes

C^{*}

pontjában van.
Ezzel eljárást kaptunk a keresett legnagyobb területű

A^{*} B^{*} C^{*} = H^{*}

háromszög megszerkesztésére: a

C^{*} B_{0}

egyenes

k_{a}

-ból kimetszi

A^{*}

-ot, és a

C^{*} A_{0}

A^{*} C_{0}

egyenespár metszéspontja

B^{*}

H^{*}

megfelel az előbbi előírásoknak is, mert az

M B_{0} C^{*}

szög derékszög, tehát az

M B_{0} A^{*}

szög is

90^{\circ}

. Így

C^{*}

i_{c}

-n,

A^{*}

i_{a}

-n van, hiszen

γ

és

α

hegyesszögek, az ívek nagyobbak félkörnél. Hasonlóan a

B^{*} C^{*}

B^{*} A^{*}

oldalszakasz tartalmazza

A_{0}

-t, ill.

C_{0}

-t. Ennek bizonyításához felhasználjuk, hogy ‐ mint láttuk ‐

B

k_{b}

-n van, továbbá hogy

k_{b}

is átmegy

M

-en. Valóban, mint láttuk,

\begin{matrix} A_{0} M B_{0} ∢ = 180^{\circ} - γ > 90^{\circ}, B_{0} M C_{0} ∢ = 180^{\circ} - α > 90^{\circ}, \end{matrix}

ezért összegük

180^{\circ}

és

360^{\circ}

közé esik,

M

benne van

H_{0}

-ban, és

C_{0} M A_{0} ∢ = 180^{\circ} - β

, tehát

M

i_{b}

-t kiegészítő ív pontja. Ekkor pedig

A^{*} C_{0} M ∢ = 90^{\circ}

miatt

M C_{0} B^{*} ∢ = 90^{\circ}

, tehát

B^{*}

k_{b}

-nek

M

-mel átellenes pontja.

Megjegyzés.

H_{0}

hegyesszögű voltának felhasználása nélkül is belátható, hogy mindig húzható

B_{0}

-on át olyan

A C

egyenes, hogy a belőle kapott

H

háromszög valódi körülirt háromszöge

H_{0}

-nak.
Válasszunk egy alapirányt, járjuk körül

H_{0}

-t és

H

-t, és írjuk fel mindegyik oldaluknak mint félegyenesnek az irányszögét, vagyis azt, mekkora elfordulás viszi át az alapirányt az illető félegyenesbe, majd ezekből annak feltételeit, hogy

H

-nak mindhárom oldalegyenese

H_{0}

-on kívül haladjon.
Feltehetjük, hogy

H_{0}

körüljárása pozitív, hiszen ezt ‐ ha kell ‐ két csúcs betűzésének fölcserélésével elérhetjük. Így

H

körüljárása is pozitív lesz, és az irányszög minden egyes csúcson áthaladva, az illető csúcsnál levő külső szöggel nő.
Legyen az alapirány az

A_{0} B_{0}

félegyenes iránya, legyenek továbbá

H_{0}

egymás utáni szögei

α_{0}

β_{0}

γ_{0}

végül a

C A

félegyenes irányszöge

φ

. Így az irányszögek:

\begin{matrix} A_{0} B_{0} & : 0^{\circ} (ill. egyszeri körüljárás után 360^{\circ}), \\ B_{0} C_{0} & : 180^{\circ} - β_{0}, \\ C_{0} A_{0} & : (180^{\circ} - β_{0}) + (180^{\circ} - γ_{0}) = 180^{\circ} + α_{0}, \\ C A & : φ, \\ A B & : φ + 180^{\circ} - α, \\ B C & : (φ + 180^{\circ} - α) + (180^{\circ} - β) = φ + 180^{\circ} + γ . \end{matrix}

C A

félegyenes

H_{0}

-on kívül halad, ha irányszöge

A_{0} B_{0}

és

B_{0} C_{0}

irányszöge közé esik:

\begin{matrix} 0^{\circ} < φ < 180^{\circ} - β_{0}; \end{matrix}

(1)

Hasonlóan az

A B

B C

félegyenesből

\begin{matrix} 180^{\circ} - β_{0} < φ + 180^{\circ} - α < 180^{\circ} + α_{0}, 180^{\circ} + α_{0} < φ + 180^{\circ} + γ < 360^{\circ}, \end{matrix}

azaz

φ

-re megoldva

\begin{matrix} α - β_{0} < φ < α + α_{0}, & (2) \\ α_{0} - γ < φ < 180^{\circ} - γ . & (3) \end{matrix}

Mármost

φ

-nek bármelyik kapott felső korlátjából bármelyik másik kettős egyenlőtlenségbeli alsó korlátját kivonva pozitív különbséget kapunk, ugyanis a

6

különbség így alakítható:

\begin{matrix} 180^{\circ} - α, 180^{\circ} - β, 180^{\circ} - γ; α_{0} + α, β_{0} + β, γ_{0} + γ, \end{matrix}

ennélfogva a felső korlátok legkisebbike nagyobb az alsó korlátok legnagyobbikánál. Így pedig van az (1)‐(3)-nak eleget tevő

φ

irányszög; ezt akartuk belátni. Tetszés szerinti

H_{0}

H

háromszög-pár esetén adódhat az

α_{0} > 180^{\circ} - γ

nagyságviszony; ekkor a hegyesszögek esetére fönt ajánlott

φ = α_{0}

irányszögű egyenes nem felelne meg.