Kezdőlap


Feladat:	1544. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bajmóczy Ervin , Balogh J. , Berács J. , Bodor I. , Bulkai T. , Csörgei J. , Erdődi György , Katona V. , Körmendi S. , Lakatos L. , Lempert L. , Losonci Z. , Lublóy L. , Moson P. , Nagy Zs. , Péli Katalin , Perémy G. , Pintz J. , Siklósi I. , Somos E. , Szabó Klára , Takács L. , Tátray P. , Zambó Péter
Füzet:	1968/március, 107 - 109. oldal		PDF \| MathML
Témakör(ök):	Szabályos sokszög alapú gúlák, Térfogat, Szabályos testek, Feladat
Hivatkozás(ok):	Feladatok: 1967/május: 1544. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) Az 1472. feladatban vizsgált $I$ szabályos ikoszaédernek $20$ szabályos háromszöglapja van, egységnyi oldalakkal, a szerkesztésben felhasznált $B_{1} B_{2} B_{3} B_{4} B_{5}$ és $C_{1} C_{2} C_{3} C_{4} C_{5}$ ötszögek mindegyik oldalában $2 - 2$ háromszög fut össze ( $A$ és a $C$ csúcsok felé, ill. $D$ és a $B$ csúcsok felé), és ezzel minden lapot egyszer vettünk számba.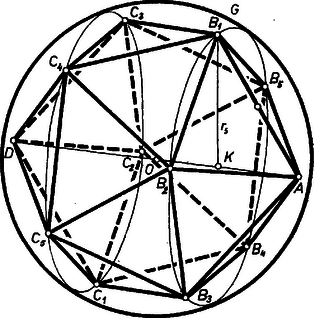

Térfogatának kiszámításához szétvágjuk a testet mindazon háromszögek mentén, melyeknek egyik oldala a testnek egy éle, ezzel szemben fekvő csúcsa pedig a test köré írt

G

gömbnek

O

középpontja. Így

I

szétesik

20

háromoldalú gúlára. E gúlák egybevágók, hiszen ez áll alapháromszögeikre, másrészt oldallapjaikra is, amelyek egyenlő szárú háromszögek, száruk

G

-nek

r

sugarával egyenlő. A gúlák magassága annyi, mint

I

bármelyik lapjának

O

-tól való

d

távolsága. Ezt abból számíthatjuk, hogy az

I

lapjai köré írt körök egyszersmind

G

-nek síkmetszetei, és sugaruk az egységnyi oldalú szabályos háromszög magasságának

2 / 3

része:

r_{3} = (\sqrt[]{3} / 2) \cdot (2 / 3) = 1 / \sqrt[]{3}

, másrészt hogy az idézett feladat szerint

\begin{matrix} r = \sqrt[]{\frac{5 + \sqrt[]{5}}{8}}, tehát d^{2} = r^{2} - r_{3}^{2} = \frac{5 + \sqrt[]{5}}{8} - \frac{1}{3} = \frac{14 + 6 \sqrt[]{5}}{48} = \frac{1}{3} {(\frac{3 + \sqrt[]{5}}{4})}^{2}, \end{matrix}

ennélfogva az ikoszaéder térfogata

\begin{matrix} V = 20 \cdot \frac{1}{3} \cdot \frac{\sqrt[]{3}}{4} \cdot \frac{1}{\sqrt[]{3}} \cdot \frac{3 + \sqrt[]{5}}{4} = \frac{5 (3 + \sqrt[]{5})}{12} (\approx 2,18) \end{matrix}

térfogategység (a térfogategységnyi kocka éle egyenlő

I

élével).
b) Az 1440. feladathoz fűzött megjegyzés szerint a tv-labda előállítható a szabályos ikoszaéderből úgy, hogy ennek mindegyik élét

3

egyenlő részre osztjuk, mindegyik csúcsból kiinduló

5

él közelebbi harmadoló pontjain át síkot fektetünk, és eltávolítjuk a testről azt a szabályos ötoldalú gúlát, amely így a síknak

O

-t nem tartalmazó oldalán keletkezett.

5

ilyen pont valóban mindig egy síkban van, mert pl. az

A

-ból kiinduló élek végpontjai a

B_{1} B_{2} B_{3} B_{4} B_{5} =

Ö (síkbeli) ötszöget alkotják, a mondott

5

pont pedig ennek

1 / 3

arányú kicsinyített képe,

A

-ból mint hasonlósági középpontból, tehát rajta van azon a síkon, amely

Ö

síkjával párhuzamos és átmegy az

A K

szakasz

A

-hoz közelebbi harmadoló pontján.
Vegyük hosszúságegységnek a tv-labda élét, ekkor

3

egységnyi élű ikoszaéderből kell kiindulnunk, ennek térfogata

27 V

, ahol

V

az a) részben kapott térfogat.
A lemetszett gúla ekkor egybevágó az 1472. feladatbeli

A Ö

gúlával. Ezt az

A K B_{i}

háromszögek mentén

(i = 1

2

3

4

5

)

5

egybevágó háromoldalú gúlára daraboljuk. Az idézett feladat szerint közös magasságuk, valamint az

Ö

köré írt kör

r_{5}

sugara, a

K B_{i} B_{i + 1}

egyenlő szárú háromszög szára

\begin{matrix} m = A K = (1 - \frac{1}{\sqrt[]{5}}) r = \sqrt[]{\frac{5 - \sqrt[]{5}}{10}}, r_{5} = B_{i} K = \frac{2}{\sqrt[]{5}} r = \sqrt[]{\frac{5 + \sqrt[]{5}}{10}}, \end{matrix}

így e háromszögek

m_{5}

magasságára

\begin{matrix} m_{5}^{2} = r_{5}^{2} - {(\frac{1}{2})}^{2} = \frac{5 + 2 \sqrt[]{5}}{20}, \end{matrix}

ennélfogva az

A Ö

gúla térfogata:

\begin{matrix} V_{g} = 5 \cdot \frac{1}{2} m_{5} \cdot \frac{m}{3} = \frac{5}{6} \cdot \sqrt[]{\frac{(5 + 2 \sqrt[]{5}) (5 - \sqrt[]{5})}{200}} = \frac{\sqrt[]{30 + 10 \sqrt[]{5}}}{24} = \frac{5 + \sqrt[]{5}}{24} . \end{matrix}

Az ikoszaédernek

12

csúcsa van, így a tv-labda térfogata

\begin{matrix} 27 V - 12 V_{g} = \frac{135 + 45 \sqrt[]{5}}{4} - \frac{5 + \sqrt[]{5}}{2} = \frac{125 + 43 \sqrt[]{5}}{4} (\approx 55, 3 térfogategység) . \end{matrix}

Erdődi György (Szeged, Rózsa F. g. III. o. t.)
Bajmóczy Ervin (Budapest, Ady E. Ált. Isk. 8. o. t.)

Megjegyzések. 1.

V_{g}

-t megkapjuk abból is, hogy vesszük azt az

5

gúlát, amely

I

térfogatának számításában az

A Ö

gúla oldallapjain áll, és közös negyedik csúcsuk

O

. Ez

Ö

alapú kettős gúla, és két része térfogatainak aránya

K A : K O

, ami a szabályos ötszög szerkesztése szerint

(\sqrt[]{5} - 1) : 1

. A kettős gúla térfogata

V / 4

, így

\begin{matrix} v_{g} = \frac{V}{4} \cdot \frac{\sqrt[]{5} - 1}{(\sqrt[]{5} - 1) + 1} = \frac{3 \sqrt[]{5} + 5}{48} \cdot (\sqrt[]{5} - 1) = \frac{5 + \sqrt[]{5}}{24} . \end{matrix}

2. A labda térfogata számítható az a) részben alkalmazott szétdarabolás mintájára is, mint

20

db szabályos hatoldalú és

12

db szabályos ötoldalú gúla térfogatának összege. Ezek oldaléle egyenlő, ti. a labda csúcsainak a származtató ikoszaéder középpontjától való távolsága, az ötoldalú gúlák magassága azonban nagyobb a hatoldalúakénál, mert az egységnyi oldalú ötszög köré írt kör sugara kisebb, mint a hatszög köré írt köré. (A hatoldalú gúlák magassága az a) részben felhasznált

d

távolságnak,

I

beírt gömbje sugarának

3

-szorosa.) Ez a számolás bonyolultabb.