Feladat:	1543. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Balogh J. ,  Berkes Z. ,  Bulkai T. ,  Csörgei J. ,  Draschitz R. ,  Gegesy F. ,  Horváth Sándor ,  Katona V. ,  Lublóy L. ,  Mészáros J. ,  Mitrocsák Anikó ,  Péceli G. ,  Péli Katalin ,  Perémy G. ,  Rácz Éva ,  Sulyok Elza ,  Takács L. ,  Varga Gabriella ,  Vetier A. ,  Zambó Péter
Füzet:	1968/január, 16 - 18. oldal		PDF  |  MathML
Témakör(ök):	Egyenesek egyenlete, Kör egyenlete, Szinusztétel alkalmazása, Koszinusztétel alkalmazása, Szabályos sokszögek geometriája, Feladat, Trigonometriai azonosságok
Hivatkozás(ok):	Feladatok: 1967/május: 1543. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.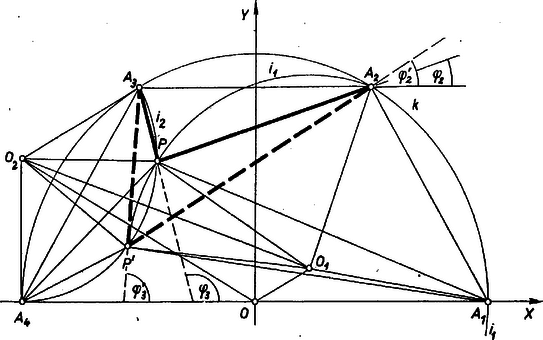   I. megoldás. A keresett $P$ pont az $A_1{A}_2$ szakasz ${40}^{\circ }$ nyílású látókörívpárjának az $A_3{A}_4$ szakasz ${120}^{\circ }$ nyílású látókörívpárjával közös pontja. Elég venni azonban az ívpárokból azt az ívet, amely a szakasznak azon a partján van, mint az $A_1{A}_2{A}_3{A}_4=N$ négyszög, hiszen a ${120}^{\circ }$-os íveket az $A_1{A}_2$ egyenestől elválasztja a vele párhuzamos $A_{3}O$ egyenes ‐ ahol $O$ a szabályos hatszög középpontja, másrészt a ${40}^{\circ }$-os ív benne van a hatszög $k$ körülírt körében ‐ hiszen az utóbbinak pontjaiból $A_1{A}_2$ látószöge csupán ${30}^{\circ }$, a ${120}^{\circ }$-os ívpárnak $N$-en kívüli tagja viszont $k$-n is kívül van, mert az $A_3{A}_4$ ív pontjaiból ${150}^{\circ }$ a látószög. A megtartott $i_1$, $i_2$ látókörívek az ábra szerint két pontban metszik egymást, legyenek ezek $P$ és $P\text{'}$ úgy, hogy $P{A}_3<P\text{'}{A}_3$, legyen $i_1$, $i_2$ középpontja $O_1$, ill. $O_2$. Az $A_{2}P{A}_3$ látószög céljára kiszámítjuk a $P{A}_2{A}_3$ háromszög másik két szögét. ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle P{A}_3{A}_2\sphericalangle }& {\displaystyle =A_4{A}_3{A}_2\sphericalangle -A_4{A}_{3}P\sphericalangle ={120}^{\circ }-A_4{O}_{2}P\sphericalangle /2=}\hfill & \text{(<mn>1</mn>)}\\ \hfill {\displaystyle }& {\displaystyle ={120}^{\circ }-\left(A_4{O}_{2}O\sphericalangle +O{O}_2{O}_1\sphericalangle +O_1{O}_{2}P\sphericalangle \right)/2.}\hfill \\ \hfill {\displaystyle P{A}_2{A}_3\sphericalangle }& {\displaystyle =A_1{A}_2{A}_3\sphericalangle -A_1{A}_{2}P\sphericalangle ={120}^{\circ }-A_1{O}_{1}P\sphericalangle /\mathrm{2,}}\hfill & \text{(<mn>2</mn>)}\end{array}}$ az utolsó szögön a $P\text{'}$ pontot tartalmazó konkáv szög értendő: $\begin{array}{c}{\displaystyle A_1{O}_{1}P\sphericalangle =A_1{O}_{1}O\sphericalangle +O{O}_1{O}_2\sphericalangle +O_2{O}_{1}P\sphericalangle \mathrm{.}}\end{array}$ A felhasználandó szögeket az $O{O}_2{A}_4$, $O{O}_1{O}_2$, $O_1{O}_{2}P$ és $O{O}_1{A}_1$ háromszögekből számítjuk. $O{O}_2{A}_4$ derékszögű háromszög, mert $i_2$ kiegészítő ívéről $i_2$-t ${60}^{\circ }$-os szögben látni, és ugyanakkora az $A_3{A}_{4}O\sphericalangle$, ezért $A_{4}O$ érinti $i_2$-t. Továbbá $A_{4}O{O}_2\sphericalangle ={30}^{\circ }$, mert $A_3{A}_4$ a $k$ és $i_2$ közös húrja, így $A_4{O}_{2}O\sphericalangle ={60}^{\circ }$. A szabályos hatszög oldalát $a$-val jelölve $O_2{A}_4=O_{2}P=a/\sqrt[]{3}=0\mathrm{,}5774a$, $O_{2}O=2a/\sqrt[]{3}$. Az $O{O}_1{A}_1$ háromszögben $O$-nál ${30}^{\circ }$-os, $O_1$-nél ${180}^{\circ }-A_1{O}_1{A}_2\sphericalangle /2={180}^{\circ }-A_{1}P{A}_2\sphericalangle ={140}^{\circ }$-os szög van, tehát $O{A}_1{O}_1\sphericalangle ={10}^{\circ }$, így $O{O}_1=a\text{sin}{10}^{\circ }/\text{sin}{40}^{\circ }=0\mathrm{,}2701a$, $A_1{O}_1=P{O}_1=a/2\text{sin}{40}^{\circ }=0\mathrm{,}7779a$.   $O_{1}O{O}_2\sphericalangle ={120}^{\circ }$, így a koszinusz‐tétellel $O_1{O}_2=1\mathrm{,}311a$, a szinusz‐tétellel $O{O}_1{O}_2\sphericalangle =49\mathrm{,}{72}^{\circ }$, és így $O{O}_2{O}_1\sphericalangle =10\mathrm{,}{28}^{\circ }$.   Az $O_1{O}_{2}P$ háromszög szögeit a félszög‐képletekkel számítjuk az oldalakból: $O_2{O}_{1}P\sphericalangle =12\mathrm{,}{64}^{\circ }$, $O_1{O}_{2}P\sphericalangle =17\mathrm{,}{14}^{\circ }$ (vagy a koszinusz‐tétel alapján). Eredményeinket beírva (1)-be és (2)-be $\begin{array}{c}{\displaystyle A_{2}P{A}_3\sphericalangle ={180}^{\circ }-P{A}_2{A}_3\sphericalangle -P{A}_3{A}_2\sphericalangle ={180}^{\circ }-18\mathrm{,}{82}^{\circ }-76\mathrm{,}{29}^{\circ }=\mathrm{84,}{49}^{\circ }\mathrm{.}}\end{array}$ $P\text{'}$ a $P$-nek tükrös párja $O_1{O}_2$-re, ezért az innen vett látószög céljára az $O_1{O}_{2}P$ és az $O_2{O}_{1}P$ szöget hozzáadás helyett kivonjuk: $A_{2}P\text{'}{A}_3\sphericalangle =55\mathrm{,}{11}^{\circ }$.   A dolgozatok többsége koordináta‐geometriai úton oldotta meg a feladatot (ahogyan az országos felmérésben, az ún. háromszögelésben is a pontokat koordinátáikkal tekintik meghatározottnak). Ilyen a következő.   II. megoldás (vázlat). Legyen a derékszögű koordinátarendszer $X$-tengelye az $A_4{A}_1$ egyenes, origója az $A_4{A}_1$ szakasz felezőpontja, hosszúságegysége az $O{A}_1$ szakasz. A fenti jelöléseket tovább is használjuk. $O{O}_1$ egyenlete $y=x\cdot \text{tg }{30}^{\circ }$, $A_1{O}_1$ egyenlete $y=\left(x-1\right)\cdot \text{tg}\left(-{10}^{\circ }\right)$, ezek metszéspontjaként $O_1$ koordinátái 3 tizedes pontossággal: ($0\mathrm{,}234$; $0\mathrm{,}135$), és az $i_1$-et tartalmazó kör egyenlete: $\begin{array}{c}{\displaystyle {\left(x-0\mathrm{,}234\right)}^2+{\left(y-0\mathrm{,}135\right)}^2=0\mathrm{,}6051.}\end{array}$ Hasonlóan az $i_2$-t tartalmazó kör egyenlete: $\begin{array}{c}{\displaystyle {\left(x+1\right)}^2+{\left(y-1/\sqrt[]{3}\right)}^2=1/3.}\end{array}$ Metszéspontjaik koordinátái: $\begin{array}{c}{\displaystyle P\left(-0\mathrm{,}\mathrm{432,}0\mathrm{,}551\right)\mathrm{,}P\text{'}\left(-0\mathrm{,}\mathrm{538,}0\mathrm{,}231\right)\mathrm{,}}\end{array}$ Másrészt $\begin{array}{c}{\displaystyle A_2\left(0\mathrm{,}\mathrm{5,}0\mathrm{,}866\right)\mathrm{,}{A}_3\left(-0\mathrm{,}\mathrm{5,}0\mathrm{,}866\right)\mathrm{,}}\end{array}$ így a keresett pontból az előírt pontokba mutató félegyenes iránytangense, majd irányszöge $P{A}_3$ esetén $\begin{array}{c}{\displaystyle \text{tg }{\phi }_3=\frac{0\mathrm{,}866-0\mathrm{,}551}{-0\mathrm{,}500+0\mathrm{,}432}=-\frac{0\mathrm{,}315}{0\mathrm{,}077}=-4\mathrm{,}\mathrm{09,}{\phi }_3=103\mathrm{,}{7}^{\circ }\mathrm{.}}\end{array}$ Hasonlóan $P{A}_2$ irányszöge ${\phi }_2=18\mathrm{,}{9}^{\circ }$, ezekből $A_{2}P{A}_3\sphericalangle ={\phi }_3-{\phi }_2=84\mathrm{,}{8}^{\circ }$, másrészt $P\text{'}$ esetére $A_{2}P\text{'}{A}_3\sphericalangle =\phi {\text{'}}_3-\phi {\text{'}}_2=86\mathrm{,}{6}^{\circ }-31\mathrm{,}{4}^{\circ }=55\mathrm{,}{2}^{\circ }$.   Zambó Péter (Miskolc, Földes F. g. II. o. t.) Horváth Sándor (Budapest, I. István g. III. o. t.)   III. megoldás. Az I. megoldás szerint $P$ az $N$ belsejében van, így az egymás utáni oldalak $P$-ből vett látószögeinek összege ${360}^{\circ }$. Legyen $A_{2}P{A}_3\sphericalangle =x$, továbbá $P{A}_3{A}_4\sphericalangle =y$; ekkor $A_{4}P{A}_1\sphericalangle ={360}^{\circ }-\left({40}^{\circ }+x+{120}^{\circ }\right)={200}^{\circ }-x$, $P{A}_4{A}_3\sphericalangle ={60}^{\circ }-y$, $P{A}_4{A}_1\sphericalangle =y$, $P{A}_1{A}_4\sphericalangle =x-{20}^{\circ }-y$, másrészt $P{A}_3{A}_2\sphericalangle ={120}^{\circ }-y$, $P{A}_2{A}_3\sphericalangle ={60}^{\circ }+y-x$, $P{A}_2{A}_1\sphericalangle =x+{60}^{\circ }-y$. A $P{A}_1{A}_2$ és $P{A}_1{A}_4$ háromszögekből a színusz‐tétel, majd az addíció‐tétel alapján kifejezhetjük $y$-t; ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{\text{sin}P{A}_2{A}_1\sphericalangle }{\text{sin}{A}_{2}P{A}_1\sphericalangle }=\underline{\frac{\text{sin}\left(x+{60}^{\circ }-y\right)}{\text{sin}{40}^{\circ }}}=\frac{P{A}_1}{A_2{A}_1}=\frac{2\cdot P{A}_1}{A_4{A}_1}=\frac{2\text{sin}P{A}_4{A}_1\sphericalangle }{\text{sin}{A}_{4}P{A}_1\sphericalangle }=}\hfill \\ \hfill {\displaystyle \phantom{MMMMMMMMMMMMMMn}=\underline{\frac{2\text{sin}y}{\text{sin}\left({200}^{\circ }-x\right)}}\mathrm{,}\text{ vagyis}}\hfill \\ \hfill {\displaystyle \frac{\text{sin}\left(x+{60}^{\circ }-y\right)}{\text{sin}y}=\text{sin}\left(x+{60}^{\circ }\right)\text{ ctg }y-\text{cos}\left(x+{60}^{\circ }\right)=\frac{2\text{sin}{40}^{\circ }}{\text{sin}\left({200}^{\circ }-x\right)}\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{ctg}y=\text{ctg}\left(x+{60}^{\circ }\right)+\frac{2\text{sin}{40}^{\circ }}{\text{sin}\left({200}^{\circ }-x\right)\text{sin}\left(x+{60}^{\circ }\right)}\mathrm{.}}\hfill & \text{(<mn>3</mn>)}\end{array}}$ Másrészt hasonlóan a $P{A}_4{A}_1$ és $P{A}_4{A}_3$ háromszögekből ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{\text{sin}P{A}_1{A}_4\sphericalangle }{\text{sin}{A}_{1}P{A}_4\sphericalangle }=\underline{\frac{\text{sin}\left(x-{20}^{\circ }-y\right)}{\text{sin}\left({200}^{\circ }-x\right)}}}& {\displaystyle =\frac{P{A}_4}{A_1{A}_4}=\frac{P{A}_4}{2\cdot A_3{A}_4}=\frac{\text{sin}y}{2\text{sin}{120}^{\circ }}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\underline{\frac{\text{sin}y}{\sqrt[]{3}}}\mathrm{,}\text{ vagyis}}\hfill \\ \hfill {\displaystyle \frac{\text{sin}\left[\left(x-{20}^{\circ }\right)-y\right]}{\text{sin}y}=\text{sin}\left(x-{20}^{\circ }\right)\text{ctg}}& {\displaystyle y-\text{cos}\left(x-{20}^{\circ }\right)=\frac{\text{sin}\left({200}^{\circ }-x\right)}{\sqrt[]{3}}\mathrm{,}}\hfill \end{array}}$ amiből, felhasználva, hogy $\text{sin}\left({200}^{\circ }-x\right)=-\text{sin}\left({20}^{\circ }-x\right)=\text{sin}\left(x-{20}^{\circ }\right)$, $\begin{array}{c}{\displaystyle \text{ctg}y=\text{ctg}\left(x-{20}^{\circ }\right)+\frac{1}{\sqrt[]{3}}\mathrm{.}}\end{array}$ (4) (3)és (4) jobb oldalából az első tagok különbsége $\begin{array}{c}{\displaystyle \text{ctg}\left(x+{60}^{\circ }\right)-\text{ctg}\left(x-{20}^{\circ }\right)=\frac{\text{sin}\left[\left(x-{20}^{\circ }\right)-\left(x+{60}^{\circ }\right)\right]}{\text{sin}\left(x+{60}^{\circ }\right)\text{sin}\left(x-{20}^{\circ }\right)}=\frac{-\text{sin}{80}^{\circ }}{\text{sin}\left(x+{60}^{\circ }\right)\text{sin}\left(x-{20}^{\circ }\right)}\mathrm{,}}\end{array}$ a nevező azonos (3) második tagja nevezőjével és a $2\text{sin}u\text{sin}v=\text{cos}\left(u-v\right)-\text{cos}\left(u+v\right)$ azonosság felhasználásával így alakul: $\left[\text{cos}{80}^{\circ }-\text{cos}\left(2x+{40}^{\circ }\right)\right]/2$, ezért (3) és (4) különbségéből ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{4\text{sin}{40}^{\circ }-2\text{sin}{80}^{\circ }}{\text{cos}{80}^{\circ }-\text{cos}\left(2x+{40}^{\circ }\right)}=\frac{1}{\sqrt[]{3}}\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{cos}\left(2x+{40}^{\circ }\right)=\text{cos}{80}^{\circ }-4\sqrt[]{3}\text{sin}{40}^{\circ }\left(1-\text{cos}{40}^{\circ }\right)=-0\mathrm{,}\mathrm{8682,}}\hfill \\ \hfill {\displaystyle 2x+{40}^{\circ }={180}^{\circ }\pm 29\mathrm{,}{74}^{\circ }\mathrm{,}}\hfill \\ \hfill {\displaystyle x_1=84\mathrm{,}{87}^{\circ }\mathrm{,}{x}_2=55\mathrm{,}{13}^{\circ }\mathrm{.}}\hfill \end{array}}$ Sulyok Elza (Nagybátony‐Bányaváros, Gimn., II. o. t.)