Feladat: 1542. matematika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Füzet: 1968/november, 102 - 105. oldal  PDF  |  MathML 
Témakör(ök): Magasságpont, Párhuzamos szelők tétele, Diszkusszió, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):Feladatok: 1967/május: 1542. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) Ismeretes, hogy az ABC háromszög 3 oldalegyenese és 3 magasságegyenese felezi az A'B'C' talpponti háromszög belső és külső szögeit ‐ természetesen amennyiben a talpponti háromszög létrejön, vagyis ha az eredeti háromszög nem derékszögű. Pontosabban: hegyesszögű háromszög talpponti háromszögének belső szögeit a 3 magasságegyenes felezi (ennélfogva a rájuk rendre merőlegesen álló oldalegyenesek a külső szögeket felezik), tompaszögű háromszög talpponti háromszögében a tompaszöget alkotó 2 oldalegyenes és a tompaszög csúcsából kiinduló magasság játsszák a belső szögfelezők szerepét (1. a, b, c ábra, az A'B'C' háromszög beírt körének középpontja rendre M, a tételben kiemelt A csúcs, il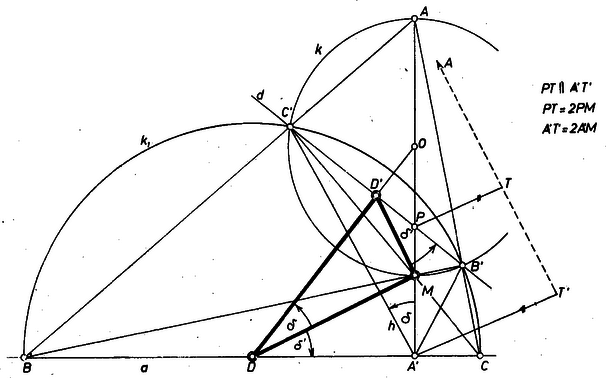l. C).

 

 

1.a. ábra
 

Tekintsük az A'A szögfelezővel kettévágott talpponti háromszögnek C'A'P részháromszögét, és alkalmazzuk ennek C'-ből kiinduló C'M és C'A szögfelezőire a szögfelezők osztásarányára vonatkozó tételt (1. a és b ábra, csupán A és M külső, ill. belső szerepe cserélődik fel):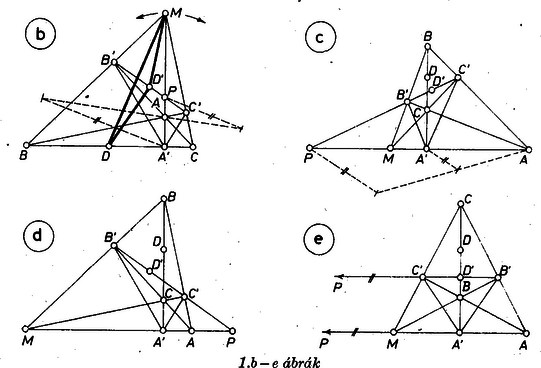
A'MPM=A'C'PC'=A'APA.
 

 


A két szélső arány egybevetéséből rendezéssel kapjuk (1)-et. Ugyanez az 1. c és 1. d ábra esetében is érvényes, itt a C'A'P, ill. a B'A'P háromszög magában tartalmazza a talpponti háromszöget. Ezzel az állítást bebizonyítottuk. (Ha P nem jön létre (pl. 1. e ábra), mert B'C'⊥BC, tehát B'C'∥AA', akkor az állítás tárgytalan.)
A kívánt szerkesztés céljára megállapítjuk, hogy M és A egyike az A'P szakaszon van ‐ ti. közülük a belső szögfelezőn levő pont ‐, másika pedig az A'P szakasz meghosszabbításán, ennélfogva fordítva is, az A', P pontpár egyike belső pontja az AM szakasznak, másika pedig e szakasz meghosszabbításán van.
b) Az (1) alapján adandó szerkesztésben ‐ az 1447. feladat betűzését megtartva ‐ a BC és a B'C' oldal D, ill. D' felezőpontját tekintjük adottnak. Az ottani I. és II. megoldásból felhasználjuk, hogy egyrészt B'C'⊥DD', másrészt hogy MDC és MD'B' hasonló háromszögek, és megfelelő csúcsaik egymás utáni körüljárásában az irány egymással ellentétes, ezért a DM félegyenest DC-be átvivő elfordulás egyenlő és ellentétes irányú a D'M-et D'B'-be átvivő elfordulással.
2. Ezek alapján megrajzoljuk a B'C'=d egyenest, ebből a közte és MD' között levő szög átmásolásával a BC=a egyenest, és ekkor az M-ből a-ra állított merőleges, az AA' magasságegyenes, kimetszi B'C'-ből P-t, BC-ből A'-t.
Ezután az A', P, M ponthármashoz megszerkesztjük az (1)-nek eleget tevő A pontot, figyelembe véve a négy pont kölcsönös helyzetéről fent mondottakat.
Az A pont meghatározását megkönnyíti a következő észrevétel: az ABC háromszögben az AM és a BC szakaszok fölé rajzolt k, k1 Thalész-körök átmennek a B', C' pontokon, így centrálisuk nem más, mint a B'C' közös húr felező merőlegese, vagyis a DD' egyenes. Emiatt a DD' egyenes az A'M egyenest az AM szakasz O felezőpontjában metszi.
Legyen DD' és A'M metszéspontja O, és az O középpontú, M-en átmenő kör k, ebben M-nek átellenes pontja A. k-nak d-vel alkotott metszéspontjait tetszőleges sorrendben B'-nek, C'-nek véve, kapjuk az AB', AC' oldalegyeneseket, melyekből az MC', MB' magasságvonalak metszik ki a C, B csúcsokat.
Mivel k1-ben BC átmérő, B'C' húr, így BC>B'C', és az MBC, MB'C' háromszögek hasonlósága miatt MD>MD' következik. Ez tehát a szerkeszthetőség szükséges feltétele. Ez a feltétel nem zárja ki M és D' egybeesését, amikor ‐ mint azt korábbi megoldásainkban láttuk ‐ derékszögű háromszöget kapunk, végtelen sok megoldás van.
Szerkesztésünk helyességének a vizsgálatánál feltesszük, hogy D, D', M különböző pontok, és MD>MD', továbbá hogy M nincs rajta a DD' egyenesen. Ekkor szerkesztésünk szerint a d és a egyenesek meghatározhatók. Ha M a d egyenesen van, akkor a is átmegy M-en szerkesztésünk szerint, és A', valamint P azonos M-mel. Az A'M egyenesnek ebben az esetben az M-ben a-ra emelt merőleges felel meg, és mivel az a=MD egyenes nem merőleges DD'-re, O ebben az esetben is meghatározható.
Ha M nincs rajta d-n, akkor az a-n levő A' vetülete M-től különböző pont. Megmutatjuk, hogy az a forgatás, mely a DM egyenest DD'-be viszi, az A'M egyenest MD'-vel párhuzamos h helyzetbe viszi. Valóban, MD-t először D körül δ-val elforgatva D'D-be jutunk, majd 90∘-kal elforgatva d-be, végül δ'-vel elforgatva MD'-be. Ha e három forgatást más sorrendben hajtjuk végre, nevezetesen MD-t először δ'-vel forgatjuk el, akkor a-t kapjuk, majd 90∘-kal elforgatva kapjuk MA'-t, végül ezt az egyenest δ-val forgatva kapjuk h-t. E három forgatás végeredménye ‐ irány szempontjából ‐ nem függ sorrendjüktől, tehát h párhuzamos MD'-vel, vagyis az A'M egyenest M körül δ-val elforgatva az MD' egyenest kapjuk. Mivel a δ=MDD'∢ kisebb a DD'M szögnél (hiszen MD'<MD), az A'M egyenes a DD' egyenest a D'-n túli meghosszabbításában metszi. Így az O pont mindig létrejön, és D' az OD szakaszon van.
Az MOD' háromszög D'-nél levő szöge a DD'M háromszög külső szöge, így nagyobb az MDD', és az azzal egyenlő OMD' szögnél, ezért az MOD' háromszögben MO-val szemben nagyobb szög van, mint D'O-val szemben ezért MO>D'O, tehát D' a k belsejében van, a B', C' metszéspontok valóban létrejönnek.
Ha M és A egyike sem azonos a B', C' pontokkal, akkor az AB', MC' egyenesek meg vannak határozva két-két pontjukkal, és nem párhuzamosak, hiszen B', C' nem lehetnek k átellenes pontjai, így C létrejön, és hasonlóan bizonyítható B létezése is.
A kapott ABC háromszögben BB', CC' magasságvonalak, M tehát magasságpont és AM⊥BC, BC∥A'D. A BC szakasz D* felezőpontja elemzésünk szerint az OD' egyenesen van, hiszen ez k és k1 centrálisa, és MBC, MB'C' hasonlósága, valamint szerkesztésünk miatt MD∥MD*, azaz D* az MD egyenesen is rajta van. Eszerint D* azonos az OD', MD egyenesek közös pontjával, D-vel, tehát ABC a keresett háromszög.
Ha M a B', C' pontok egyikével, mondjuk B'-vel azonos, akkor C is azonos M-mel, és B-t az MD, AC' egyenesek metszéspontja adja. Ebben az esetben C-nél derékszög van, és M valóban magasságpont, D, D' pedig az előírt szakaszokat felezik.
Ha A azonos a B', C' egyikével, akkor feladatunknak nincs megoldása.
Végül, ha M a DD' egyenesen van, akkor O nem jön létre, így A-t közvetlenül (1) alapján kell megszerkesztenünk: ha M a DD' szakaszon van, a DD' fölé rajzolt k2 Thalész-kört a DD'-re M-ben emelt merőleges messe az U, V pontokban, ekkor a k2 kör U és V-beli érintőinek a metszéspontja lesz A; ha pedig M a DD' szakasz meghosszabbításán van, akkor az M-ből k2-höz húzott érintők érintési pontja lesz U és V, és DD'-ből az UV egyenes metszi ki A-t. A szerkesztés további lépései, és a szerkesztés helyességének a bizonyítása ennek megfelelően módosul.