Kezdőlap


Feladat:	1541. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Andor Cs. , Balogh József , Berács J. , Bulkai Tamás , Dombi J. , Draschitz Rudolf , Farkas Gy. , Kocsis Ferenc , Koren András , Lempert László , Mérő L. , Mészáros József , Moson Péter , Nagy Zs. , Pintz János , Somos Endre , Takács László , Tátray Péter , Vetier András
Füzet:	1969/április, 145 - 148. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül négyszögekben, Síkgeometriai számítások trigonometriával, Párhuzamos szelők tétele és megfordítása, Feladat
Hivatkozás(ok):	Feladatok: 1967/május: 1541. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Megmutatjuk, hogy minden $A B C D = N$ konvex négyszöghöz van kívánt tulajdonságú $e$ egyenes. Legyen $N$ tükörképe az $M$ pontra az $A' B' C' D' = N'$ négyszög. Ha $A M = M C$ , akkor az $A C$ átló egyenese megfelel $e$ -nek; mindkét szemközti oldalpárral való metszéspontja $A$ és $C$ , így a feladat állítása is nyilvánvalóan teljesül.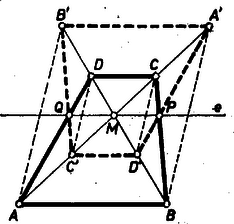
Ha még $B M = M D$ is teljesül, akkor $N$ paralelogramma, minden, az $M$ -en átmenő egyenes megfelel $e$ -nek és világos, hogy mindre teljesül a feladat állítása. Ha $B M \neq M D$ , akkor $B'$ és $D'$ közül egyik $N$ belsejében van, a másik rajta kívül, ezért $N'$ határának $A B' C$ és $C D' A$ része közül egyik a végpontjaitól eltekintve $N$ belsejében van, a másik rajta kívül, így $A C$ -n kívül nincs más, $e$ -nek megfelelő egyenes.
Vizsgáljuk a továbbiakban azt az esetet, ha $M$ egyik átlót sem felezi. Válasszuk a betűzést úgy, hogy $A M > C M$ és $B M > D M$ teljesüljön. Ekkor $C'$ , $D'$ , s így az egész köztük levő szakasz $N$ -ben van, az $A' B'$ szakasz $N$ -en kívül van. Az $A' D'$ szakasz metszi a $B C$ szakaszt egy $P$ pontban, mert az $A' B' D'$ háromszög tartalmazza $C$ -t, $B$ viszont a $B' D'$ oldal meghosszabbításán van, $A' B'$ pedig, mint láttuk, $N$ -en kívül (1. ábra).

1. ábra

P

tükörképe,

Q

, rajta van

N'

-n, mert

P

N

-en van, és mivel

P

N'

-n is rajta van, az a pont, aminek ő a tükörképe, vagyis

Q

, rajta van

N

-en is. A

P Q

egyenes tehát alkalmas

e

-nek, és ez az egyetlen ilyen, mivel

P

-n és

Q

-n kívül nincs

N

és

N'

kerületének közös pontja.
Azt kell tehát bizonyítanunk, hogy ha

P Q

metszi az

A B

C D

oldalak egyikét, akkor metszi a másikat is, és a metszéspontok egymás tükörképei

M

-re.

e

csak akkor nem metszi pl.

C D

-t, ha párhuzamos vele. Megmutatjuk, hogy ez csak úgy lehetséges, ha

e

A B

-t sem metszi, azaz ha ezzel is párhuzamos. Tegyük fel, hogy

C D ∥ P Q

, és alkalmazzuk a párhuzamos szelők tételét a

C A D

és

C B D

szögekre (1. ábra):

\begin{matrix} \frac{C A}{M A} = \frac{C D}{M Q} = \frac{D C}{M P} = \frac{D B}{M B}, \end{matrix}

a szélső arányokból

1

-et‐

1

-et levonva

\begin{matrix} \frac{C A}{M A} - 1 = \frac{C A - M A}{M A} = \frac{C M}{M A} = \frac{D M}{M B}, \end{matrix}

ezek a szakaszok az egymást

M

-ben metsző

A C

B D

egyeneseken feküsznek, így valóban

C D ∥ A B

, tehát

P Q ∥ A B

, amint állítottuk.
Itt nem használtuk fel az átlók részeinek nagyságviszonyára vonatkozó fentebbi feltevéseket, ezért bizonyításunk az

A B ∥ P Q

és

M P = M Q

feltevésből kiindulva is érvényes. Ezzel a feladat állításának első részét bebizonyítottuk.
Azt is kaptuk, hogy ha a mondott

P Q

egyenes nem metszi az

A B

C D

egyenesek egyikét, akkor

N

trapéz (és a tett korlátozás folytán

A B \neq C D

). Fordítva, ha

A B ∥ C D

és

A B \neq C D

, akkor

P Q ∥ A B

. Ugyanis az

A B A' B'

és

C' D' C D

paralelogrammák hasonló helyzetűek az

M

középpontra vonatkozóan, így

B A' C D'

trapéz, és az átlóinak

P

, valamint szárainak

M

metszéspontját összekötő

e

egyenes felezi a

B A'

C D'

alapokat, tehát az előbbi paralelogrammáknak középvonala.
Eszerint ha

N

nem trapéz, akkor

A B

és

C D

metszik egymást egy

T

pontban, másrészt

P Q

metszi

A B

-t,

C D

-t egy

R

, ill.

S

pontban, és azt kell megmutatnunk, hogy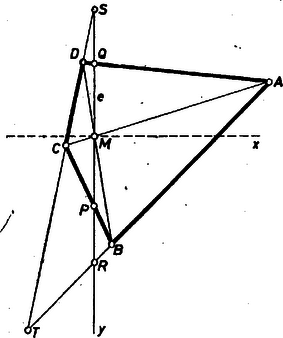

M R = M S

2. ábra

Felhasználjuk a következő, alább bebizonyítandó segédtételt: Ha a sík egymást

O

-ban metsző

f

és

g

egyenesét a

H

-n átmenő

h_{0}

h_{1}

h_{2}

egyenesek rendre az

F_{0}

F_{1}

F_{2}

, ill.

G_{0}

G_{1}

G_{2}

pontban metszik (3. ábra), más kifejezéssel: ha a

g

egyenes

O

G_{0}

G_{1}

G_{2}

pontnégyesét a

H

pontból az

f

egyenes

O

F_{0}

F_{1}

F_{2}

pontnégyesébe vetítjük át, akkor

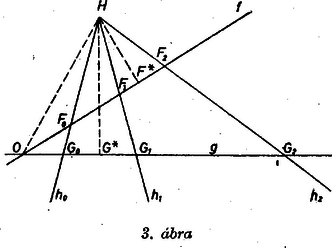\begin{matrix} \frac{O G_{1}}{G_{1} G_{0}} : \frac{O G_{2}}{G_{2} G_{0}} = \frac{O F_{1}}{F_{1} F_{0}} : \frac{O F_{2}}{F_{2} F_{0}} . \end{matrix}

(1)

Ezt kétszer alkalmazzuk;

O

G_{0}

G_{1}

G_{2}

szerepére mindkétszer a

C D

egyenesnek rendre

S

D

C

T

pontját választjuk;

f

-ként mindkétszer

e

-t vesszük, de

H

szerepére először

A

-t, másodszor

B

-t választjuk; így

F_{0}

F_{1}

F_{2}

helyére először

Q

M

R

lép, másodszor

M

P

R

, tehát

\begin{matrix} \frac{S C}{C D} : \frac{S T}{T D} = \frac{S M}{M Q} : \frac{S R}{R Q} = \frac{S P}{P M} : \frac{S R}{R M} . \end{matrix}

Az utóbbi két arány egyenlőségéből,

P M = M Q

felhasználásával, majd a szakaszok hosszát csupa

M

-ből induló szakasszal kifejezve, beszorozva, egyszerűsítve

\begin{matrix} S M \cdot R Q = S P \cdot R M, \\ M S (M R + M Q) = (M S + M P) \cdot M R, \\ M S = M R, q u . e . d . \end{matrix}

Visszatérve a segédtétel bizonyítására, szorozzuk meg (1) első tagjának számlálóját is, nevezőjét is

{H G}^{*}

-gal, ahol

G^{*}

H

pont vetülete

g

-n, majd a szorzatokat ‐ mint a

H O G_{1}

, ill.

H G_{1} G_{0}

háromszög területe mértékszámának

2

-szeresét ‐ fejezzük ki e háromszögek

H

-ból induló oldalaival és a köztük levő szöggel:

\begin{matrix} \frac{O G_{1}}{G_{1} G_{0}} = \frac{O G_{1} \cdot H G^{*}}{G_{1} G_{0} \cdot H G^{*}} = \frac{2 \cdot H O G_{1}}{2 \cdot H G_{1} G_{0}} = \\ = \frac{H O \cdot H G_{1} sin O H G_{1} ∢}{H G_{1} \cdot H G_{0} sin G_{1} H G_{0} ∢} = \frac{H O sin O H G_{1} ∢}{H G_{0} sin G_{1} H G_{0} ∢} . \end{matrix}

Ebből (1) második tagjának hasonló alakítását az

1

-es index

2

-esre cserélésével kapjuk, a 3. és 4. tagéit pedig az első kettőből a

G

betűknek

F

-re cserélésével, ami által kellő egyszerűsítések után (1) a nyilvánvalóan igaz

\begin{matrix} \frac{sin O H G_{1} ∢}{sin G_{1} H G_{0} ∢} : \frac{sin O H G_{2} ∢}{sin G_{2} H G_{0} ∢} = \frac{sin O H F_{1} ∢}{sin F_{1} H F_{0} ∢} : \frac{sin O H F_{2} ∢}{sin F_{2} H F_{0} ∢} \end{matrix}

egyenlőségbe megy át.

Takács László (Sopron, Széchenyi I. Gimn.) és
Mészáros József (Makó, József A. Gimn.)
dolgozatainak felhasználásával és kiegészítésekkel

II. megoldás (vázlat). Az állítás második részét koordináta-geometriai úton bizonyítjuk, támaszkodva az I. megoldás azon részeire, amelyek szerint az

e = P Q

egyenes általában egyértelműen létezik.

y

tengelynek a

P Q

egyenest, origónak az

M

pontot választjuk, legyen továbbá

P

ordinátája

- p

, így

Q

-é

p

, az ezeken átmenő oldalegyenesek, valamint az átlók egyenesének egyenlete:

\begin{matrix} B C : y = b x - p, & A D : y = a x + p, \\ B D : y = n x, (n \neq a, b) & A C : y = m x . (m \neq a, b) \end{matrix}

Így azt kell megmutatnunk, hogy az

y

tengely és az

A B

, ill.

C D

egyenes metszéspontja közti szakaszt

M

felezi, a két ordináta egymásnak

(- 1)

-szerese.

A D

és

A C

egyenletéből

A

abszcisszája

\begin{matrix} x_{A} = \frac{p}{m - a}, \end{matrix}

többi csúcsokét ebből az alábbi helyettesítésekkel kapjuk:

\begin{matrix} p & m & ahelyére \\ Cesetében & - p & m & blép \\ Besetében & - p & n & blép \\ Desetében & p & n & alép. \end{matrix}

Azt is mondhatjuk, hogy

D

abszcisszáját

B

-éből úgy kapjuk, hogy

p

és

b

helyére rendre

- p

-t,

a

-t írunk. Az ordináta mindig az abszcissza

m

-szerese, ill.

n

-szerese.
Általában az

L_{1} (u_{1}, v_{1})

L_{2} (u_{2}, v_{2})

pontokkal meghatározott egyenes és az

y

tengely metszéspontjának ordinátája az

\begin{matrix} y = v_{1} + \frac{v_{2} - v_{1}}{u_{2} - u_{1}} (x - u_{1}), x = 0 \end{matrix}

egyenletrendszerből:

\begin{matrix} v_{1} + \frac{v_{2} - v_{1}}{u_{2} - u_{1}} (- u_{1}) = \frac{u_{2} v_{1} - u_{1} v_{2}}{u_{2} - u_{1}} . \end{matrix}

Legyen itt

L_{1} = A

L_{2} = B

, így az

A B

oldalegyenes és a

P Q

egyenes

R

metszéspontjának ordinátája, a fentiek felhasználásával:

\begin{matrix} \frac{u_{2} m u_{1} - u_{1} n u_{2}}{u_{2} - u_{1}} = \frac{(m - n) u_{1} u_{2}}{u_{2} - u_{1}} = \frac{m - n}{\frac{1}{u_{1}} - \frac{1}{u_{2}}} = \\ = \frac{m - n}{\frac{m - a}{p} + \frac{n - b}{p}} = \frac{(m - n) p}{(m + n) - (a + b)} . \end{matrix}

Ebből könnyen megkapjuk a

C D

egyenes

y

tengelyen levő

S

pontjának ordinátáját,

A

helyére

C

-t és

B

helyére

D

-t írva, ugyanis ‐ mint láttuk ‐ eközben

p

helyére mindkét helyettesítés miatt

- p

lép, a másik helyettesítés viszont ‐ ti.

a

helyére

b

, ill.

b

helyére

a

‐ egymástól független. Így

S

ordinátája

\begin{matrix} \frac{(m - n) (- p)}{(m + n) - (b + a)}, \end{matrix}

és ez az előrebocsátott megjegyzés szerint az állítást igazolja.
Itt nem volt célunk annak elemzése, hogy a metszéspontok milyen

a

b

m

n

értékrendszerek esetén léteznek. Azt mindenesetre látjuk, hogy

S

létezésének feltételei ugyanazok, mint

R

létezésének feltételei. Ezzel teljesítettük kitűzött célunkat.