Kezdőlap


Feladat:	1540. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bajmóczy E. , Balázs D. , Balogh J. , Bán Ilona , Berács J. , Bodor I. , Bulkai T. , Csörgei J. , Dombi J. , Draschitz R. , Farkas Gy. , Fuggerth E. , Futó Ilona , Gegesy F. , Horváth S. , Joó I. , Juhász Ágnes , Katona V. , Kovács Tamás , Lakatos L. , Losonci Z. , Lublóy L. , Mészáros J. , Mitrocsák Anikó , Moson P. , Munk S. , Nagy Zs. , Orbán G. , Pál J. , Pap Márta , Papp Z. , Péli Katalin , Perémy G. , Pintér Ágnes , Pintz J. , Rácz Éva , Sulyok Elza , Szabó Klára , Takács L. , Tóth Tibor , Varga Gabriella , Vetier A. , Viszkei Gy. , Zambó Péter , Zöldy B.
Füzet:	1968/március, 106 - 107. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Numerikus módszerek, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1967/május: 1540. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a kérdéses $A B$ körív középpontja $O$ , sugara $O A = r$ , az ív és a húr hossza $i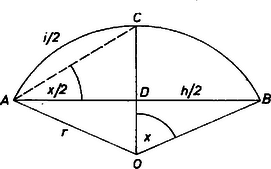$ , ill. $h$ .

A szelet

t

területe az

A O B

körcikk és az

A O B

háromszög területének különbségeként, az adatokat felhasználva

\begin{matrix} t = \frac{i r}{2} - \frac{h \sqrt[]{r^{2} - h^{2} / 4}}{2} = 5 r - 4 \sqrt[]{r^{2} - 16} . \end{matrix}

Legyen még az ív felezőpontja

C

, és

C O B ∢ = x

. Ekkor

r = h / (2 sin x)

, másrészt

i = 2 r x

(

x

-et ívmértékben véve), innen

r

kiküszöbölésével

\begin{matrix} \frac{x}{sin x} = \frac{i}{h} = \frac{5}{4}, x = \frac{5}{4} sin x . \end{matrix}

(1)

Ennek az egyenletnek közelítő megoldását fogjuk keresni.
Alsó korlátot ad

x

-re az az ismert tény, hogy

x = 60^{\circ} = π / 3

esetén

i = r \cdot 2 π / 3

h = r \sqrt[]{3}

,és

i / h = 2 π / \sqrt[]{27} < 1, 21 < 1, 25

, ugyanis az

i / h

arány a középponti szög növekedésével nő (amíg

0 < x < π / 2

), eszerint

x > 60^{\circ}

.
Felső korlátot kapunk viszont az

A C D

derékszögű háromszögből, ahol

D

A B

húr felezőpontja, ebben ugyanis

D A C ∢ = x / 2

, és az

A C

átfogó kisebb az ív felénél:

\begin{matrix} cos \frac{x}{2} = \frac{A D}{A C} > \frac{h / 2}{i / 2} = 0, 8, \frac{x}{2} < 36, 8^{\circ}, x < 73, 6^{\circ} . \end{matrix}

Próbálkozzunk e két korlát között

x = 65^{\circ}

-kal, ami radiánban

1, 1345

, (1) jobb oldala pedig

\begin{matrix} (5 / 4) \cdot sin x = (5 / 4) \cdot 0, 9063 = 1, 1229; x / sin x = 1, 252 > 1, 25. \end{matrix}

Eszerint

x < 65^{\circ}

, de jóval közelebb áll

65^{\circ}

-hoz, mint

60^{\circ}

-hoz.
Második próbaként

x = 64, 5^{\circ}

-ot véve a két oldal

1, 1257

, ill.

(5 / 4) \cdot 0, 9026 = 1, 1282

;

x / sin x = 1, 247

, ezért

x > 64, 5^{\circ}

. A kívánt

1, 25

arány a talált értékek közti (

1, 247

1, 252

) intervallumot

3 : 2

arányban osztja, ezért a

64, 5^{\circ}

és

65^{\circ}

közti intervallumot

3 : 2

arányban osztó

64, 8^{\circ}

-kal célszerű próbálkozni. Ezzel (1) mindkét oldala

1, 1310

, a táblázatunk alapján elérhető pontossággal (1) megoldása

x = 64, 8^{\circ}

.
Most már

r = h / (2 sin x) = 4, 42

hosszúságegység, és az előrebocsátottak szerint

t = 22, 1 - 4 \sqrt[]{0, 42 \cdot 8, 42} = 14, 6

területegység.

Tóth Tibor (Szolnok, Verseghy F. g. III. o. t.)
Kovács Tamás (Győr, Czuczor G. Bencés g. III. o. t.)

Megjegyzések. 1. A

(sin x) / x = 0, 8

egyenletre első közelítő értéket kapunk úgy is, hogy az iskolai függvénytáblázatban található

\begin{matrix} sin x = x - \frac{x^{3}}{6} + \frac{x^{5}}{120} - \frac{x^{7}}{5040} + ... \end{matrix}

kifejezés első

3

tagját vesszük figyelembe, az így adódó

\begin{matrix} \frac{sin x}{x} = 1 - \frac{x^{2}}{6} + \frac{x^{4}}{120} = 0, 8, x^{4} - 20 x^{2} + 24 = 0 \end{matrix}

egyenletet megoldjuk, és gyökei közül a célszerűnek látszó

\begin{matrix} x = \sqrt[]{10 - \sqrt[]{76}} \approx 1, 132 \approx 65^{\circ} \end{matrix}

-ot vesszük kiindulásul.
2. Elkerülhetjük a fok-radián táblázat használatát. Az

x_{rad} = (π / 180^{\circ}) \cdot x_{fok}

összefüggés alapján (1) így alakítható (tovább

x

-et fokban mérjük):

\begin{matrix} \frac{sin x}{x} = \frac{4 π}{900} = 0, 013963 (= c) . \end{matrix}

x = 60^{\circ}

70^{\circ}

65^{\circ}

64^{\circ}

esetén az osztás logaritmus használata nélkül is gyorsan végezhető, a hányados rendre

\begin{matrix} 0, 01443 (> c), 0, 01342 (< c), 0,013943 (< c), 0,014044 (> c) . \end{matrix}

Az utolsó kettőben a hiány és a többlet aránya

(- 0, 00020) : (+ 0, 00081) = 1 : 4

, ebből ismét

64, 8^{\circ}

adódik.